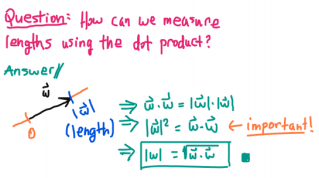#MTBoS How do you motivate the dot product for math students? I think my latest approach is my best yet!
Extend ℝ to ℝ^n. We can multiply numbers in ℝ; how might we multiply vectors in ℝ^n?
Hint: We can multiply numbers on a number line. Reduce to that. 1/
Extend ℝ to ℝ^n. We can multiply numbers in ℝ; how might we multiply vectors in ℝ^n?
Hint: We can multiply numbers on a number line. Reduce to that. 1/
Note: I don& #39;t think I& #39;ve seen the above explanation before, but @robertghrist might have some similar content in his excellent YouTube playlist on multivariable calculus. 2/
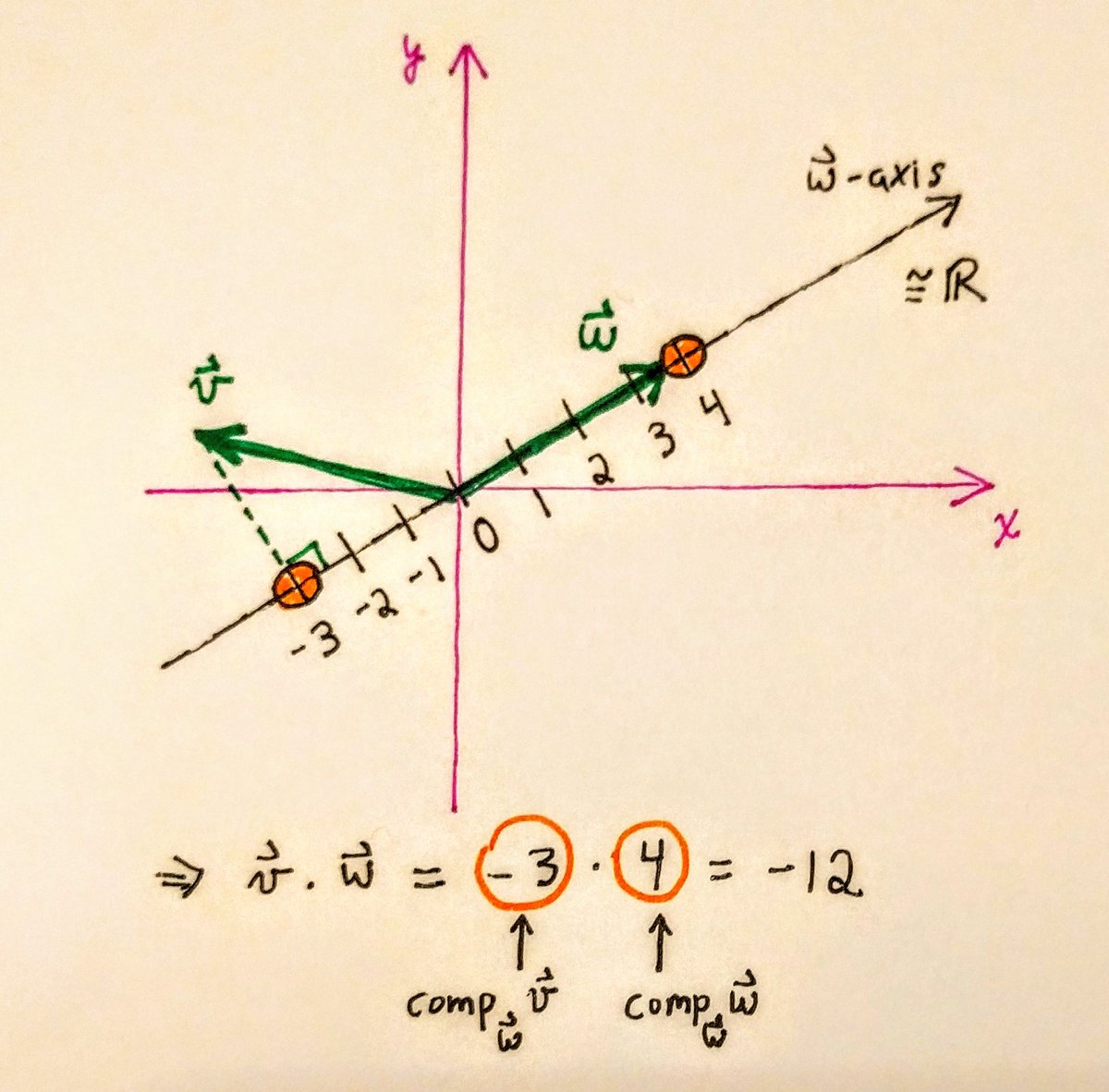
We& #39;ve decided to multiply vectors as follows. First, project both onto the same line (taking the shortest path to the line), thereby reducing the vectors to real numbers. Second, multiply those numbers as usual.
We call this the dot product!
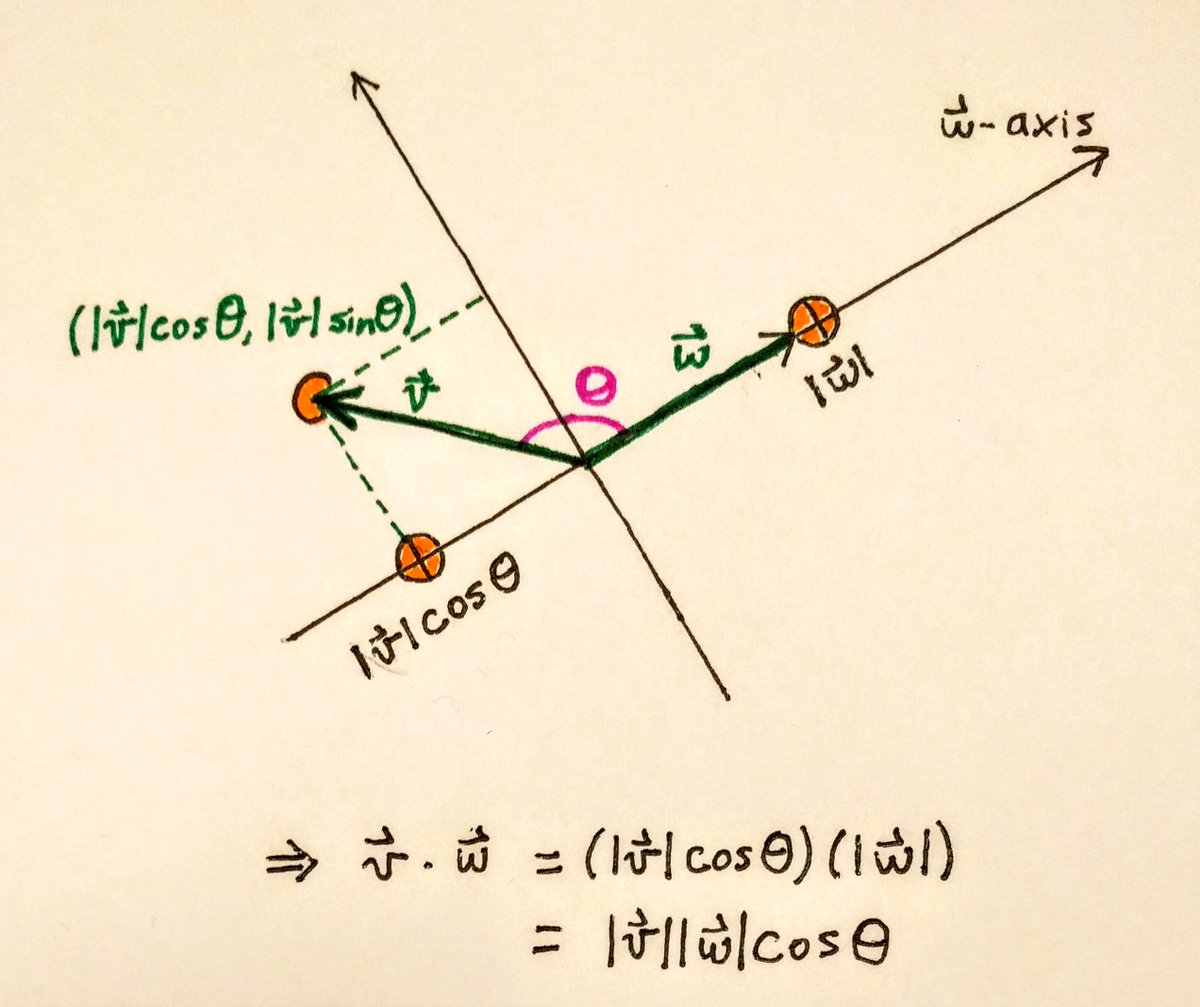
How about a general formula? 3/
We call this the dot product!
How about a general formula? 3/
So, a dot product is a product of projections. (But, how do we know whether to project onto v or w? Exercise: show that we get the same result either way!)
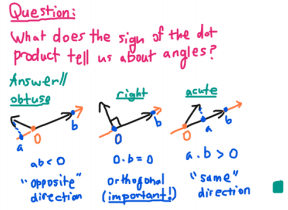
Can we use the dot product like we use real-number multiplication? For example, what does the sign tell us? 4/
Can we use the dot product like we use real-number multiplication? For example, what does the sign tell us? 4/
So, we can use the dot product to classify (and measure) angles. In fact, both types of measurements in geometry (lengths and angles) can be determined from the dot product! This is useful in all kinds of applied problems.
How could we measure lengths using the dot product? 5/
How could we measure lengths using the dot product? 5/
We& #39;re on a roll. But, the last formula would be more useful if we could compute the dot product without already knowing the lengths of the vectors and the angle between them. Is that even possible?
It should be enough to know the x-, y-, and z- components of each vector. 6/
It should be enough to know the x-, y-, and z- components of each vector. 6/
Here, I would do a very cool, modern application of our ideas to recommender systems. These are ubiquitous on the modern web, including on this platform (Twitter). I& #39;ll postpone that for now because it deserves its own thread, although I& #39;m eager to share how I found it! 7/
We& #39;ve been viewing the dot product as an extension of real-number multiplication. In fact, it does share many properties with that more familiar operation. (Here, I& #39;d develop symmetry and bilinearity, along with the multiplication table for the standard basis vectors.)
But... 8/
But... 8/
When extending concepts to new contexts, something is often lost in translation. Is there anything we can do with real-number multiplication that we can& #39;t do with the dot product? (The answer is yes, but I like to let students think about this themselves.) 9/
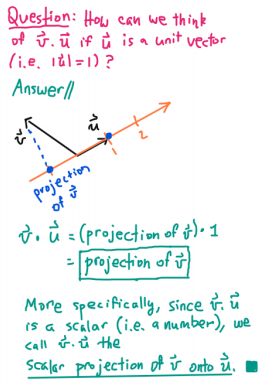
It& #39;s time to come full circle. We began with projections, and we shall end with them.
The dot product is a product of projections, but often we need to calculate a projection all by itself. How can we do this with a dot product?
Hint: What is v dot u, if u is a unit vector? 10/
The dot product is a product of projections, but often we need to calculate a projection all by itself. How can we do this with a dot product?
Hint: What is v dot u, if u is a unit vector? 10/
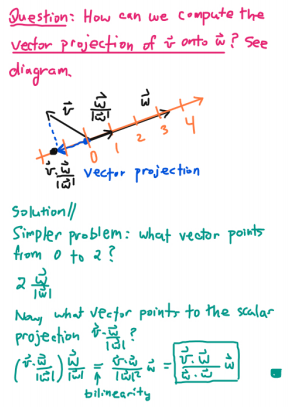
Now, say we have any two vectors v and w, where w is not necessarily a unit vector. How could we compute the projection of v onto w, using a dot product? 11/

 Read on Twitter
Read on Twitter