Thread: What is the Music of the Primes? (From last night& #39;s @MoMath1 lecture on the Riemann Hypothesis. TL;DR: watch this @QuantaMagazine video https://youtu.be/zlm1aajH6gY )
The">https://youtu.be/zlm1aajH6... tricky thing about prime numbers is that they’re defined by what they’re not. A composite number is a
The">https://youtu.be/zlm1aajH6... tricky thing about prime numbers is that they’re defined by what they’re not. A composite number is a
2/ product of two other whole numbers; for example, 28 is composite (and hence not prime) since 4 × 7 = 28. For millennia, primes have fascinated people of all ages. Even babies can understand primes! Indeed, before my oldest could talk, he enjoyed playing with a set of 20 blocks
3/ stacking them in neat rectangles of 4×5 or sometimes 2×10. One day he seemed quite upset with his blocks, unable to make a rectangle. It turned out that one of the blocks had rolled under the couch; he experimentally discovered that 19 is prime!
4/ Perhaps we should’ve called primes “the un-rectangleable numbers”, but it’s too late now. By the way, for most of human history, 1 was considered prime, but advances in our understanding of algebraic number theory eventually forced us to cull 1 from the primes. Sorry, 1.
5/ By the late 1700’s, it was quite fashionable to try to understand the distribution of the primes. The great German mathematician Carl Friedrich Gauss, then a teenager, computed massive tables of primes, which he used to experimentally scour for patterns.
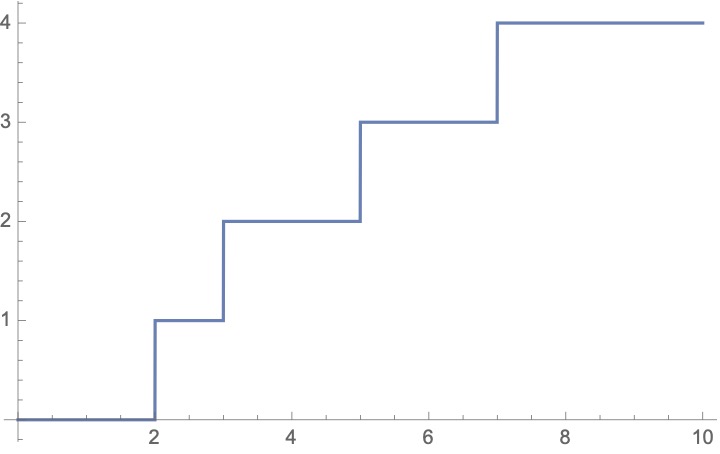
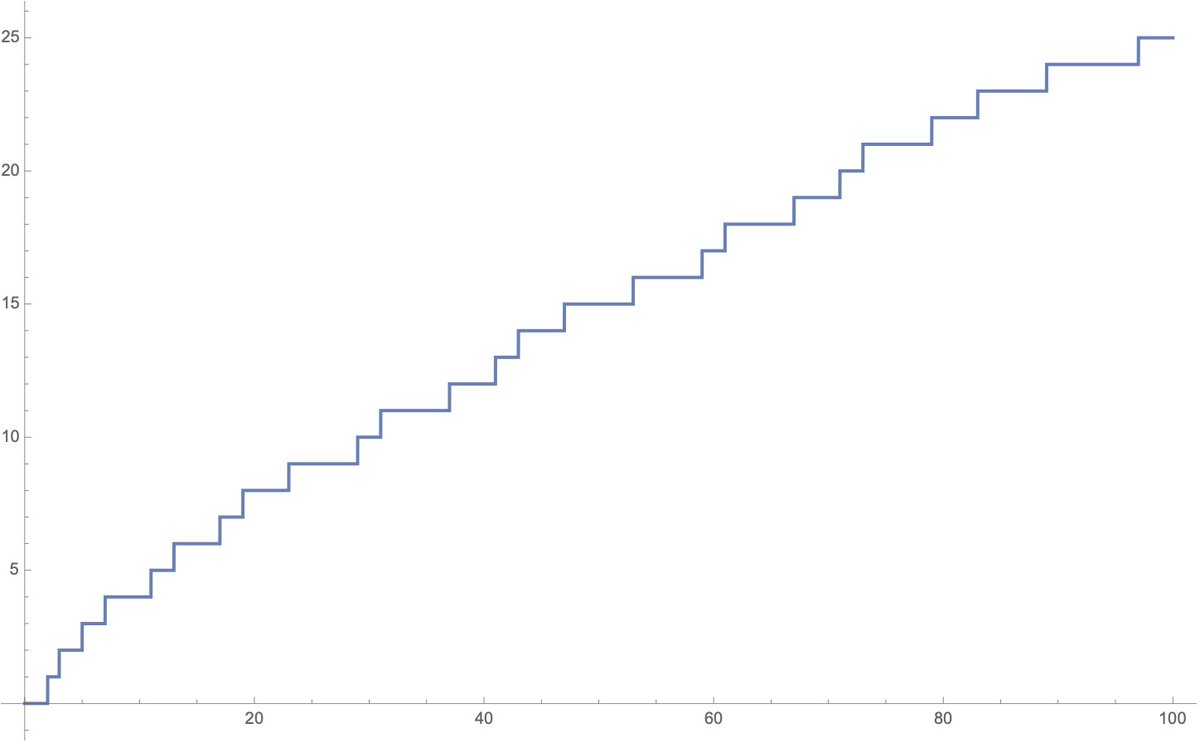
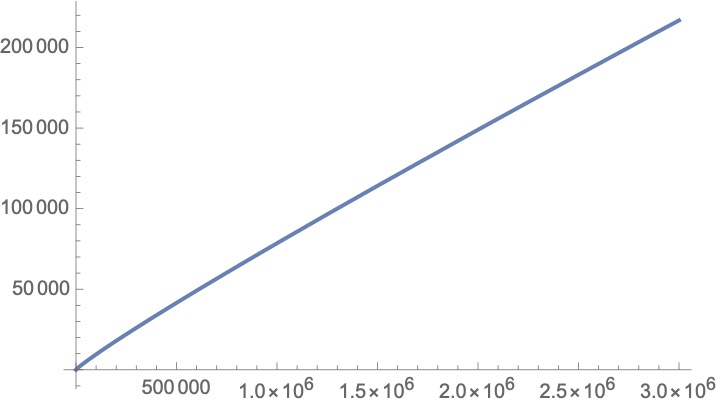
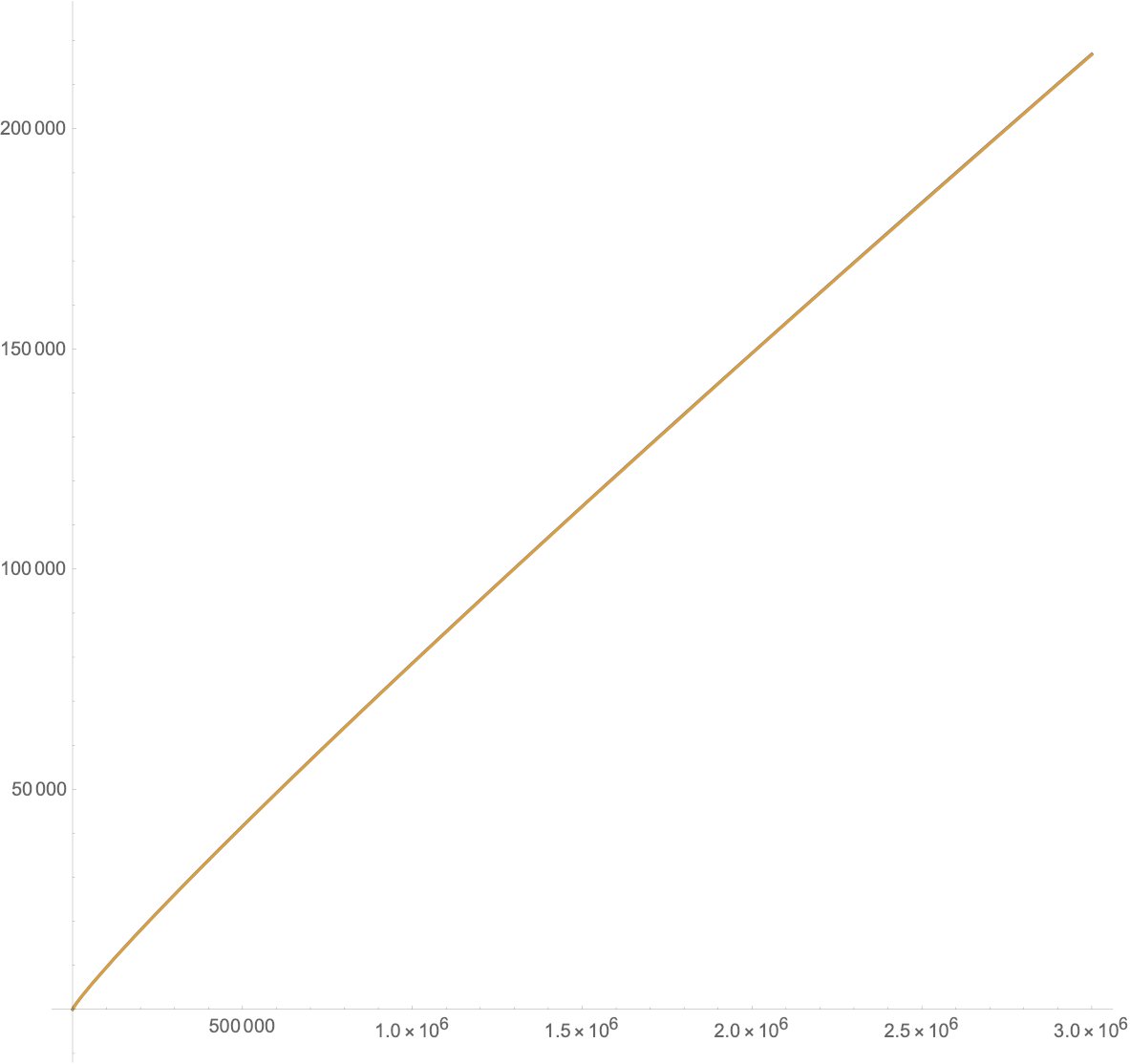
6/ We can plot the “Counting Function” of the primes, the graph of which stays flat until it hits a prime, at which point, it jumps up by one. Here’s the graph up to 10, and another up to 100. Do you see any patterns? Have a good, long stare. Here& #39;s another graph, now out to 3mil
7/ Miraculously, at this scale, all the bumps seem ironed out, leaving a smooth-looking curve. It seems like the slope of this curve is getting ever slightly flatter over time, almost as if it really does want to keep climbing, but gets more tired the higher up it goes.
8/ Put another way, large numbers are less and less “likely” to be prime; their proportion among their neighbors becomes smaller and smaller.
Luckily for us, Gauss was also fascinated with the (natural) logarithm function, log(x), and made lots of lots of tables and calculations
Luckily for us, Gauss was also fascinated with the (natural) logarithm function, log(x), and made lots of lots of tables and calculations
9/ leading him to the guess that the proportion of prime numbers decreases roughly at the rate 1/log x. One could say "the probability" of a number of size about x being prime is 1/log x (which is of course nonsense, it either is or isn& #39;t prime, but useful nonsense nonetheless).
10/ This suggests that the growth rate of the Prime Counting Function should be the same as that of:
F(x)=1/log 2 + 1/log 3 + ... +1/log x,
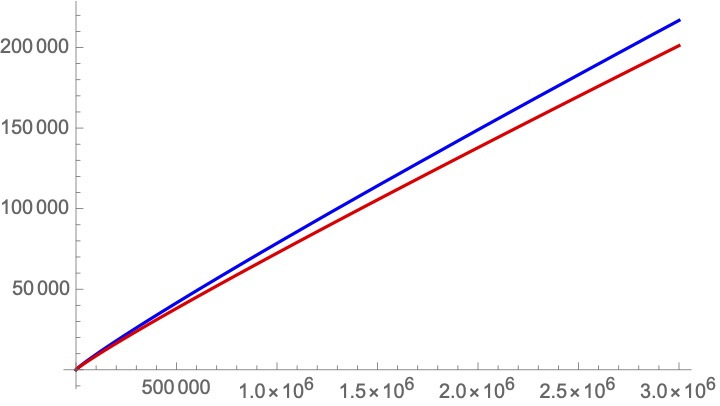
which is very close to the integral from 2 to x of 1/log t dt (called "Logarithmic Integral Function"). Here are the two side by side.
F(x)=1/log 2 + 1/log 3 + ... +1/log x,
which is very close to the integral from 2 to x of 1/log t dt (called "Logarithmic Integral Function"). Here are the two side by side.
11/ Do you see two curves or just one? They& #39;re right on top of each other, a near-perfect match!
By the way, many people say that the primes grow like x/log x. That& #39;s asymptotically correct, but waaay worse than F(x) itself -- see the two curves now?
By the way, many people say that the primes grow like x/log x. That& #39;s asymptotically correct, but waaay worse than F(x) itself -- see the two curves now?
12/ Just how well does F(x) approximate the Prime Counting Function? It takes my laptop 8 secs to compute the number of primes less than 3 quadrillion, the answer being
86,688,602,810,119
But F(x) is computed in 0.0002 seconds and gives the approximation:
86,688,604,682,699
86,688,602,810,119
But F(x) is computed in 0.0002 seconds and gives the approximation:
86,688,604,682,699
13/ Notice that these are 14 digit numbers, which agree to the first 7 digits -- *half* of the digits are accurate. THAT is the Riemann hypothesis! Namely, will the error always be about square-root of the approximation.
Let me make one last point before moving to Riemann& #39;s work
Let me make one last point before moving to Riemann& #39;s work
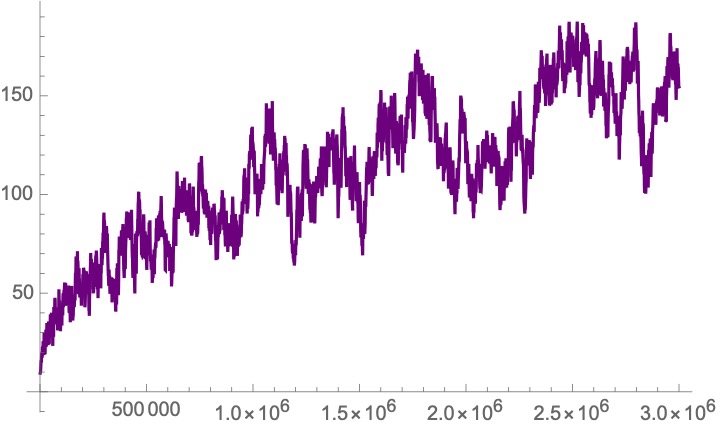
14/ Here is a plot of the difference between the Prime Counting Function (which is traditionally called Pi(x), but of course the public then gets very confused because Pi=3.14...) and Gauss& #39;s approximation F(x). Almost looks like a Brownian motion (again, that& #39;s RH! At time x,
15/ Brownian motion reaches distance about sqrt(x) from the origin). When looking at this curve, it is *very* tempting to conjecture that in fact the curve will always be positive. And it will be, for as far as we can calculate.
Because we can& #39;t calculate very far!!!
Because we can& #39;t calculate very far!!!
16/ Littlewood showed in 1914 that in fact these curves will cross infinitely often, and his student Skewes gave the first effective estimate of the value of x by which the curves *must* have crossed at least once ("Skewes number"). Today we know they cross by around 10^316.
17/ And that& #39;s exactly why we mathematicians insist on rigorous proof, not just preponderance of evidence from data! (Remember this for later!...)
Ok, on to Bernhard Riemann, who by 1859 holds the Gauss Chair of Mathematics at Gottingen. He returns to the Zeta function of Euler,
Ok, on to Bernhard Riemann, who by 1859 holds the Gauss Chair of Mathematics at Gottingen. He returns to the Zeta function of Euler,
18/ defined as:
zeta(s) = 1/1^s + 1/2^s + 1/3^s + 1/4^s +...
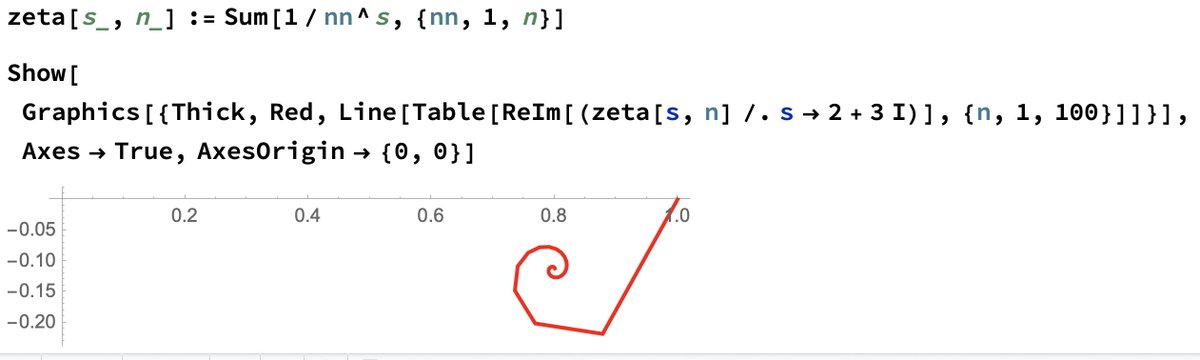
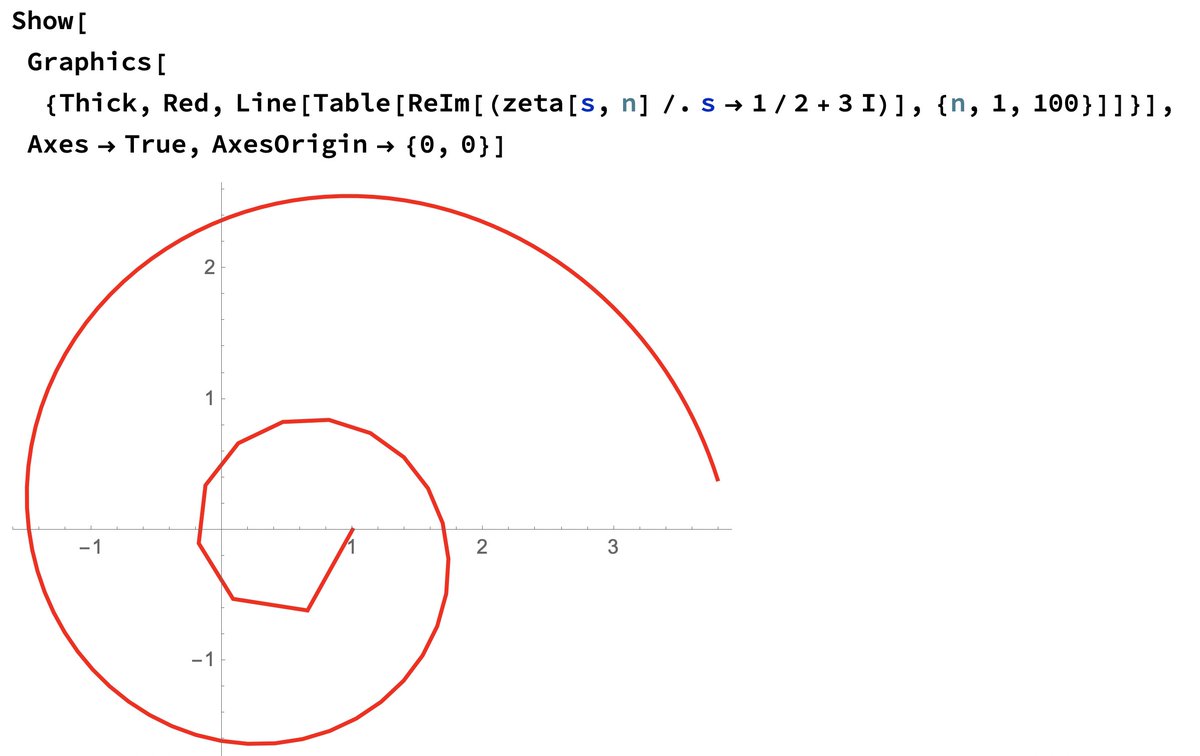
And allows s to be a complex number. For example, when s=2+3i, every time we add another term in the series, we get a new complex number. If we connect these, we see a fun "spiral" converging to the value of zeta:
zeta(s) = 1/1^s + 1/2^s + 1/3^s + 1/4^s +...
And allows s to be a complex number. For example, when s=2+3i, every time we add another term in the series, we get a new complex number. If we connect these, we see a fun "spiral" converging to the value of zeta:
19/ This works just fine if Re(s)>1 (since the series converges absolutely there), but already fails for s=1+3i, say. It just cycles around, not nearing a value. It& #39;s even worse for s=1/2+3i, where it spirals *out*!
Riemann found an amazing way to "renormalize" the spirals and
Riemann found an amazing way to "renormalize" the spirals and
20/ make sense of them despite the series converging. For the "proper" way to do this, see my complex analysis course. But a quicker version is to do this: notice that the integral of 1/t^s is t^(1-s)/(1-s). Turns out this is the "rate" at which the spirals blow up. Subtract this
21/ off and you get a nice, converging spiral again!
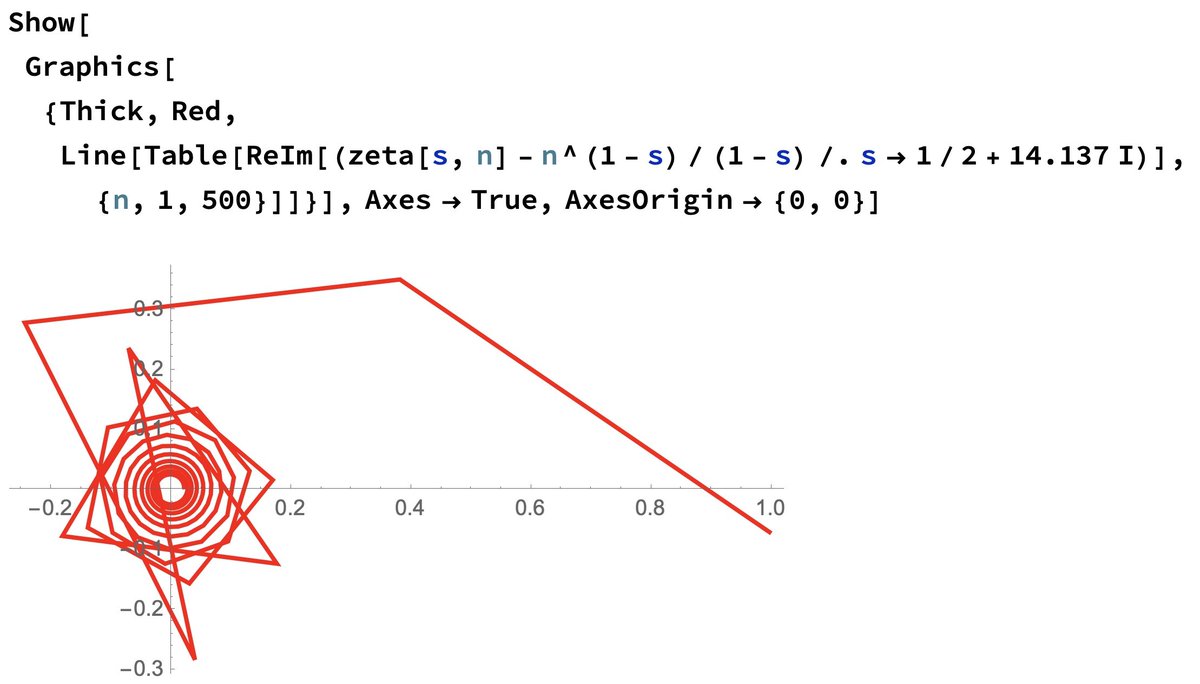
Now here& #39;s where the magic starts: For certain very special values of s, this spiral actually converges to Zero in the complex plane. The first time this happens is ...
Now here& #39;s where the magic starts: For certain very special values of s, this spiral actually converges to Zero in the complex plane. The first time this happens is ...
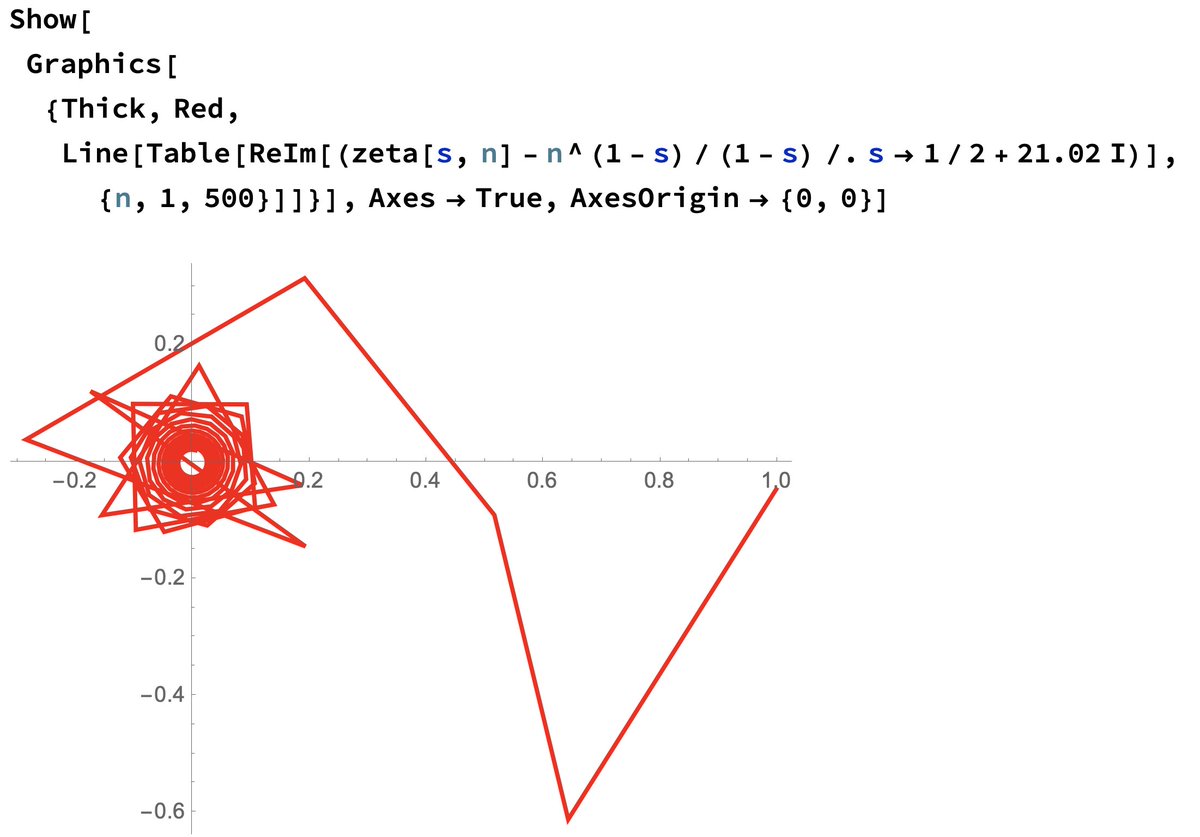
22/ when s=1/2+14.137i. See how it spirals, just like before, but now converging towards the origin? That& #39;s a zeta zero! It happens again when s=1/2+21.02i, and when s=1/2+25.01i, and so on. Riemann showed that for infinitely many s with real part between 0 and 1, zeta(s)=0.
23/ Riemann saw there was a symmetry in the values of zeta at s and at 1-s (and at the conjugate values), and "Hypothesized" that the zeros in this strip only occur on the central line, that is, when Re(s)=1/2 -- just like those few zeros we already saw.
24/ Finally, let& #39;s circle all the way back to the Prime Counting Function and see why these zeros determine the "missing harmonics" of the primes.
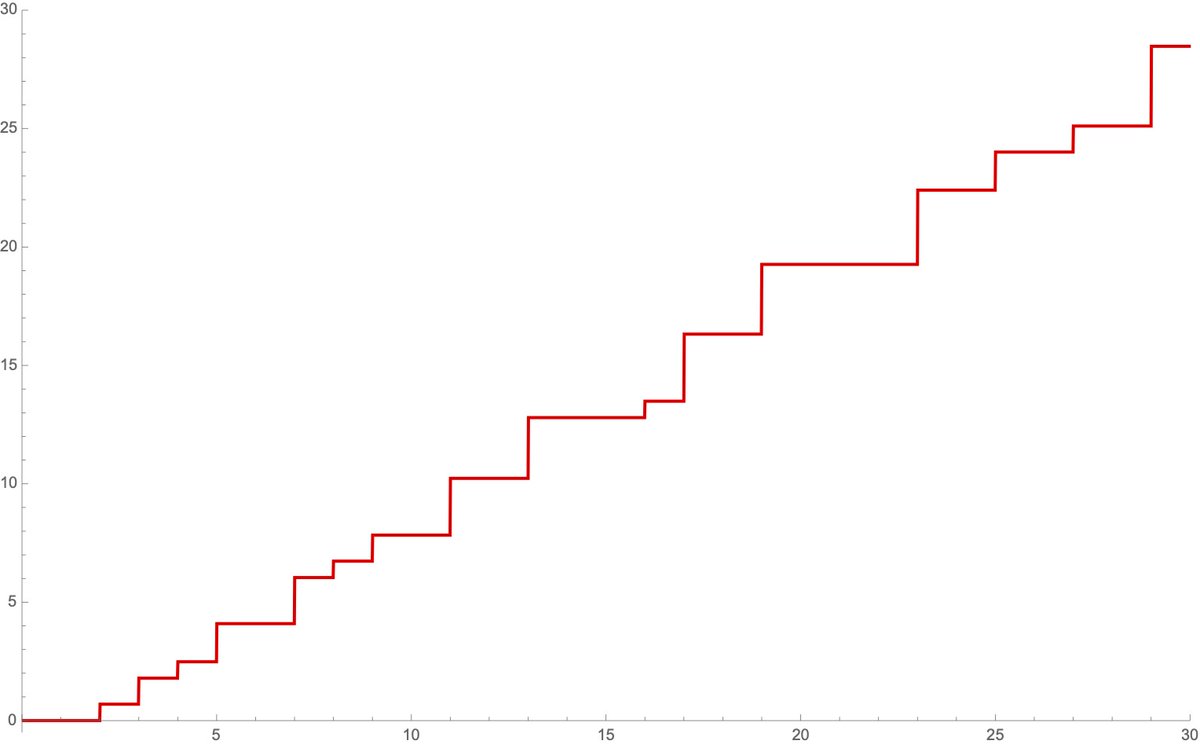
A slight change of variables makes things much cleaner. Let& #39;s change the counting function to increase not by 1 at every prime, but
A slight change of variables makes things much cleaner. Let& #39;s change the counting function to increase not by 1 at every prime, but
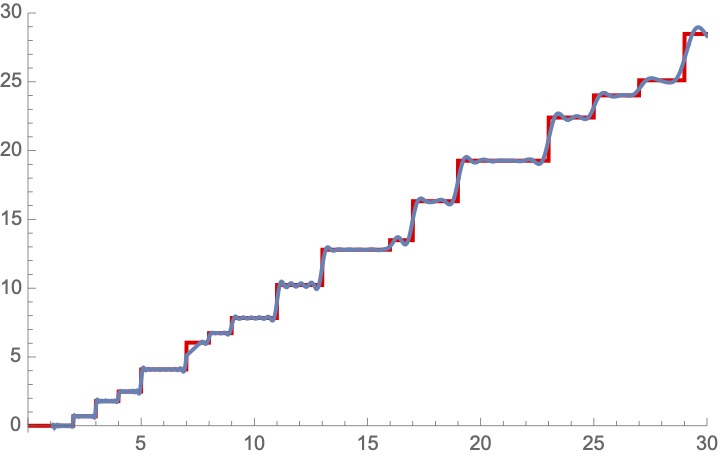
25/ by log p at the prime p, and also increase by log p at every power of p. Here& #39;s what this new function (sometimes called "Chebyshev& #39;s 2nd"...) looks like. (There& #39;s a very good reason for this function, which arises from the logarithmic derivative of zeta, but nevermind...)
26/ [I seem to have hit the Twitter thread limit, will have to continue in real time...]
We& #39;ve bumped the original prime counting function "up" by factors of log p, which exactly cancels out the "thinness" of the primes; this new counting function is now asymptotic to just y=x:
We& #39;ve bumped the original prime counting function "up" by factors of log p, which exactly cancels out the "thinness" of the primes; this new counting function is now asymptotic to just y=x:
27/ And here& #39;s where we finally see the analogy to music. For each zero of zeta, say rho, (so that zeta(rho)=0), we write down a "harmonic" function:
x^rho/rho + x^(1-rho)/(1-rho)
Looks complicated (remember the symmetry s->1-s), but actually it& #39;s just something like...
x^rho/rho + x^(1-rho)/(1-rho)
Looks complicated (remember the symmetry s->1-s), but actually it& #39;s just something like...
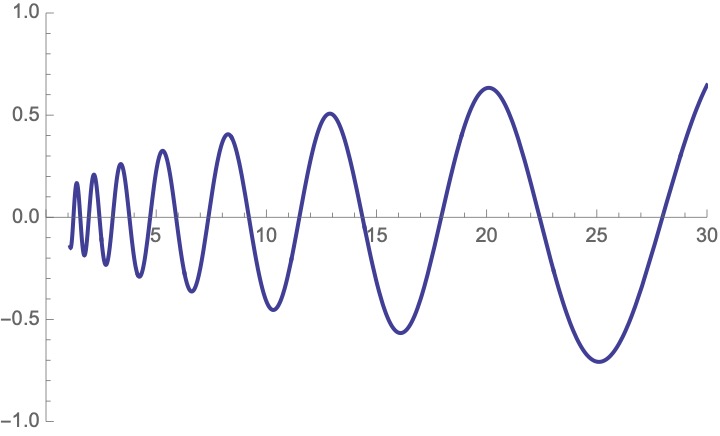
28/ sin(log x) with a growth factor of x^Re(rho). Here& #39;s the first one.
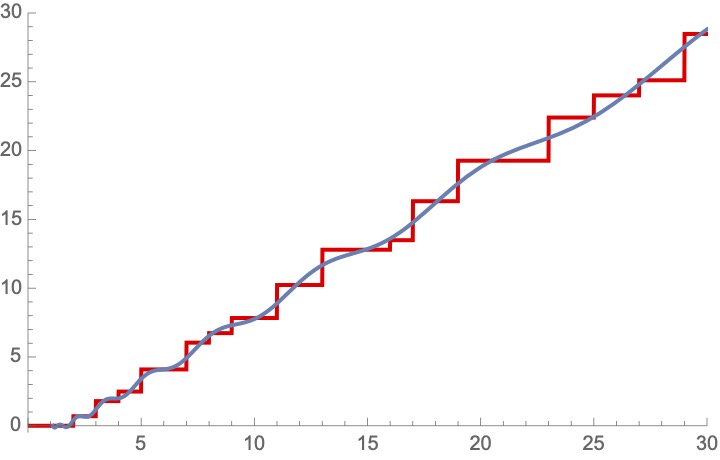
When we add this "wave" to the "harmonic" (y=x), we get their "superposition", which is the second pic.
When we add this "wave" to the "harmonic" (y=x), we get their "superposition", which is the second pic.
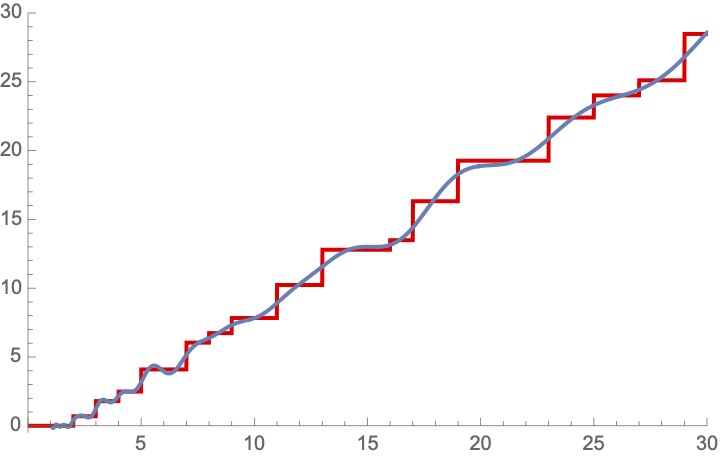
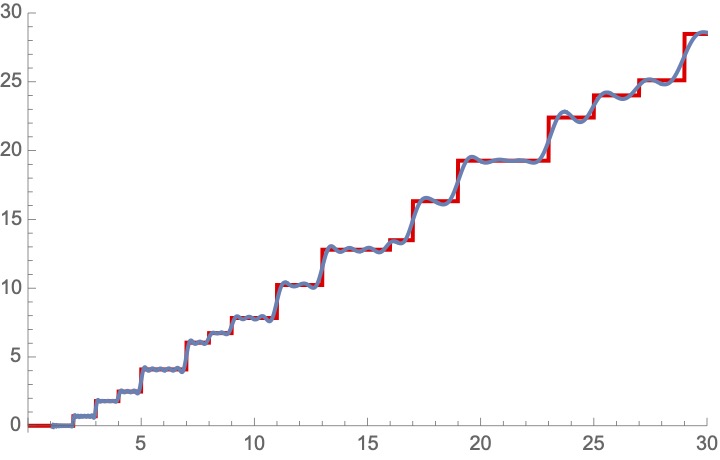
29/ Riemann rigorously proved that when you add up *all* of these harmonics using all the zeros of zeta, you exactly recover this modified prime counting function! These extra "waves" hear the "music" of the primes. Here are pics with 3, and 30, and 60 harmonics.
30/ Finally, here& #39;s the "meaning" of RH: Since all of these waves fluctuate at the rate x^Re(rho), and *if* all zeros rho have real part 1/2, then the fluctuations are all exactly at the same amplitude, sqrt x! *That& #39;s* why Li(x) predicts exactly half of the digits of Pi(x)! /end
PS: The point about Skewes number was to say: just because the first gazillion zeros have numerically been shown to be on the critical line is nowhere near enough evidence of it holding forever!...

 Read on Twitter
Read on Twitter






![26/ [I seem to have hit the Twitter thread limit, will have to continue in real time...]We& #39;ve bumped the original prime counting function "up" by factors of log p, which exactly cancels out the "thinness" of the primes; this new counting function is now asymptotic to just y=x: 26/ [I seem to have hit the Twitter thread limit, will have to continue in real time...]We& #39;ve bumped the original prime counting function "up" by factors of log p, which exactly cancels out the "thinness" of the primes; this new counting function is now asymptotic to just y=x:](https://pbs.twimg.com/media/E1IHPOBXMAMyahd.jpg)
![26/ [I seem to have hit the Twitter thread limit, will have to continue in real time...]We& #39;ve bumped the original prime counting function "up" by factors of log p, which exactly cancels out the "thinness" of the primes; this new counting function is now asymptotic to just y=x: 26/ [I seem to have hit the Twitter thread limit, will have to continue in real time...]We& #39;ve bumped the original prime counting function "up" by factors of log p, which exactly cancels out the "thinness" of the primes; this new counting function is now asymptotic to just y=x:](https://pbs.twimg.com/media/E1IHQOBXIAQZDa1.jpg)