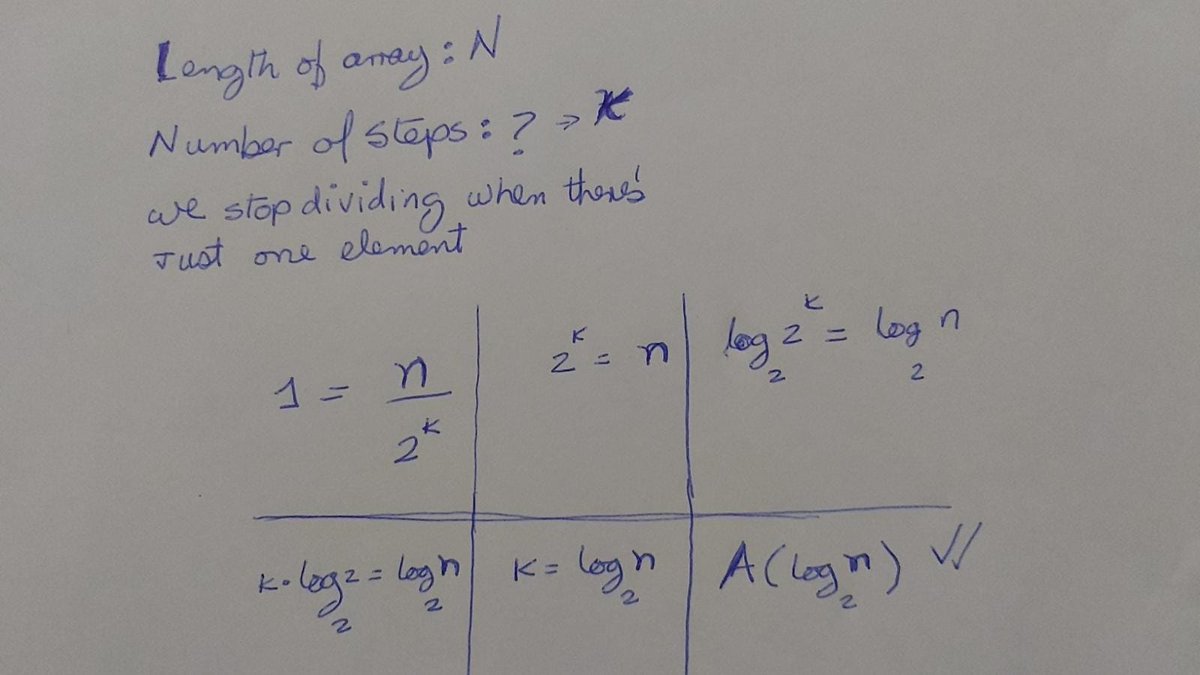Read on Twitter
These are my thoughts on Big O notation. I& #39;ll simplify as much as I can, but can& #39;t promise. Let& #39;s start with the general concept, then some Math and a couple of examples.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🧵" title="Thread" aria-label="Emoji: Thread">
1/n
1/n
A friend said: Big O is all about finding a mathematical function A that serves as upper bound to another function B (algorithm). That means independently from relationship between the amount of operations that B does & the time they take, A is "at some point" greater than B.
2/n
2/n
We can look at A like as follows: A(n) = y, where "n" is the more less the total amount of operations that B does, and "y" is *APPROXIMATELY* the units of time that this n operation take.
Why is it important to think in terms of operations ->"n" and not in terms of time?
3/n
Why is it important to think in terms of operations ->"n" and not in terms of time?
3/n
The thing is, measuring the efficiency of an algorithm just by looking at the amount of actual clock time that it takes to run isn& #39;t fair. That& #39;s because some architectures will easily outperform others given that CPUs have different rates of operation per second.
4/n
4/n
I find very useful before proceeding the concept of "family of functions". A family of functions is a concept that you can apply to group individual functions that have similar growing speed.
For instance, the following functions belong to the quadratic family or n^2.
5/n
For instance, the following functions belong to the quadratic family or n^2.
5/n
If we compare quadratic functions growth with cubic functions, the last one will start outperforming ALL the quadratic functions "at some point or for some value of x".
therefore 100*n^2 or 5n+8n^2 behave similarly as n^2 if compared with n^3
6/n
therefore 100*n^2 or 5n+8n^2 behave similarly as n^2 if compared with n^3
6/n
Keep in mind this:
n! > 2^n> n^k > n*log(n) > n > log(n) > k, with k being a positive integer
7/n
n! > 2^n> n^k > n*log(n) > n > log(n) > k, with k being a positive integer
7/n
To find our A function we agree that:
1) Variable creation or basic arithmetic operation cost 1 unit of time
2) A loop through all the elements of an array with N number of items cost N units of time.
3) Multiplication Principle: A loop with sth inside, cost N*t(Sth)
8/n
1) Variable creation or basic arithmetic operation cost 1 unit of time
2) A loop through all the elements of an array with N number of items cost N units of time.
3) Multiplication Principle: A loop with sth inside, cost N*t(Sth)
8/n
More rules to agree:
4) it& #39;s not always straight forward to figure out A
5) for recursive functions there& #39;s sth called the Master theorem that can help A LOT, link here:
9/n https://en.wikipedia.org/wiki/Master_theorem_(analysis_of_algorithms)">https://en.wikipedia.org/wiki/Mast...
4) it& #39;s not always straight forward to figure out A
5) for recursive functions there& #39;s sth called the Master theorem that can help A LOT, link here:
9/n https://en.wikipedia.org/wiki/Master_theorem_(analysis_of_algorithms)">https://en.wikipedia.org/wiki/Mast...
One thing more to keep in mind, we want our A function to be the lowest possible upper bound, which means that if B is performs constant operations (algorithm) then A shouldn& #39;t be cubic, quadratic or linear, A is also constant!
Okay, now we can solve a couple of examples
10/n
Okay, now we can solve a couple of examples
10/n
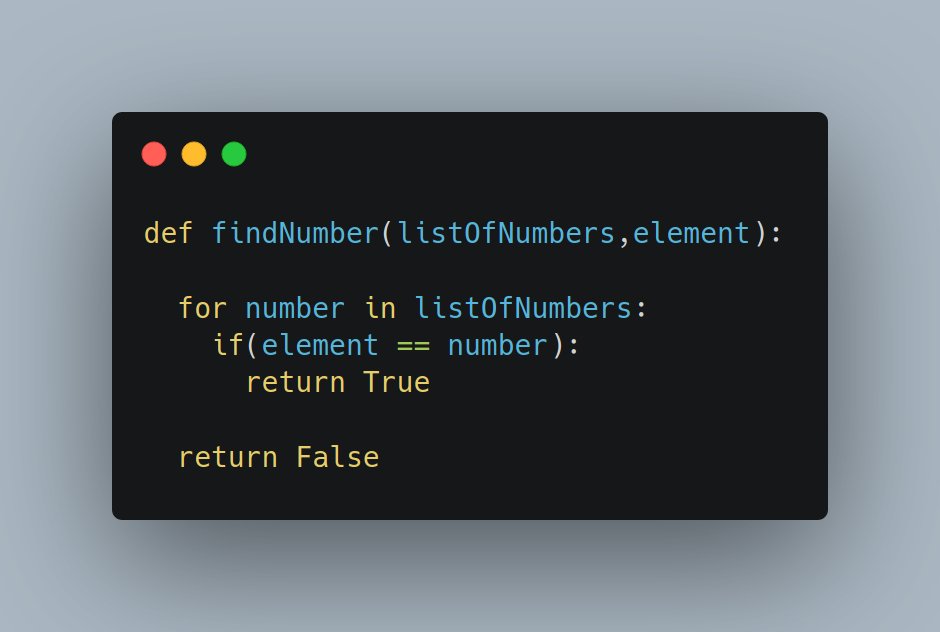
Ex1. Find a number in a list of numbers:
Best case will find the number in one step, but there& #39;s no guarantee that the element is present in the array, so worst case we should traverse the entire array. As we do N operations, our A function is the linear function t = n
11/n
Best case will find the number in one step, but there& #39;s no guarantee that the element is present in the array, so worst case we should traverse the entire array. As we do N operations, our A function is the linear function t = n
11/n
Ex2. Find a number in a sorted array. Let& #39;s apply Binary search, so instead of the code, I& #39;ll focus on finding A
The key here is that we are reducing the amount of operations in a half for each time that we repeat the loop.
so if B is Binary Search, then A is t=log(n)
12/n
The key here is that we are reducing the amount of operations in a half for each time that we repeat the loop.
so if B is Binary Search, then A is t=log(n)
12/n
Now let& #39;s ask a big question:
Why do we want to know all that?
The thing is, that once we have our upper bound A function, we can somehow tell how our B function will behave, cuz evaluating mathematical functions such a A is easier.
13/n
Why do we want to know all that?
The thing is, that once we have our upper bound A function, we can somehow tell how our B function will behave, cuz evaluating mathematical functions such a A is easier.
13/n
Interesting observations:
With all the above on mind we can analyze why are some problems NP, NP- hard or NP complete. In many of them the A function is exponential or non-polynomial but, to explain that, there& #39;s a fantastic thread to read.
https://twitter.com/AlejandroPiad/status/1390187493534822405?s=20
14/14">https://twitter.com/Alejandro...
With all the above on mind we can analyze why are some problems NP, NP- hard or NP complete. In many of them the A function is exponential or non-polynomial but, to explain that, there& #39;s a fantastic thread to read.
https://twitter.com/AlejandroPiad/status/1390187493534822405?s=20
14/14">https://twitter.com/Alejandro...
This is the more simplistically that I can go this time about Big O, hoping that it& #39;s not overwhelming as usual.
feel free to make any questions or corrections, I& #39;m open to hear your feedback.
Thanks @madeline_pc for somehow encourage me to write about this.
feel free to make any questions or corrections, I& #39;m open to hear your feedback.
Thanks @madeline_pc for somehow encourage me to write about this.
