Compounded returns experience "variance drain". This will be true if your bet size or allocation is a fixed percent of your wealth, savings, bankroll etc
Was messing with some coin flip stuff and got diverted by an illustration of geometric returns I figured I& #39;d post...
Was messing with some coin flip stuff and got diverted by an illustration of geometric returns I figured I& #39;d post...
First some quick intuition.
If you bet 1% of your wealth on a coin flip and win then lose, you are net down money. This is symmetrical. If you lose, then win, still down money.
1.01 * .99 = .99 * 1.01
This is compounding land
If you bet 1% of your wealth on a coin flip and win then lose, you are net down money. This is symmetrical. If you lose, then win, still down money.
1.01 * .99 = .99 * 1.01
This is compounding land
In additive or non-compounding land we bet a fixed dollar amount regardless of wealth.
So if I start with $100 and win a flip, then bet $1 again and lose the flip I& #39;m back to $100.
The $1 I bet when my bankroll was less than 1% of my bankroll.
Additive world is not % world
So if I start with $100 and win a flip, then bet $1 again and lose the flip I& #39;m back to $100.
The $1 I bet when my bankroll was less than 1% of my bankroll.
Additive world is not % world
The order of win then lose, or lose then win leaves you in the same place in both worlds.
The order does not matter if we are consistent about how we size the bet so long as we are consistent to the style whether it& #39;s fixed dollar or fixed percentage.
Let& #39;s continue
The order does not matter if we are consistent about how we size the bet so long as we are consistent to the style whether it& #39;s fixed dollar or fixed percentage.
Let& #39;s continue
The difference in the above examples is in compound world (ie fixed percentage) you are down and additive world (fixed dollar) you are unched.
So is fixed percentage somehow "bad" in that it opens you up to volatility or variance "drag"?
So is fixed percentage somehow "bad" in that it opens you up to volatility or variance "drag"?
Let& #39;s look at the case where instead of alternating wins and losses we trend. Win-win or lose-lose.
In the additive case we are either up 2% or down 2% on our initial bankroll.
Compounded case is up 2.01% or down 1.99%.
Better off both ways!
In the additive case we are either up 2% or down 2% on our initial bankroll.
Compounded case is up 2.01% or down 1.99%.
Better off both ways!
So the compounded case is better when we trend and worse when we "chop".
If bet a fixed percent of our bankroll fair coin toss game we are in compound return land.
It& #39;s a fair game. So our expectancy is zero. That& #39;s true even in compound land. But there& #39;s more to consider.
If bet a fixed percent of our bankroll fair coin toss game we are in compound return land.
It& #39;s a fair game. So our expectancy is zero. That& #39;s true even in compound land. But there& #39;s more to consider.
Compounding alters the distribution of our terminal wealth even if the expected outcome is unchanged.
The median outcome is actually negative. In other words, your net p/l is negative more often than it& #39;s positive.
Why?
It goes back to the trend vs the chop.
The median outcome is actually negative. In other words, your net p/l is negative more often than it& #39;s positive.
Why?
It goes back to the trend vs the chop.
The median is negative but the mean is zero.
Compounding likes trending and hates chopping as we saw earlier.
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="🪓" title="Axt" aria-label="Emoji: Axt"> Chopping happens more 𝐨𝐟𝐭𝐞𝐧 so you get a negative median
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🪓" title="Axt" aria-label="Emoji: Axt"> Chopping happens more 𝐨𝐟𝐭𝐞𝐧 so you get a negative median
...but this is balanced by a larger trending bonus due to compounding.
Let& #39;s illustrate
Compounding likes trending and hates chopping as we saw earlier.
...but this is balanced by a larger trending bonus due to compounding.
Let& #39;s illustrate
First let& #39;s quickly allude back to additive vs compounding.
Let& #39;s see how I denote the "compounding bonus/drag"
Let& #39;s see how I denote the "compounding bonus/drag"
There& #39;s 4 actual scenarios:
2u (trend)
1u, 1d (chop)
1d, 1u (chop)
2d (trend)
Things to note:
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">Chop and trend happen equally.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">Chop and trend happen equally.
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The magnitude of the boost/drag is also equal.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The magnitude of the boost/drag is also equal.
2u (trend)
1u, 1d (chop)
1d, 1u (chop)
2d (trend)
Things to note:
How about 3 flips?
There& #39;s 8 total outcomes, but again order doesn& #39;t matter. So there& #39;s really just 4 outcomes.
The "chops" are bolded. They represent compounding "drag"
Note:
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> You drag 75% of the time!
https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> You drag 75% of the time!
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> The larger positive boost magnitudes make up for the frequency.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> The larger positive boost magnitudes make up for the frequency.
There& #39;s 8 total outcomes, but again order doesn& #39;t matter. So there& #39;s really just 4 outcomes.
The "chops" are bolded. They represent compounding "drag"
Note:
Now that you have the gist, let& #39;s do 10 flips.
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">65% of the results are chop giving you compounding drag
https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">65% of the results are chop giving you compounding drag
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The times you trend though crush your performance if you only bet fixed dollar!
https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The times you trend though crush your performance if you only bet fixed dollar!
Let& #39;s take a look visually at the paths to see the "chop".
Pascal& #39;s https://abs.twimg.com/emoji/v2/... draggable="false" alt="🔺" title="Nach oben zeigendes rotes Dreieck" aria-label="Emoji: Nach oben zeigendes rotes Dreieck">is a quick way to to get the coefficients of a binomial tree. The coefficients represent combinations which are weighted by the probabilities in the binomial expansion.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🔺" title="Nach oben zeigendes rotes Dreieck" aria-label="Emoji: Nach oben zeigendes rotes Dreieck">is a quick way to to get the coefficients of a binomial tree. The coefficients represent combinations which are weighted by the probabilities in the binomial expansion.
I enclosed the "chop" or drag paths
Pascal& #39;s
I enclosed the "chop" or drag paths
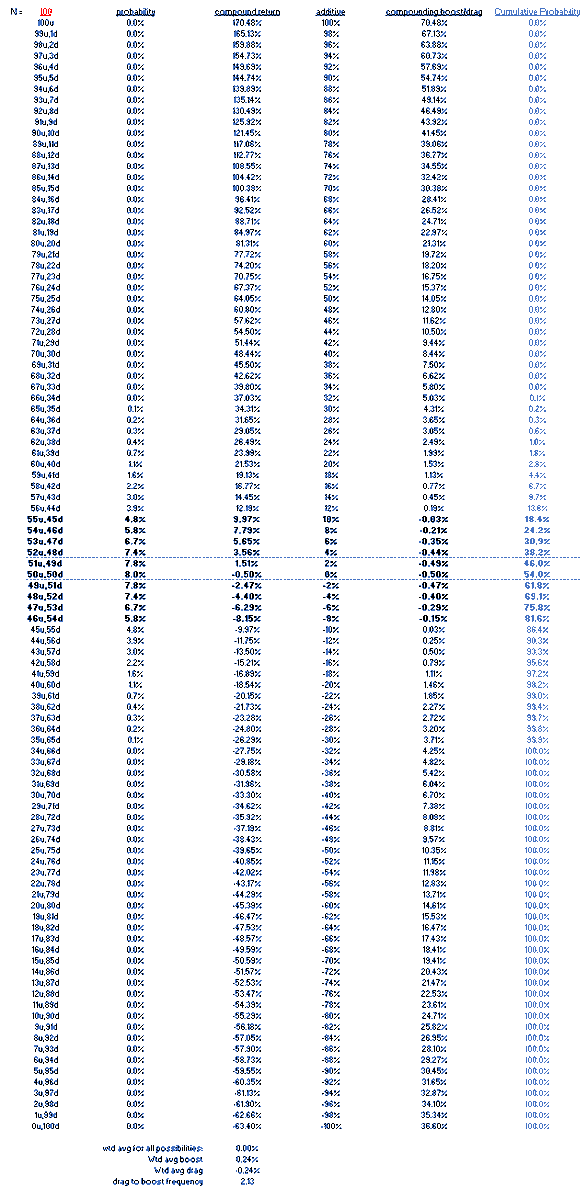
Let& #39;s do this with 100 flips where the negative median now becomes very apparent in the "cumulative probability" column.
The chop occurs in 68% of paths. The median return is -.50% after 100 flips though the expectancy is still zero.
The chop occurs in 68% of paths. The median return is -.50% after 100 flips though the expectancy is still zero.
In additive world if you win 50 $1 bets and lose 50 $1 bets your p/l is zero.
In compounding world, where you bet 1% each time you are down 50 bps in that scenario.
Your overall expectancy is zero because the common chop balances the rare but heavily compounding trends.
In compounding world, where you bet 1% each time you are down 50 bps in that scenario.
Your overall expectancy is zero because the common chop balances the rare but heavily compounding trends.
Paths affect distribution of p/l even if they don& #39;t affect expectancy.
Since we actually experience "path" and all its attendant emotions, it pays to think about the composition of expectancy and returns.
Stay groovy
(Older post if you want more: https://moontowermeta.com/the-volatility-drain/)">https://moontowermeta.com/the-volat...
Since we actually experience "path" and all its attendant emotions, it pays to think about the composition of expectancy and returns.
Stay groovy
(Older post if you want more: https://moontowermeta.com/the-volatility-drain/)">https://moontowermeta.com/the-volat...

 Read on Twitter
Read on Twitter
 Chop and trend happen equally. https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The magnitude of the boost/drag is also equal." title="There& #39;s 4 actual scenarios:2u (trend)1u, 1d (chop)1d, 1u (chop) 2d (trend)Things to note:https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">Chop and trend happen equally. https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The magnitude of the boost/drag is also equal." class="img-responsive" style="max-width:100%;"/>
Chop and trend happen equally. https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The magnitude of the boost/drag is also equal." title="There& #39;s 4 actual scenarios:2u (trend)1u, 1d (chop)1d, 1u (chop) 2d (trend)Things to note:https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">Chop and trend happen equally. https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The magnitude of the boost/drag is also equal." class="img-responsive" style="max-width:100%;"/>
 You drag 75% of the time!https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> The larger positive boost magnitudes make up for the frequency." title="How about 3 flips?There& #39;s 8 total outcomes, but again order doesn& #39;t matter. So there& #39;s really just 4 outcomes. The "chops" are bolded. They represent compounding "drag"Note:https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> You drag 75% of the time!https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> The larger positive boost magnitudes make up for the frequency." class="img-responsive" style="max-width:100%;"/>
You drag 75% of the time!https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> The larger positive boost magnitudes make up for the frequency." title="How about 3 flips?There& #39;s 8 total outcomes, but again order doesn& #39;t matter. So there& #39;s really just 4 outcomes. The "chops" are bolded. They represent compounding "drag"Note:https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> You drag 75% of the time!https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen"> The larger positive boost magnitudes make up for the frequency." class="img-responsive" style="max-width:100%;"/>
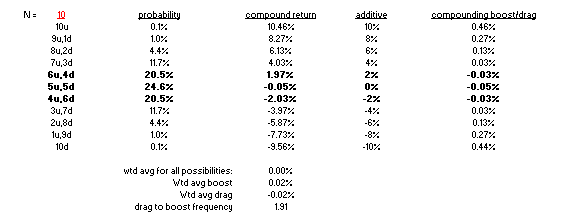 65% of the results are chop giving you compounding draghttps://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The times you trend though crush your performance if you only bet fixed dollar!" title="Now that you have the gist, let& #39;s do 10 flips.https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">65% of the results are chop giving you compounding draghttps://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The times you trend though crush your performance if you only bet fixed dollar!" class="img-responsive" style="max-width:100%;"/>
65% of the results are chop giving you compounding draghttps://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The times you trend though crush your performance if you only bet fixed dollar!" title="Now that you have the gist, let& #39;s do 10 flips.https://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">65% of the results are chop giving you compounding draghttps://abs.twimg.com/emoji/v2/... draggable="false" alt="✔️" title="Fettes Häkchen" aria-label="Emoji: Fettes Häkchen">The times you trend though crush your performance if you only bet fixed dollar!" class="img-responsive" style="max-width:100%;"/>
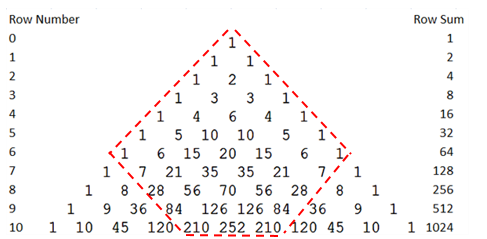 is a quick way to to get the coefficients of a binomial tree. The coefficients represent combinations which are weighted by the probabilities in the binomial expansion. I enclosed the "chop" or drag paths" title="Let& #39;s take a look visually at the paths to see the "chop". Pascal& #39;shttps://abs.twimg.com/emoji/v2/... draggable="false" alt="🔺" title="Nach oben zeigendes rotes Dreieck" aria-label="Emoji: Nach oben zeigendes rotes Dreieck">is a quick way to to get the coefficients of a binomial tree. The coefficients represent combinations which are weighted by the probabilities in the binomial expansion. I enclosed the "chop" or drag paths" class="img-responsive" style="max-width:100%;"/>
is a quick way to to get the coefficients of a binomial tree. The coefficients represent combinations which are weighted by the probabilities in the binomial expansion. I enclosed the "chop" or drag paths" title="Let& #39;s take a look visually at the paths to see the "chop". Pascal& #39;shttps://abs.twimg.com/emoji/v2/... draggable="false" alt="🔺" title="Nach oben zeigendes rotes Dreieck" aria-label="Emoji: Nach oben zeigendes rotes Dreieck">is a quick way to to get the coefficients of a binomial tree. The coefficients represent combinations which are weighted by the probabilities in the binomial expansion. I enclosed the "chop" or drag paths" class="img-responsive" style="max-width:100%;"/>