Triple product L-functions arise naturally in (at least) the following two ways:

1) (Arithmetic) Quantum Unique Ergodicity (AQUE)
2) Langlands functoriality for GL(2)xGL(2)

Let's first talk about AQUE (for which Lindenstrauss won a Fields). The simplest setting is: ... https://twitter.com/anton_hilado/status/1314761390947786755

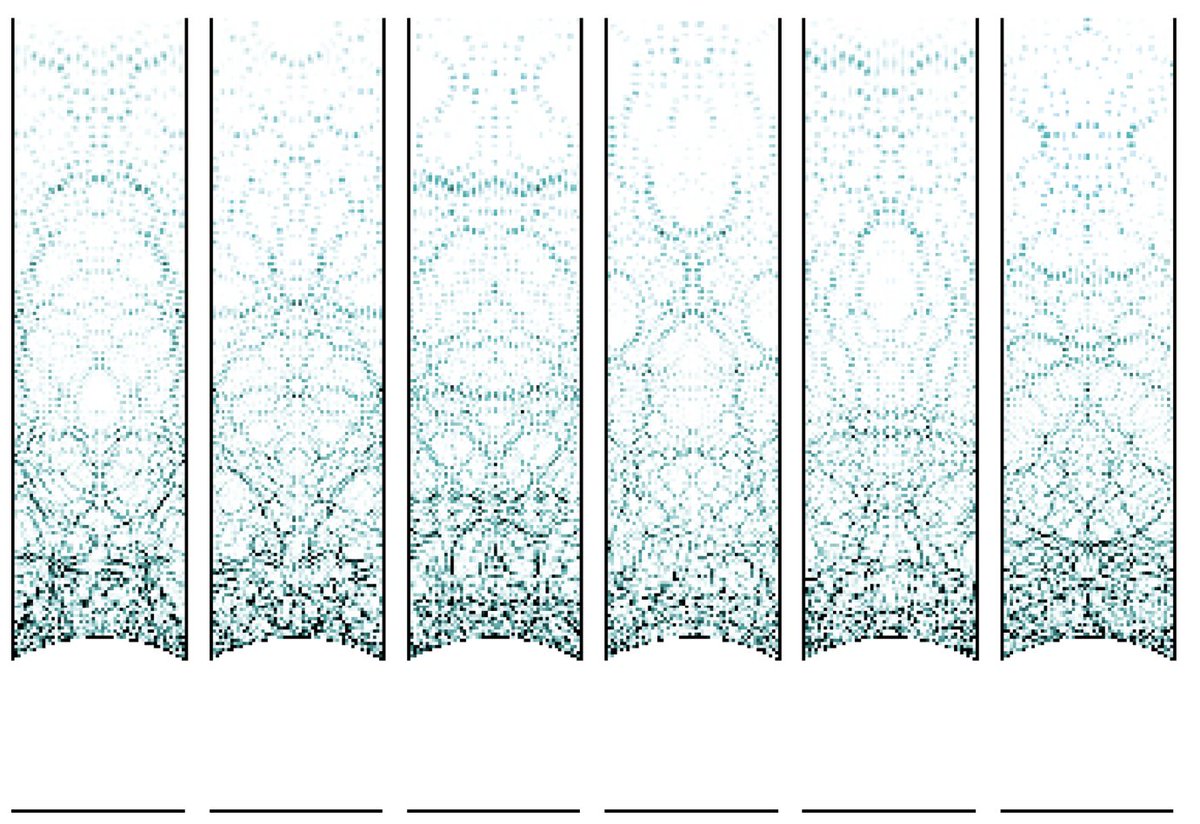
2/ you have a surface M and look at the Laplacian acting on L^2(M) (really the unit tangent bundle of M, where geodesic flow lives, but nevermind...). Each eigenfunction phi gives rise to a probability measure |phi|^2 dx, and a basic question in quantum chaos is: what happens ...

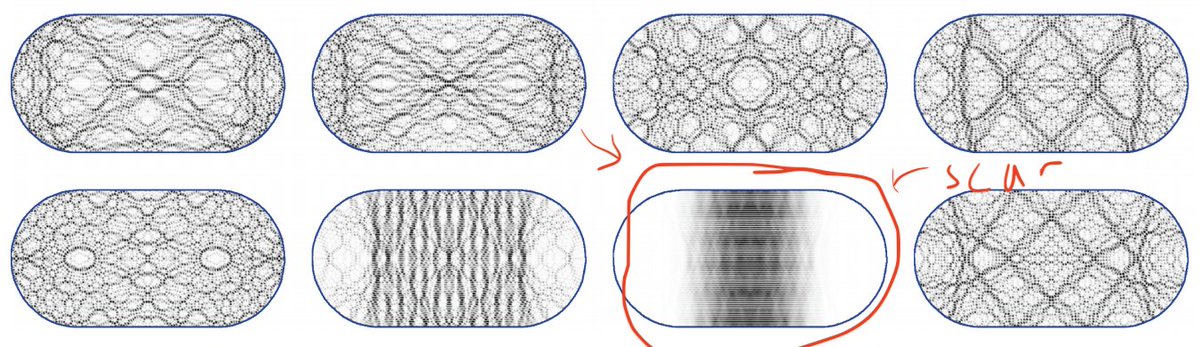
3/ to these measures in the high energy limit, meaning as the eigenvalue increases. Shnirelman showed in the 70's that for *most* such sequences, the measures converge to uniform ("quantum ergodicity"). Sinai's student Bunimovich studied the "stadium", and showed that there was..

4/ "scarring", that is, there were (sparse) subsequences of eigenfunctions along which these measures remained non-uniform. In the 90s, Rudnick and Sarnak proposed a bold conjecture: if M has negative curvature, then the *only* limit along any subsequence is uniform measure.

5/ This is quantum *unique* ergodicity (in the quantum limit, there is a unique ergodic measure, and hence a unique geodesic flow - invariant measure).

This remains *completely unproved*, even for a single example of M. But! If M=SL(2,Z)\\H, say, then one has extra symmetries ...

6/ coming from the Hecke operators, which one can exploit! If phi is such an eigenfunction (Maass form), *and* is an eigenfunction of all Hecke operators (which is expected to be automatic; the eigenvalues should have multiplicity one - unproved!), then to study the measure...

7/ |phi|^2 dx, one can evaluate it on a "test vector" f, which one can also assume is a Laplace and Hecke eigenfunction. So one needs to integrate \\int_M f |phi|^2, and show that this decays as the eigenvalue lambda_phi -> infty. In 2001, Sarnak's student Watson proved an amazing

8/ formula: for 3 such eigenfunctions, f, g, h:

\\int_M f g h ~ L(f x g x h,1/2),

that is, up to well-understood things, the integral is the central value of a triple-product L-function of GL(2)xGL(2)xGL(2) (hypothetically on GL(8))! Here's a simple way to think about these:

9/ If L(f,s) = prod_p L_p(f,s), then the local factors look like:

L_p(f,s)=(1-a1/p^s)^-1 (1- a2 / p^s)^-1.

Here a1,a2 are the "Langlands-Satake parameters". If g has parameters b1,b2, and h has c1,c2, then

L_p(fxgxh,s)=prod(1-abc/p^s)^-1,

where the product is over a=a1, a2,

10/ b=b1 or b2, and c=c1 or c2. (So there are 2^3=8 terms in the product, and this is a degree 8 L-function, expected by Langlands to be the L-function of some automorphic representation on GL(8).)

Anyway, back to QUE, one would need to prove a "subconvex estimate" for the ...

11/ resulting central L-value to conclude AQUE. This is expected from Lindelof (consequence of GRH), but still has not been done! (Except for log savings by Sound and Holowinsky in the holomorphic QUE, but nevermind...) Lindenstrauss bypassed this issue by looking at S-arithmetic

12/ versions and using Hecke operators more directly (in analogy with Furstenberg x2x3...).

Anyway, I've gone on too long now, so let me mumble something quickly for functoriality. The Cogdell-Piatetski-Shapiro converse theorem says that: if you have a degree n L-function,

13/ and you know that all twisted Rankin-Selberg L-functions by GL(n-2) have functional equations (and some other stuff...), then your L-function comes from a GL(n) form. So if you're trying to prove functoriality of GL(2)xGL(2), which should be on GL(4), guess what you need to

14/ twist it by? Yep, GL(2), meaning you need functional equations of L(s,GL(2)xGL(2)xGL(2)) -- the triple product L-function again! An integral representation was constructed by Garrett, and then used by Ramakrishnan to prove functoriality.

Hope that helps somewhat...?