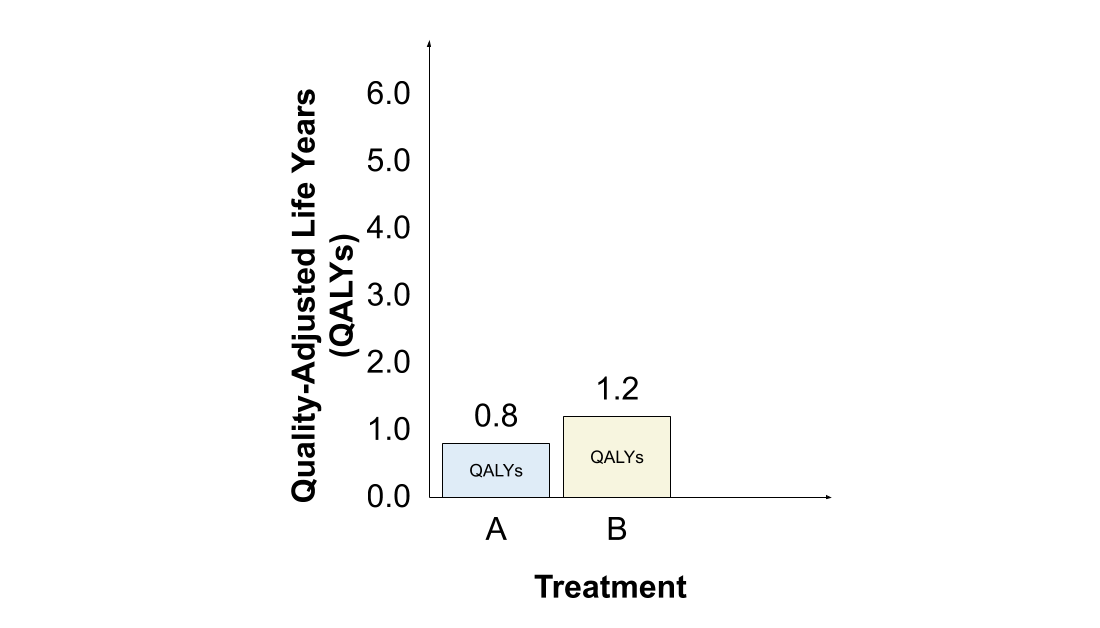In response to my presentation at #SMDM20, @TMSnowsill has raised the issue of
treatments which extend life but provide zero health-related quality-of-life (HRQoL). How do the #QALY, #LY, #evLYG and #HYT deal with these? [Thread] @icer_review @Basucally https://www.youtube.com/watch?v=MtNKI2VfTJw&feature=youtu.be">https://www.youtube.com/watch... https://www.youtube.com/watch...
treatments which extend life but provide zero health-related quality-of-life (HRQoL). How do the #QALY, #LY, #evLYG and #HYT deal with these? [Thread] @icer_review @Basucally https://www.youtube.com/watch?v=MtNKI2VfTJw&feature=youtu.be">https://www.youtube.com/watch... https://www.youtube.com/watch...
In this thread I will also consider how each of these four approaches deals with treatments that extend a patient& #39;s life but with a *negative* HRQoL (i.e. in a state & #39;worse than dead& #39;), and offer some thoughts on the implications of this for decision making.
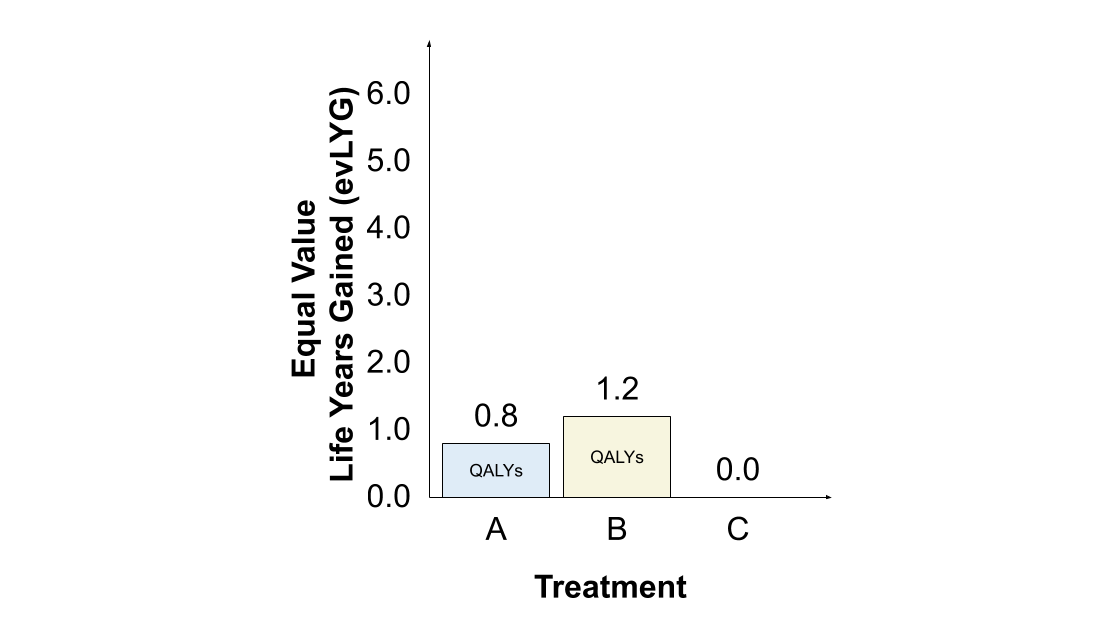
As an illustrative example, suppose we initially have just two treatments, A and B. Treatment A provides good HRQoL (0.8) for 1 year, while treatment B provides slightly worse HRQoL (0.6) for 2 years. Let& #39;s begin by considering how each approach values treatments A and B.
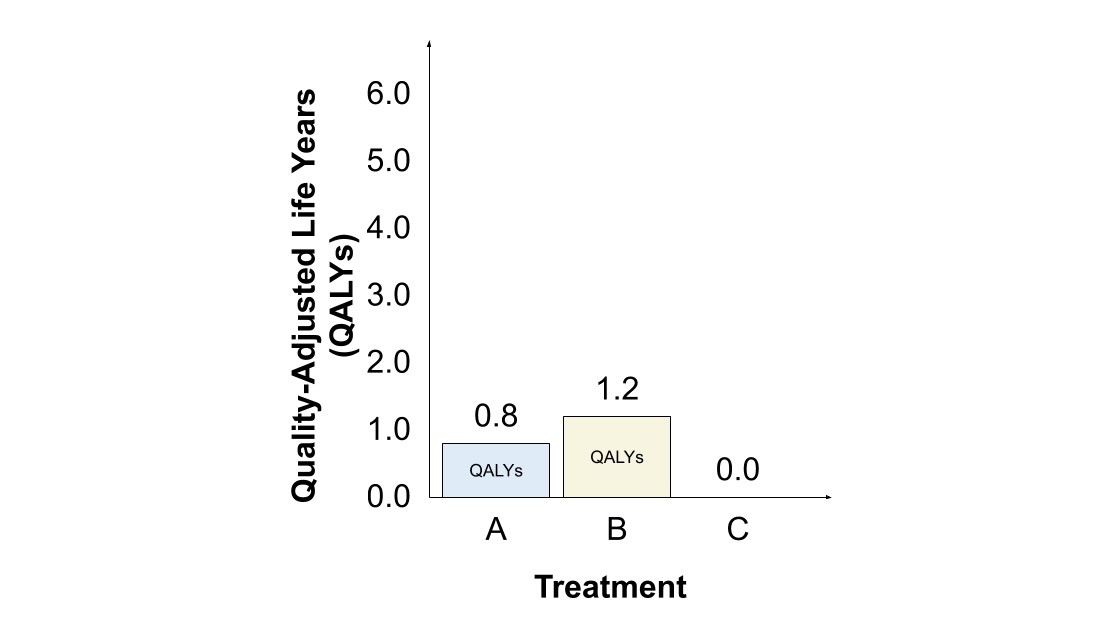
The #QALY assigns greater value to treatment B than to treatment A, since 2 years valued at 0.6 each (1.2 QALYs) is greater than 1 year valued at 0.8 (0.8 QALYs).
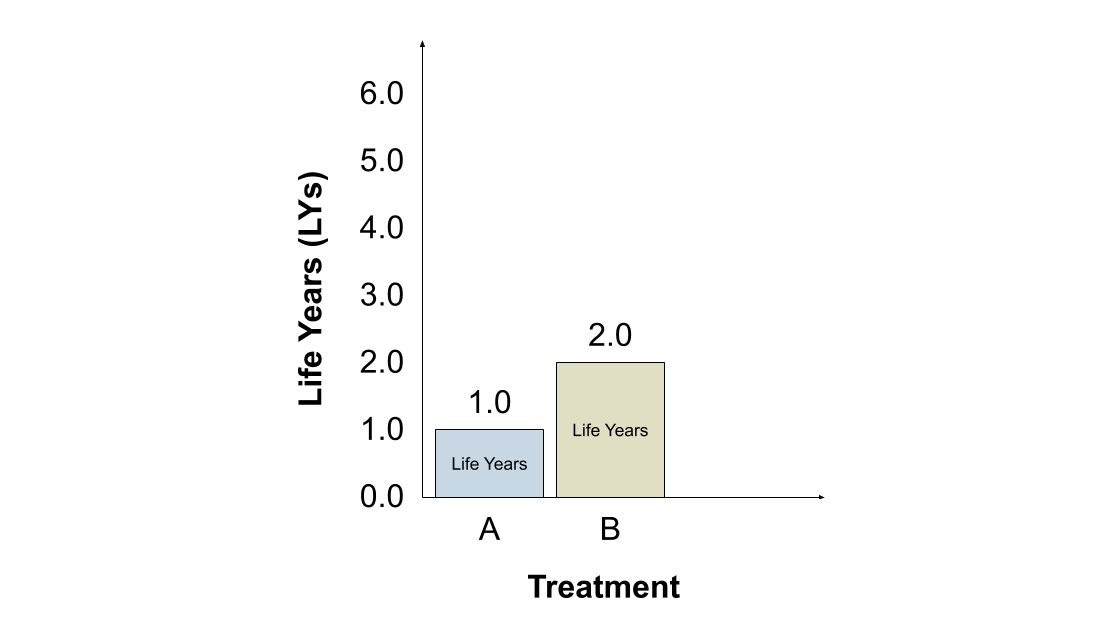
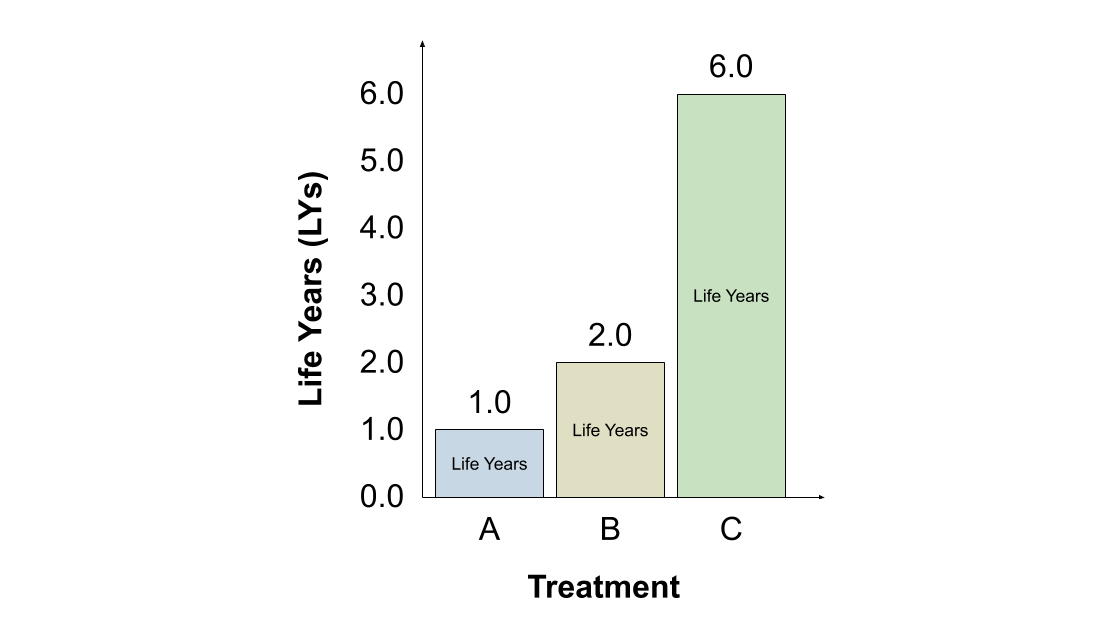
The #LY approach also assigns greater value to treatment B, since it offers longer life expectancy (2 years) than treatment A (1 year). Note that HRQoL is irrelevant under the #LY approach.
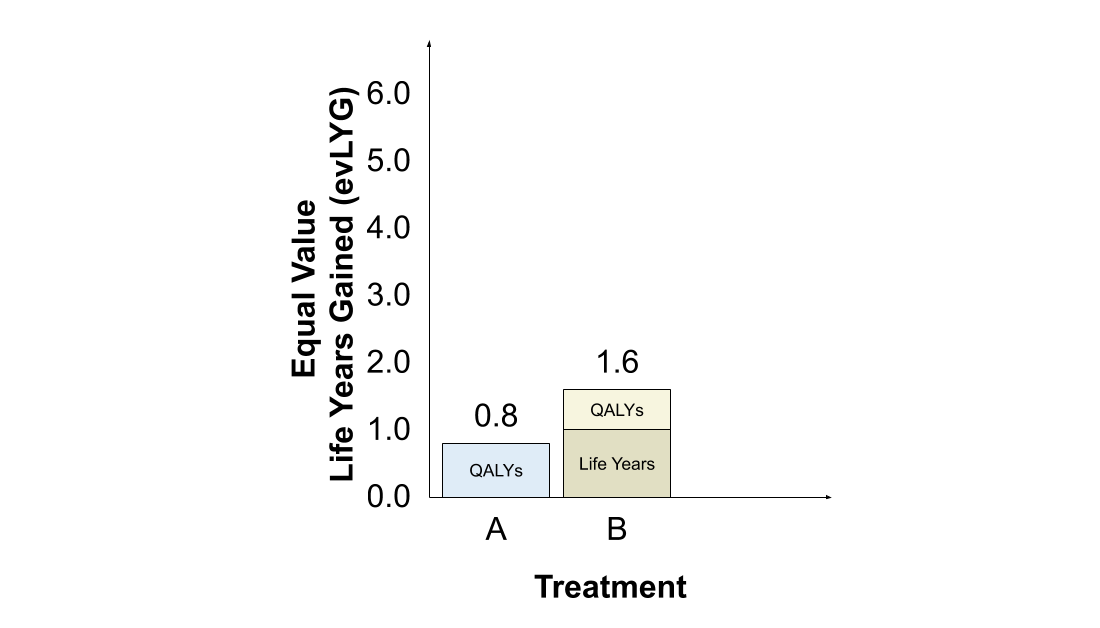
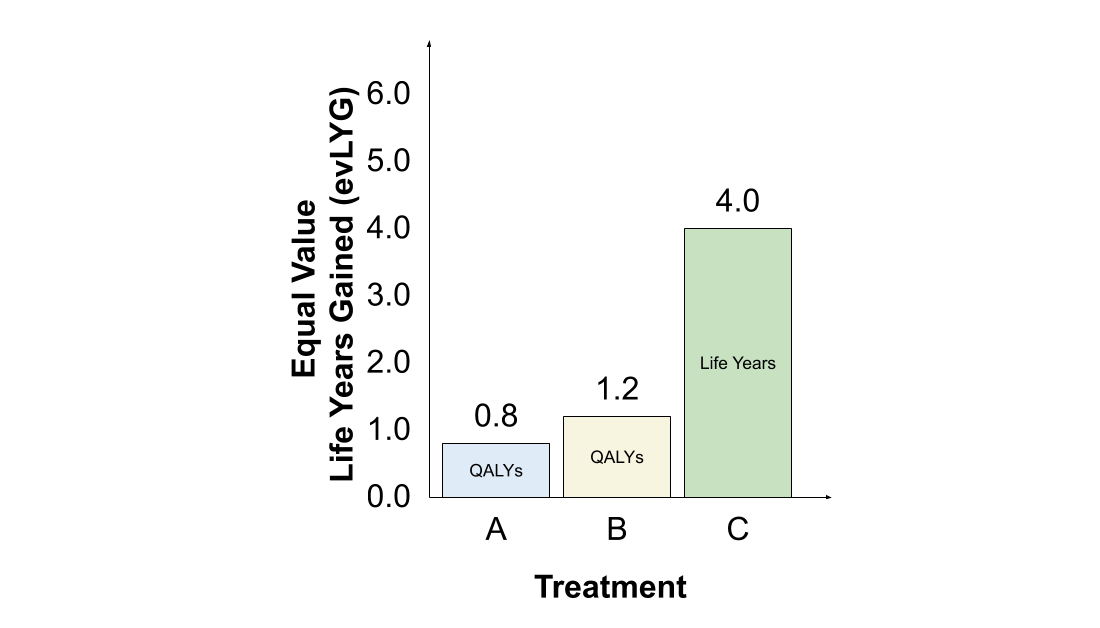
The #evLYG approach similarly assigns greater value to treatment B. When compared to & #39;current treatment& #39; A, the additional year of life expectancy with B is valued in full, while the first year is valued at the HRQoL (0.6), for a total of 1.6 evLYG. The value of A is 0.8 evLYG.
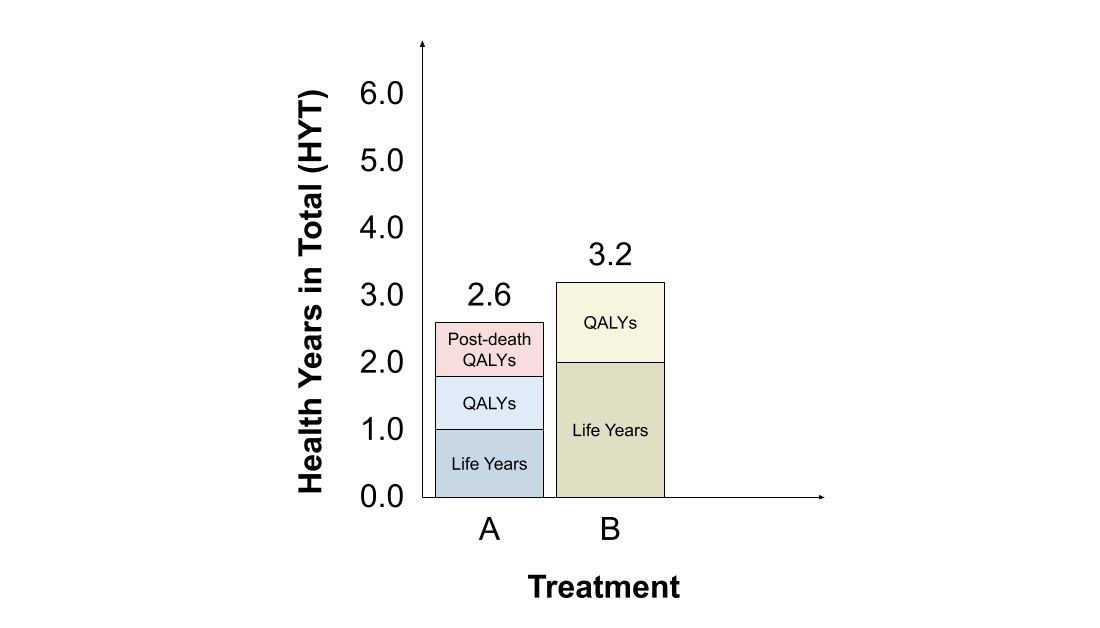
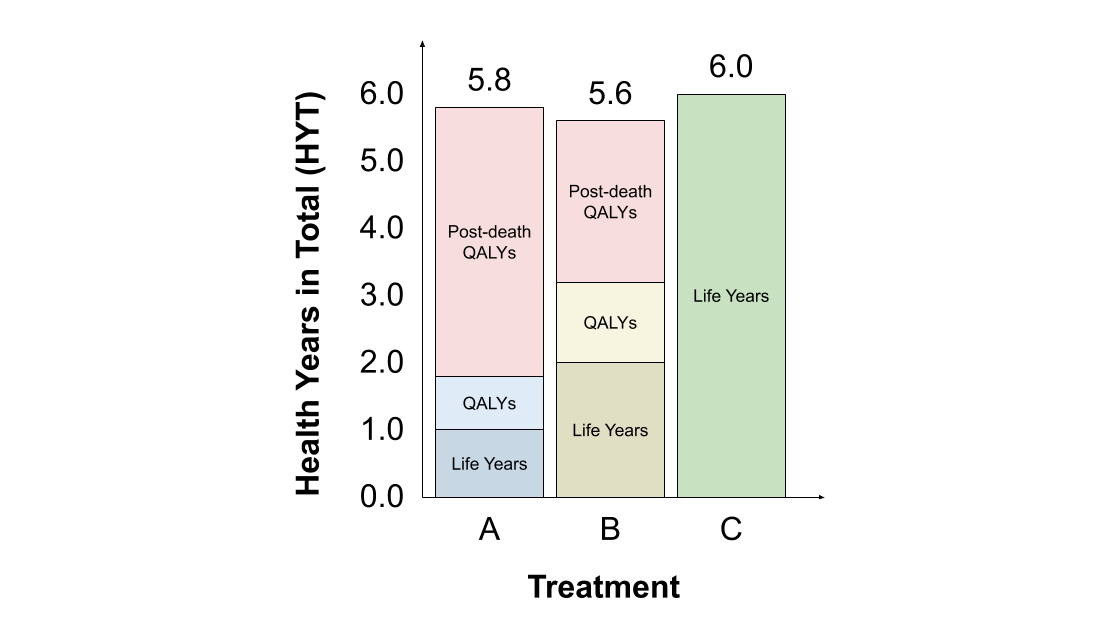
Finally, the #HYT also assigns greater value to treatment B. For B, 2 life years are added to 1.2 QALYs, for a total of 3.2 HYT. For A, 1 life year is added to 0.8 QALYs, and then 0.8 & #39;post-death QALYs& #39; are added (since life expectancy with B is 2 years), for a total of 2.6 HYT.
As a result, when we compare A and B alone, all four approaches favour treatment B. Now let& #39;s consider what happens if we introduce treatment C, which provides 6 years of life expectancy but with a HRQoL of zero.
Before we continue, it& #39;s worth bearing in mind that there are several different ways that a HRQoL of zero might arise in someone still alive. One would be if a patient is not sufficiently conscious to experience any & #39;health-related quality& #39; to their life, such as being in a coma.
Another would be if a patient& #39;s baseline HRQoL was & #39;worse than death& #39; and treatment then improved this to zero. A third would be if a patient& #39;s baseline HRQoL was positive but treatment toxicity reduced this to zero. These are just a few examples - I& #39;m sure there are many more.
So, how does each of these four approaches respond to us adding treatment C into the comparison?
Let& #39;s start with the #QALY. Since treatment C provides zero HRQoL, it& #39;s assigned no value regardless of its life expectancy. Treatment B remains the most desirable treatment, followed by treatment A.
The #LY favours switching to treatment C. Each year with C is valued the same as each year with treatment A or B, even though A and B provide positive HRQoL to patients and C does not. Treatment C provides for the longest life, which is all that matters under the #LY approach.
The #evLYG also favours switching to treatment C. The 4 additional years of life expectancy with treatment C compared to treatment B are valued in full, while the first 2 years are valued using QALYs (but are assigned zero value, since HRQoL is zero), resulting in 4.0 evLYG.
However, the #evLYG is dynamically inconsistent. If this comparison were repeated in future after treatment C has been established as & #39;current care& #39; (perhaps in response to a new treatment D), treatment C would be valued using QALYs only and the #evLYG would rank B higher than C.
Finally, the #HYT favours treatment C. Although its HYT comprise LYs only, these are sufficient to outweigh the total LYs, QALYs and & #39;post-death QALYs& #39; assigned to A and B. Also, treatment A is now preferred to B, due to the change in the & #39;reference& #39; strategy to treatment C.
In summary, only the #QALY necessarily favours a treatment that provides positive HRQoL to patients over those that do not. As this example shows, the other three approaches ( #LY, #evLYG and #HYT) can favour a treatment with a HRQoL of zero over treatments with positive HRQoL.
A related issue is that of treatments with *negative* HRQoL. This is a controversial subject: see @ChrisSampson87& #39;s research on & #39;states worse than death& #39; and @waq0r& #39;s recent paper on issues that can arise with the #QALY https://bitowaqr.github.io/files/qalyisableist.pdf">https://bitowaqr.github.io/files/qal...
Yet it is worth noting that two of these approaches ( #LY and #evLYG) would favour treatment C even if it had a substantially *negative* HRQoL. The #HYT can also favour treatments with negative HRQoL if life expectancy is sufficiently long (since the LYs overwhelm the QALY loss).
This issue does not arise with the #QALY. For all its faults, there are no circumstances under which the #QALY favours prolonging a patient& #39;s suffering in a state of extreme pain or other unbearably poor health over a treatment which provides for a shorter life of good health.

 Read on Twitter
Read on Twitter