The Infinite Pattern That Never Repeats by @veritasi

This is a pattern that was thought impossible, and a material that wasn't supposed to exist.

Here are my notes:

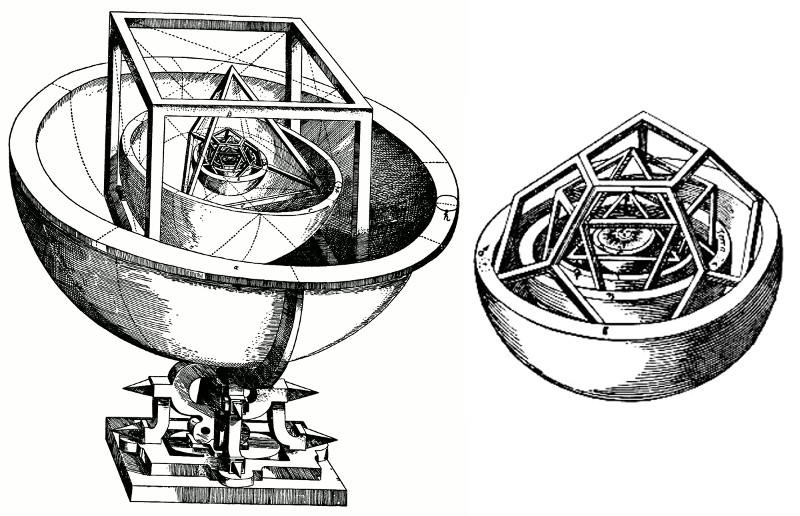
Johannes Kepler was a mathematician who theorised that the shapes of planetary orbits are ellipses, and he had this cool model of the solar system where spheres are separated by Platonic Solids

https://thatsmaths.com/2016/10/13/keplers-magnificent-mysterium-cosmographicum/

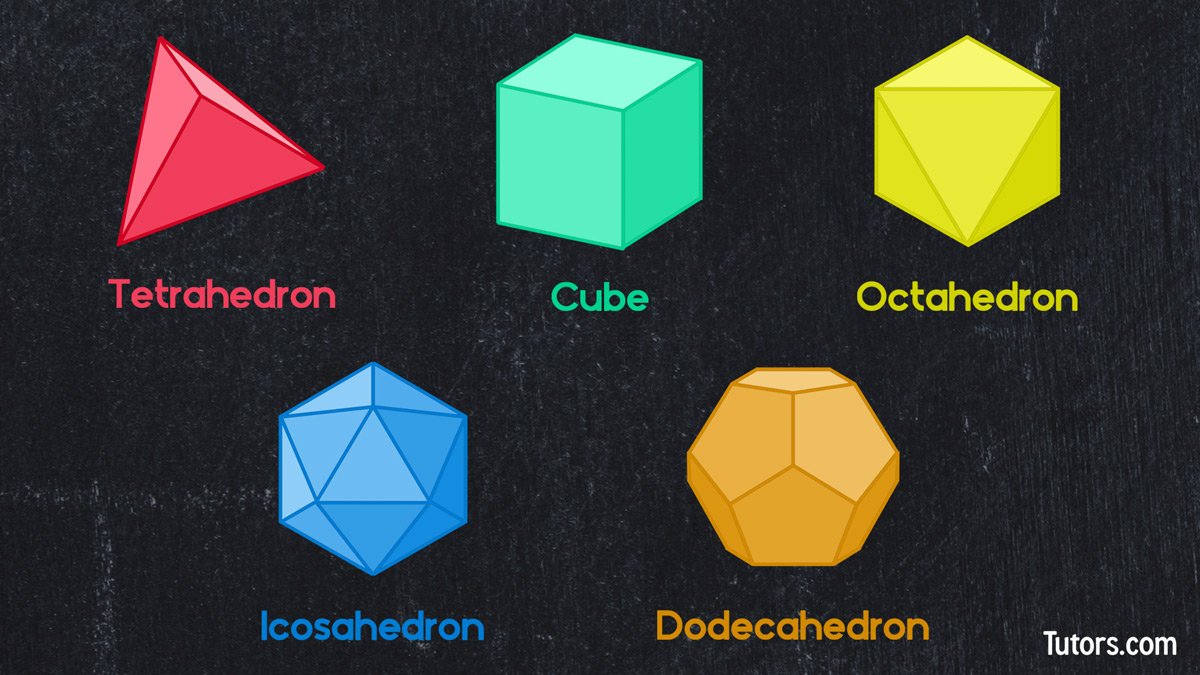
Platonic Solids are objects which faces and vertices are identical:
Cubes, Tetrahedons, Octahedons, Dodecadhedron, Isocahedron.

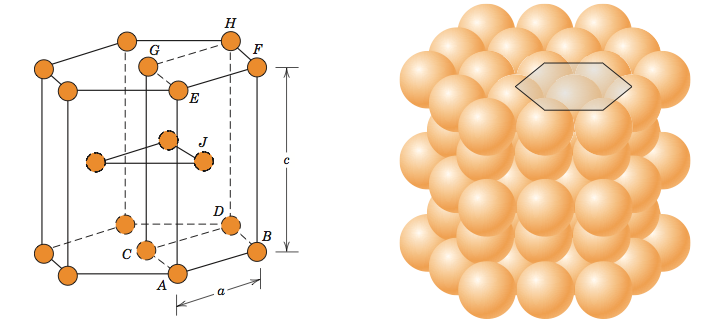
He was pondering on how to stack cannonballs so that they take up the least space on a ship's deck
The answer came in Hexagonal Close-Packing and Face Centred Cubics. They were both equally optimal in maximising use space.

At the same time, he was also observing snowflakes. Why are snowflakes always six-cornered?

With this he speculated about the hexagonal crystals, and the links between the patterns of snowflakes and the patterns of stacking cannonballs

A little bit of the math blew past my head in the middle, given that I don't know shit about geometry and math and patterns.

But Kepler knew that on a one-dimensional plane, hexagons can tile the plane periodically.

Periodic Tiling is when you can take a shape and you can duplicate it infinitely

Periodic patterns can have symmetry when you rotate the patterns, they look the same on different folds.
But it was strange because, you could only have symmetry on two, three, four and six-fold.

There are an infinite number of shapes that can tile the plane periodically
The hexagon can ONLY tile the plane periodically
Also an infinite number of shapes that can tile the plane periodically or non-periodically

Isosceles Triangles are periodic, but when you rotate them they become non-periodic

Same goes for Sphinx tiles in different arrangements

Hao Wang proposed that within his set of Wang Tiles if they can tile the plane, they can do so periodically, but this was disproved by his student Robert Berger

Which revealed that his tiles were actually Aperiodic (ONLY tile non-periodically)

https://en.wikipedia.org/wiki/Wang_tile 

There came an era of smart math people one-upping each other by getting their sets of aperiodic tiles smaller and smaller
Notably Raphael Robinson who came up with 6 Tiles that could tile the entire plane without repeating

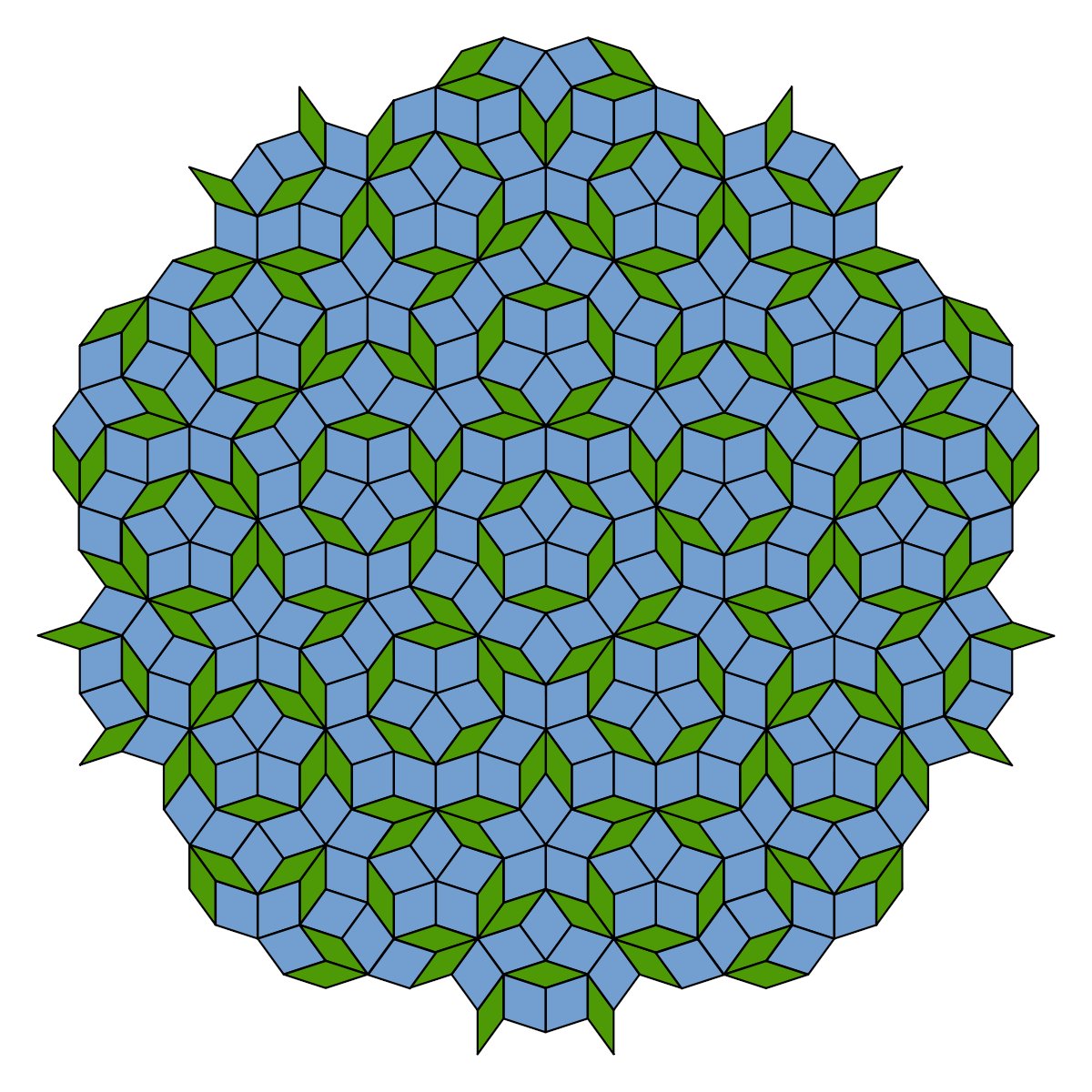
Roger Penrose ultimately brought that number to 2.
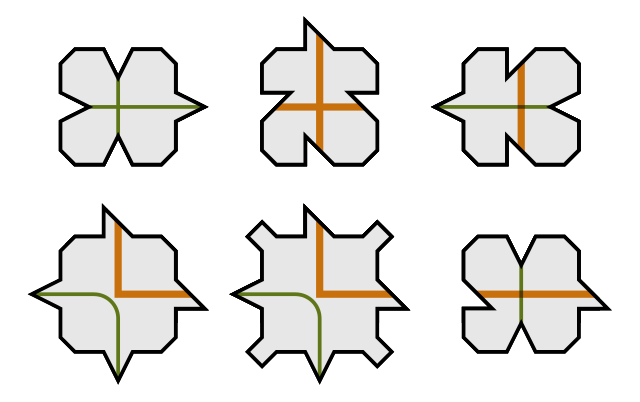
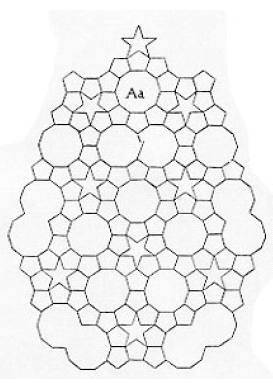
Starting with a pentagon, he dissected the shapes into smaller pentagons, and he found that by doing this, you can achieve a five-fold symmetry

The Penrose pattern matched Kepler's original pattern on five-fold symmetry that he wasn't able to prove

meaning that: the Penrose pattern was able to prove Kepler's original pattern using a different shape

Another bunch of math stuff about how the Penrose tiling can be broken down into the Golden Ratio and Fibonacci Sequences but I don't understand math

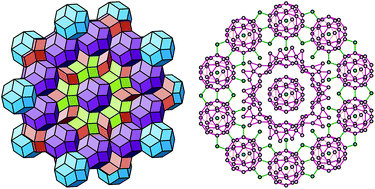
But because of Penrose Tilings, and a new understanding of five-fold symmetry, Paul Steinhardt and team were able to create a new kind of structure: quasicrystals.

Local rules were strong enough to allow a quasicrystal to reach a pattern infinitely.

which basically, if you are trying to create a Penrose Tiling, follow the rules of the vertices and you need to work one thing at a time. Two things simultaneously would ruin the pattern.

Quasicrystals have since been used to form dodecahedron shapes, for application of non-stick cookware and electrical steel

What exists that we cannot receive just because we thought it was impossible? Geometrics shapes looked so obvious that no one thought to look beyond them. And what we found were patterns that were both beautiful and counterintuitive.

There are materials that existed all along, that we just couldn't see for what they really are

I really loved this video because I learnt a lot about shapes and patterns, and inspired me to look past my own biases. There are so many things out there in the world we haven't explored yet, and there are still so many rules to the game we haven't discovered yet!

This was such a good video, thank you @veritasium
Do give it a like friends if you enjoyed it!