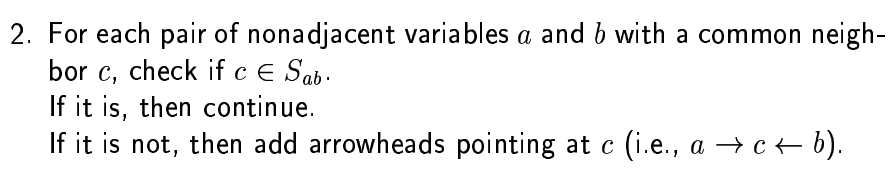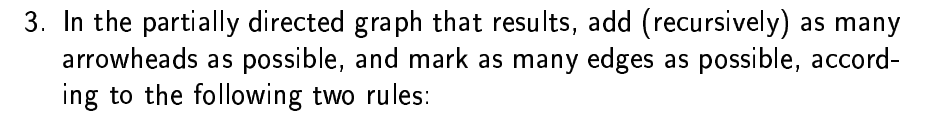Identifying Causal Structure in Your Data
- Helpful if you want to leverage the "Back-Door Adjustment" in order to robustly quantify the effects a variable X has on another Z
- This thread will be highlighting 2 great posts on #causality by @akelleh
/1
- Helpful if you want to leverage the "Back-Door Adjustment" in order to robustly quantify the effects a variable X has on another Z
- This thread will be highlighting 2 great posts on #causality by @akelleh
/1
Before jumping into the technical tools, I want to callout that they aren& #39;t perfect.
And when developing a causal graph I& #39;d encourage you to use them to help you, not do the job for you.
Be sure to leverage your intuitions and the intuitions of SMEs in addition to this tool.
/2
And when developing a causal graph I& #39;d encourage you to use them to help you, not do the job for you.
Be sure to leverage your intuitions and the intuitions of SMEs in addition to this tool.
/2
Causal Graph Inference by @akelleh
- Will be the first post we dive into
- Which explains how to use the IC* algorithm in practice
- Then we& #39;ll discuss the theory of the IC* algorithm
https://medium.com/@akelleh/causal-graph-inference-b3e3afd47110
/3">https://medium.com/@akelleh/...
- Will be the first post we dive into
- Which explains how to use the IC* algorithm in practice
- Then we& #39;ll discuss the theory of the IC* algorithm
https://medium.com/@akelleh/causal-graph-inference-b3e3afd47110
/3">https://medium.com/@akelleh/...
Say we have these 2 graphs and we want to understand the genuine causal relationships between these variables.
- Notice on the left X4 => X5 and on the right X4 and X5 will be correlated but there is no causality there
/4
- Notice on the left X4 => X5 and on the right X4 and X5 will be correlated but there is no causality there
/4
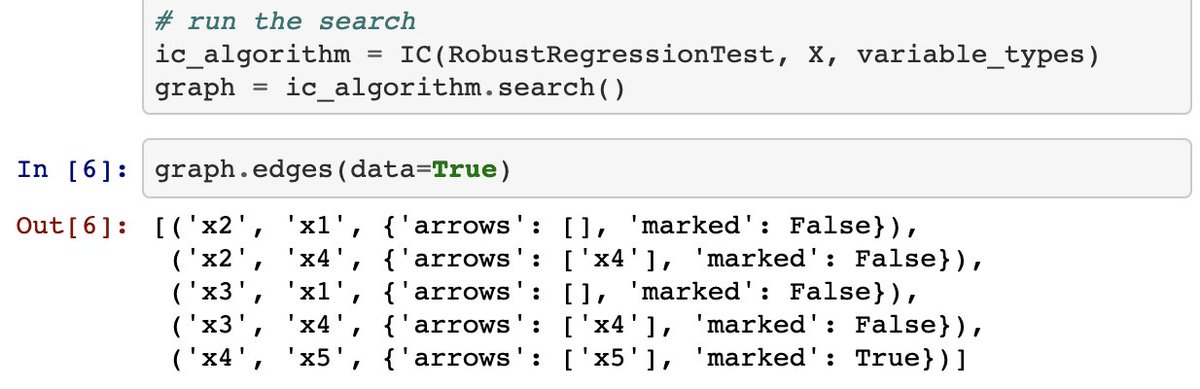
First we& #39;ll build the left graph and evaluate it.
- Inspecting results: it did a decent job: finding 3/5 of relations, no incorrect ones, and verified one is a genuinely causal (X4->X5)
- We use the IC* algorithm from @akelleh& #39;s causality package here: https://github.com/akelleh/causality
/5">https://github.com/akelleh/c...
- Inspecting results: it did a decent job: finding 3/5 of relations, no incorrect ones, and verified one is a genuinely causal (X4->X5)
- We use the IC* algorithm from @akelleh& #39;s causality package here: https://github.com/akelleh/causality
/5">https://github.com/akelleh/c...
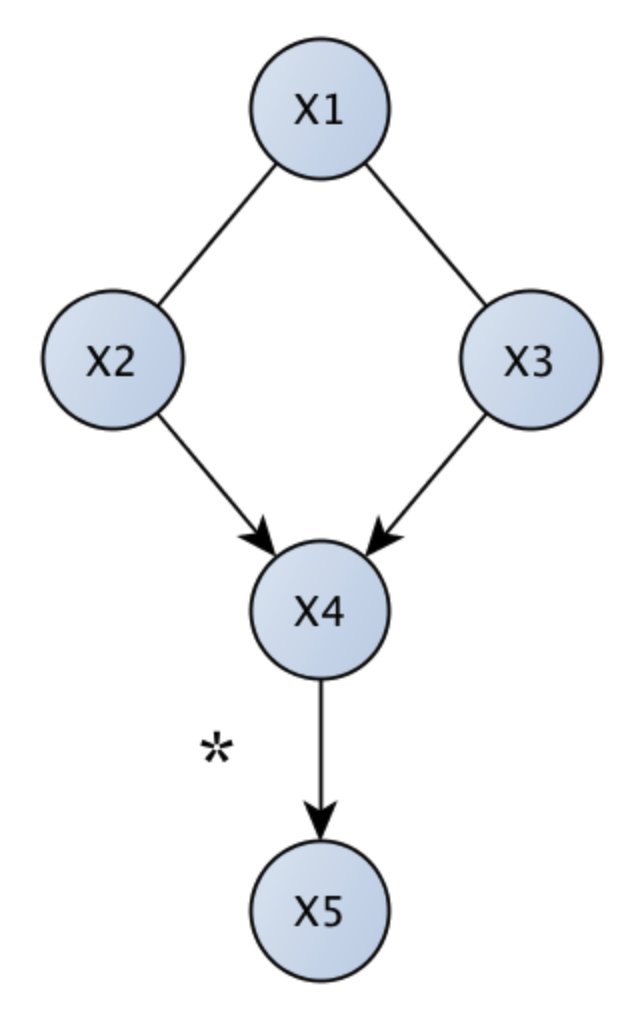
Now the right graph
- "[Algorithm] found that X4 and X5 are still correlated in a way that can’t be explained away by the data, but no longer can establish genuine causation."
- "pretty good, considering that there’s a latent confounding variable between X4 and X5 (X6)!"
/6
- "[Algorithm] found that X4 and X5 are still correlated in a way that can’t be explained away by the data, but no longer can establish genuine causation."
- "pretty good, considering that there’s a latent confounding variable between X4 and X5 (X6)!"
/6
IC* Algorithm
Now I& #39;ll be going into weeds a little more on the IC* Algorithm.
IC* is preferred over IC when you have latent variables (don& #39;t have all the variables)
Based on 2.6 of "Causality" by Judea Pearl
(Which is "the book" on causality)
http://bayes.cs.ucla.edu/BOOK-2K/book-toc.html
/6">https://bayes.cs.ucla.edu/BOOK-2K/b...
Now I& #39;ll be going into weeds a little more on the IC* Algorithm.
IC* is preferred over IC when you have latent variables (don& #39;t have all the variables)
Based on 2.6 of "Causality" by Judea Pearl
(Which is "the book" on causality)
http://bayes.cs.ucla.edu/BOOK-2K/book-toc.html
/6">https://bayes.cs.ucla.edu/BOOK-2K/b...
IC* Algorithm (Step 1)
For every pair of variables (a,b)
- If you can find a set of variables Sab that make a and b independent when you condition on them
- Then don& #39;t add an edge
- Else do
Bc if you can do this there must not be a genuine connection between these 2.
/7
For every pair of variables (a,b)
- If you can find a set of variables Sab that make a and b independent when you condition on them
- Then don& #39;t add an edge
- Else do
Bc if you can do this there must not be a genuine connection between these 2.
/7
IC* Algorithm (Step 2)
For every a,b without an edge, but have a common neighbour c:
- if c is in Sab (is in a path between them)
- then do nothing
- otherwise add arrows: a -> c <- b
Bc if c is not in the path between them, this is only way it could be their neighbour
/8
For every a,b without an edge, but have a common neighbour c:
- if c is in Sab (is in a path between them)
- then do nothing
- otherwise add arrows: a -> c <- b
Bc if c is not in the path between them, this is only way it could be their neighbour
/8
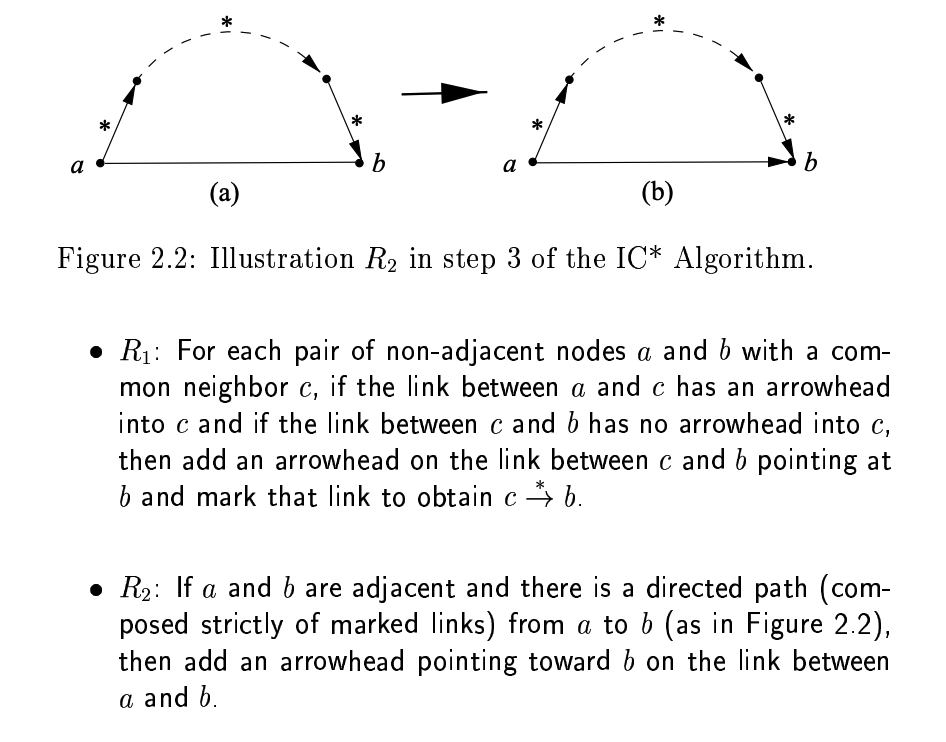
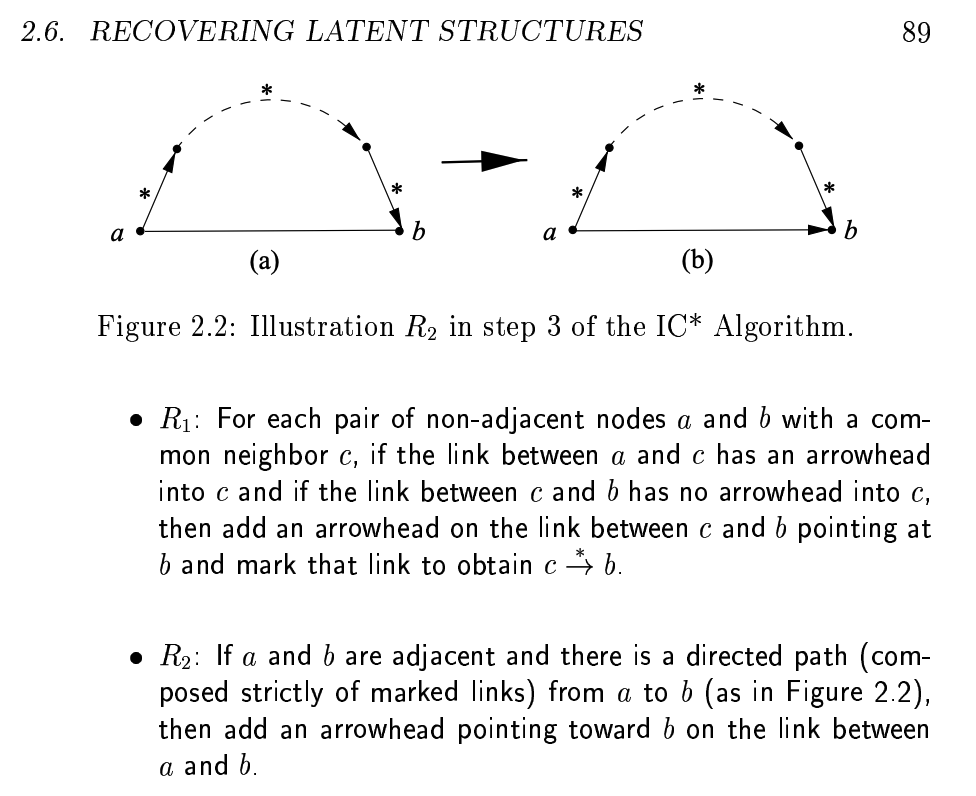
IC* Algorithm (Step 3)
For the resulting graph add (recursively) as many edge directions and significance as possible based on the rules:
- R1: if (a ->* c -> b) or (a ->* c - b) then (a ->* c ->* b)
- R2: if (a -> * ... ->* b) then (a -> b)
/9
For the resulting graph add (recursively) as many edge directions and significance as possible based on the rules:
- R1: if (a ->* c -> b) or (a ->* c - b) then (a ->* c ->* b)
- R2: if (a -> * ... ->* b) then (a -> b)
/9

 Read on Twitter
Read on Twitter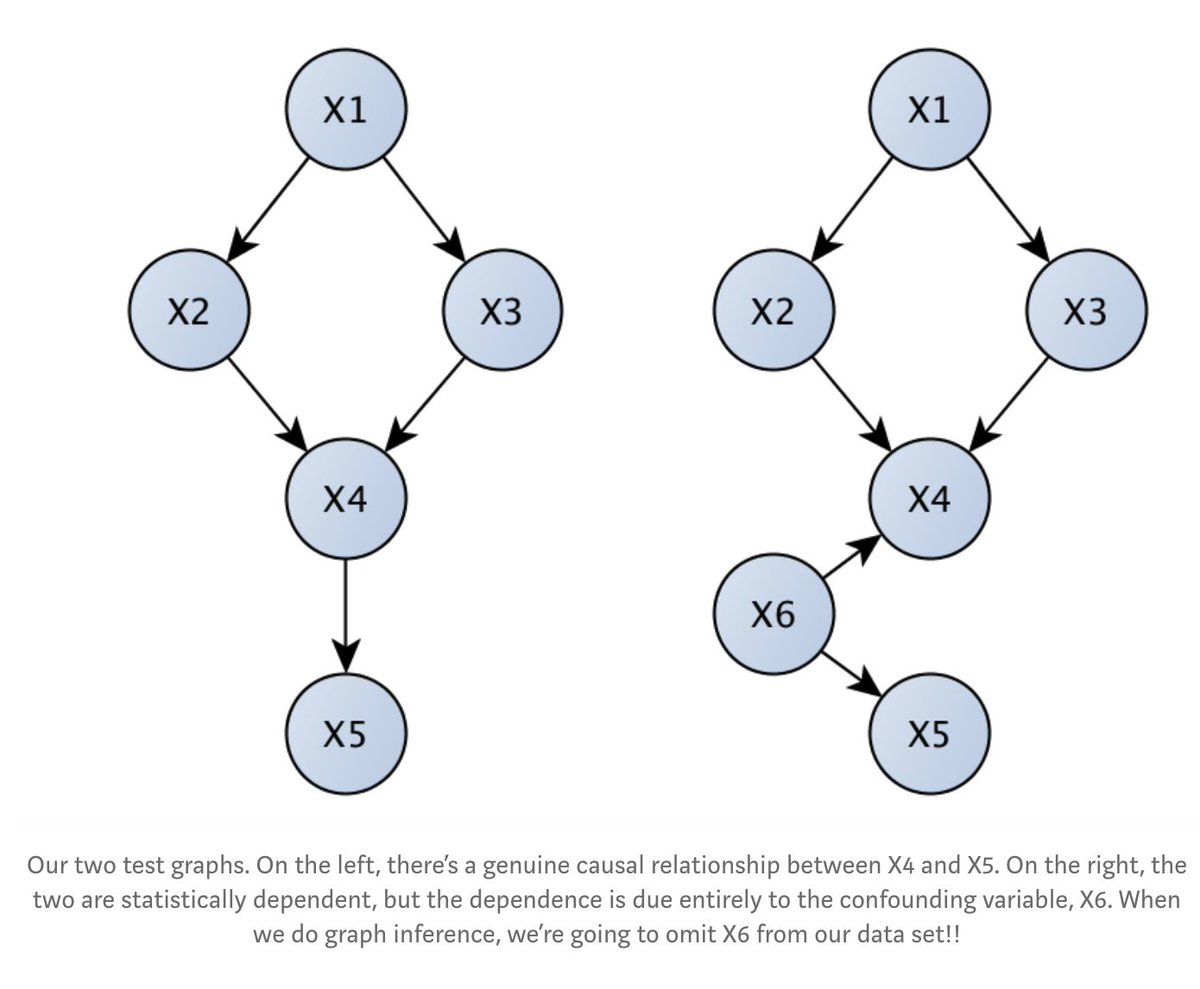

![Now the right graph - "[Algorithm] found that X4 and X5 are still correlated in a way that can’t be explained away by the data, but no longer can establish genuine causation."- "pretty good, considering that there’s a latent confounding variable between X4 and X5 (X6)!"/6 Now the right graph - "[Algorithm] found that X4 and X5 are still correlated in a way that can’t be explained away by the data, but no longer can establish genuine causation."- "pretty good, considering that there’s a latent confounding variable between X4 and X5 (X6)!"/6](https://pbs.twimg.com/media/EjbkFX8XcAExdwq.jpg)
![Now the right graph - "[Algorithm] found that X4 and X5 are still correlated in a way that can’t be explained away by the data, but no longer can establish genuine causation."- "pretty good, considering that there’s a latent confounding variable between X4 and X5 (X6)!"/6 Now the right graph - "[Algorithm] found that X4 and X5 are still correlated in a way that can’t be explained away by the data, but no longer can establish genuine causation."- "pretty good, considering that there’s a latent confounding variable between X4 and X5 (X6)!"/6](https://pbs.twimg.com/media/EjbkJkOWoAcAvjL.jpg)