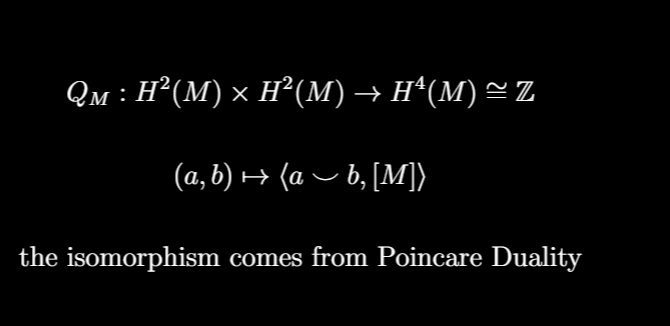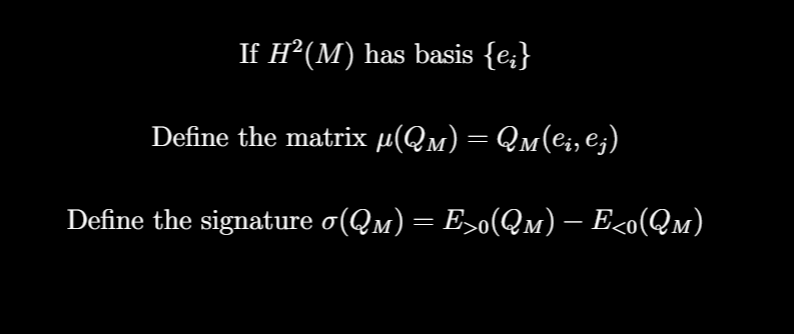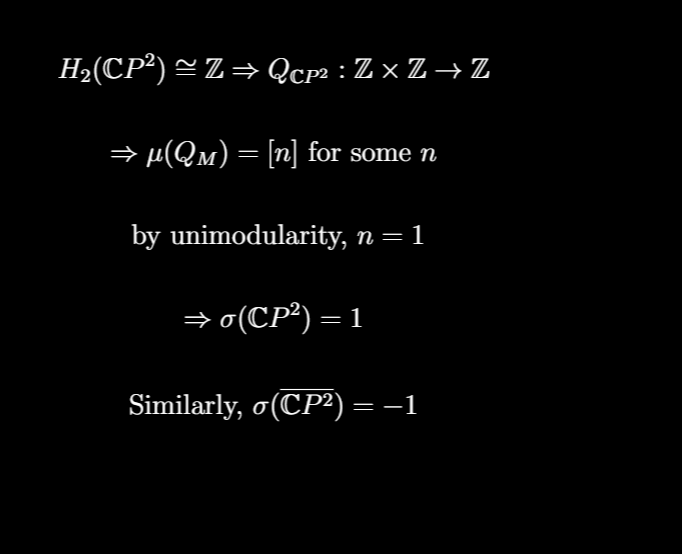~ thread ~ on computing the oriented cobordism group in degree 4! idk if this is how ppl normally do it, and some of these steps are my own, so i hope there aren& #39;t any mistakes  https://abs.twimg.com/emoji/v2/... draggable="false" alt="😁" title="Grinsendes Gesicht mit lächelnden Augen" aria-label="Emoji: Grinsendes Gesicht mit lächelnden Augen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="😁" title="Grinsendes Gesicht mit lächelnden Augen" aria-label="Emoji: Grinsendes Gesicht mit lächelnden Augen">
the (deg 4) oriented cobordism group is the set of oriented 4-folds with the disjoint union (or equivalently connect sum) making it a group under the equiv relat of oriented bordism: X ~ Y iff there is an oriented 5-fold M s.t. the boundary of M is the disjoint union of X and -Y
already this is unique from the unoriented case, where every element has 2-torsion (because you can just take M X [0,1] and flip the orientation)
the tool we need to see what this group is is called the intersection form: If M is closed, orientable, simply connected and connected 4-manifold, given two cocycles of degree 2, cup them together and evaluate against the fundamental class via Kronecker pairing:
In particular, we care about the signature of this form: Pick a basis of H^2(M) and represent Q_M as a matrix. Diagonalize it, and count the number of positive eigenvalues minus the number of negative eigenvalues. This turns out to be an important invariant.
another note about the matrix associated to Q_M: Using a combination of Poincare duality and universal coefficient theorem, we can show that \mu(Q_M) is unimodular, i.e. is invertible over the integers, i.e. has determinant 1 or -1.
It turns out that the signature is a complete bordism invariant (this is very difficult to prove), i.e. two manifolds have the same signature iff they are cobordant.
so the group of oriented cobordisms is isomorphic to the "group of signatures"! But what is that? There is an injective homomorphism to Z, but how do we know it is surjective? i.e. given an integer, how do we know there is a 4-manifold whose intersection form has that signature
with these two facts, it is clear that any signature can be obtained via connect summing copies of CP^2 and -CP^2, so the map is a surjection and we are finished.

 Read on Twitter
Read on Twitter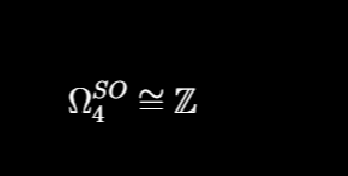 " title="~ thread ~ on computing the oriented cobordism group in degree 4! idk if this is how ppl normally do it, and some of these steps are my own, so i hope there aren& #39;t any mistakes https://abs.twimg.com/emoji/v2/... draggable="false" alt="😁" title="Grinsendes Gesicht mit lächelnden Augen" aria-label="Emoji: Grinsendes Gesicht mit lächelnden Augen">" class="img-responsive" style="max-width:100%;"/>
" title="~ thread ~ on computing the oriented cobordism group in degree 4! idk if this is how ppl normally do it, and some of these steps are my own, so i hope there aren& #39;t any mistakes https://abs.twimg.com/emoji/v2/... draggable="false" alt="😁" title="Grinsendes Gesicht mit lächelnden Augen" aria-label="Emoji: Grinsendes Gesicht mit lächelnden Augen">" class="img-responsive" style="max-width:100%;"/>