A technical question for the #DAG oracles of #EconTwitter, please.
How do we describe the bias created by conditioning on a variable that is *nearly* a necessary and sufficient condition for treatment?
It can falsely seem like a & #39;good control& #39;!
I& #39;ll explain in a short thread—>
How do we describe the bias created by conditioning on a variable that is *nearly* a necessary and sufficient condition for treatment?
It can falsely seem like a & #39;good control& #39;!
I& #39;ll explain in a short thread—>
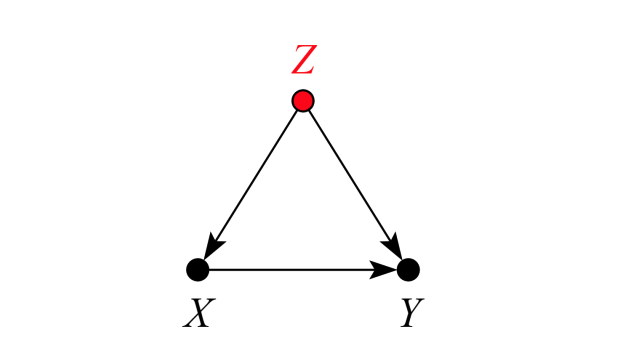
In general, conditioning on an omitted variable like Z in this DAG gives an unbiased estimate of the average treatment effect of X on Y.
Z is a "good control", in this figure from the excellent guide by @analisereal, Forney, and @YudaPearl —> https://ftp.cs.ucla.edu/pub/stat_ser/r493.pdf">https://ftp.cs.ucla.edu/pub/stat_...
Z is a "good control", in this figure from the excellent guide by @analisereal, Forney, and @YudaPearl —> https://ftp.cs.ucla.edu/pub/stat_ser/r493.pdf">https://ftp.cs.ucla.edu/pub/stat_...
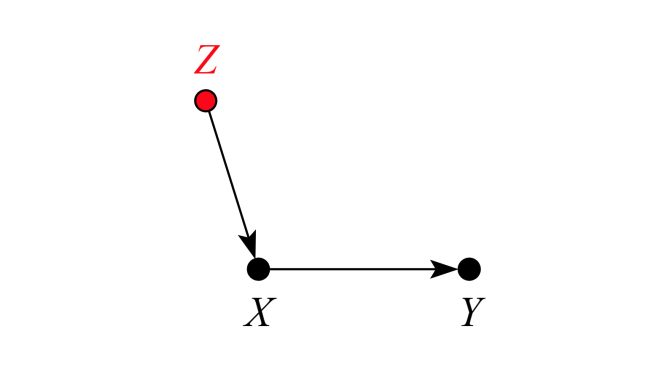
But suppose that Z is almost a necessary & sufficient condition for X.
E.g., we are studying the effect of schooling on test scores (Y). X is the completion of 6th grade. Z is the completion of *5th* grade.
The above DAG applies: both completing 5th and 6th grade affect scores.
E.g., we are studying the effect of schooling on test scores (Y). X is the completion of 6th grade. Z is the completion of *5th* grade.
The above DAG applies: both completing 5th and 6th grade affect scores.
But if I condition on the "good control" Z, I alter interpretation of the treatment effect E[Y|X=1] – E[Y|X=0].
Completing 5th grade is *almost* a necessary condition for completing 6th grade. (& #39;Almost& #39;, because a few very unusual kids might enter the system at grade 6.)
Completing 5th grade is *almost* a necessary condition for completing 6th grade. (& #39;Almost& #39;, because a few very unusual kids might enter the system at grade 6.)
Completing 5th grade is also *almost* a sufficient condition for completing 6th grade. (& #39;Almost& #39;, because a few very unusual kids might drop out of all schooling after grade 5.)
So if I study the effect of X on Y controlling for the & #39;good control& #39; Z, in this case I might well find that there is no general "effect" of completing 6th grade on scores.
But we sense that that would be a meaningless conclusion. If we condition on completing grade 5, the "effect" of X on Y is only the effect of being one of those highly unusual kids who enter or leave the system between grades 5 and 6.
That & #39;effect& #39; might be completely different than the average treatment effect of grade 6 in the whole population, precisely because those kids are so unusual.
It could even be zero. But that would be uninformative to a policymaker interested in the effect of 6th grade on scores.
It could even be zero. But that would be uninformative to a policymaker interested in the effect of 6th grade on scores.
So Z is not at all a & #39;good control& #39; in this case because it would not help us identify the effect we& #39;re interested in. Indeed it seems to take us very far away from the effect of interest.
So notwithstanding the DAG above, Z is a & #39;bad control& #39; here.
So notwithstanding the DAG above, Z is a & #39;bad control& #39; here.
This problem is closely related to @HeckmanEquation& #39;s point in his 2000 @QJEHarvard paper: https://doi.org/10.1162/003355300554674
Our">https://doi.org/10.1162/0... original claim that the effect of interest is the effect of X on Y implicitly assumes we can cause X to vary independently of Z. (X and Z are & #39;variation free& #39;.)
Our">https://doi.org/10.1162/0... original claim that the effect of interest is the effect of X on Y implicitly assumes we can cause X to vary independently of Z. (X and Z are & #39;variation free& #39;.)
It is *possible* for a few students to get a 6th grade education without getting a 5th grade education, and vice versa.
But that is a different "effect", Heckman writes, than the "effect" any policymaker would be interested in: the effect of "completing 5th and then 6th grade".
But that is a different "effect", Heckman writes, than the "effect" any policymaker would be interested in: the effect of "completing 5th and then 6th grade".
My question is: What is our terminology for this bias?
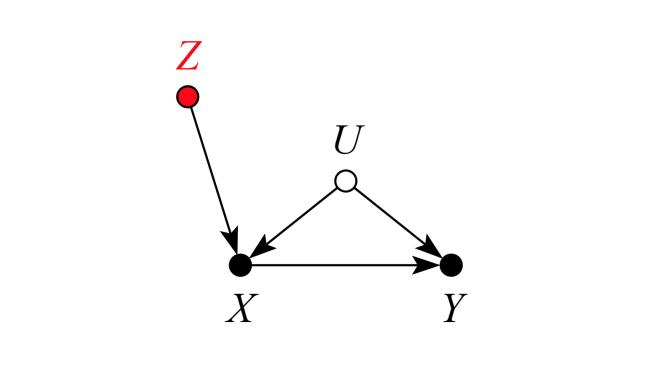
The problem is worse than just reducing the useful variation in X, and thereby reducing the *precision* of the estimated treatment effect, as in this & #39;neutral control& #39; case in the @analisereal, Forney, and @yudapearl paper.
The problem is worse than just reducing the useful variation in X, and thereby reducing the *precision* of the estimated treatment effect, as in this & #39;neutral control& #39; case in the @analisereal, Forney, and @yudapearl paper.
Rather, in the present case conditioning on Z means estimating the treatment effect only for a tiny and perhaps unrepresentative slice of the population.
Is this a form of "bias amplification"?
Is this a form of "bias amplification"?
If not, then what is the terminology we use to describe this bias?
Put differently, how do we analyze the bias created by conditioning on a *pre treatment* variable that is nearly a necessary and sufficient condition for treatment?
Put differently, how do we analyze the bias created by conditioning on a *pre treatment* variable that is nearly a necessary and sufficient condition for treatment?
I apologize if this is an ignorant question. (I am pretty sure it is.) But I am a newcomer to @yudapearl& #39;s monumental #BookOfWhy research program. If it is easy for you to see what I& #39;m missing, I& #39;d greatly appreciate a pointer. Thank you.
Update: I learned that essentially this problem is also called the "Table Two Fallacy" in this insightful piece by @EpidByDesign & @Lester_Domes —> https://doi.org/10.1093/aje/kws412
That">https://doi.org/10.1093/a... is, it might better be described as a "fallacy" than a "bias". Thank you (!) to all who commented.
That">https://doi.org/10.1093/a... is, it might better be described as a "fallacy" than a "bias". Thank you (!) to all who commented.

 Read on Twitter
Read on Twitter