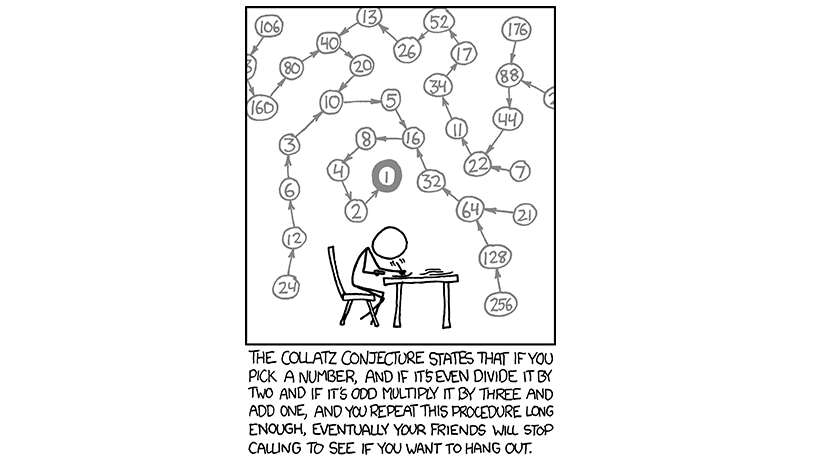
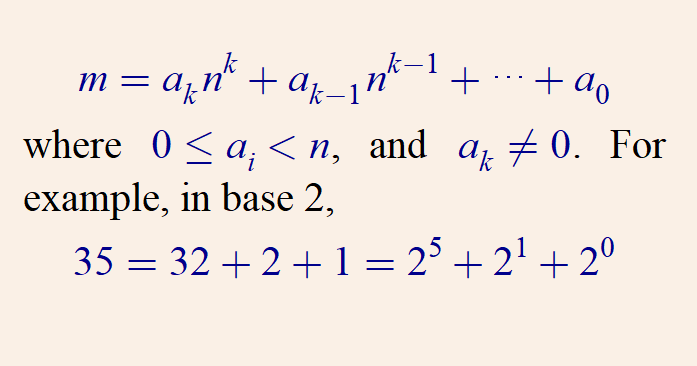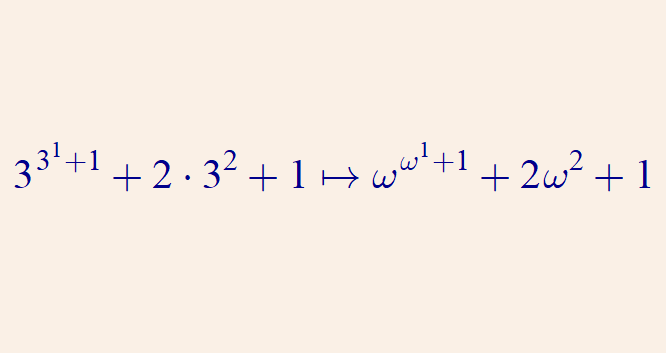1/ The famous Collatz conjecture asks if repeating the following on any number always ends in 1: if the number is even, half it; if odd, triple it & add 1. What if Collatz's neither true or false with our current axioms? In fact, here is an example of this for a similar problem!

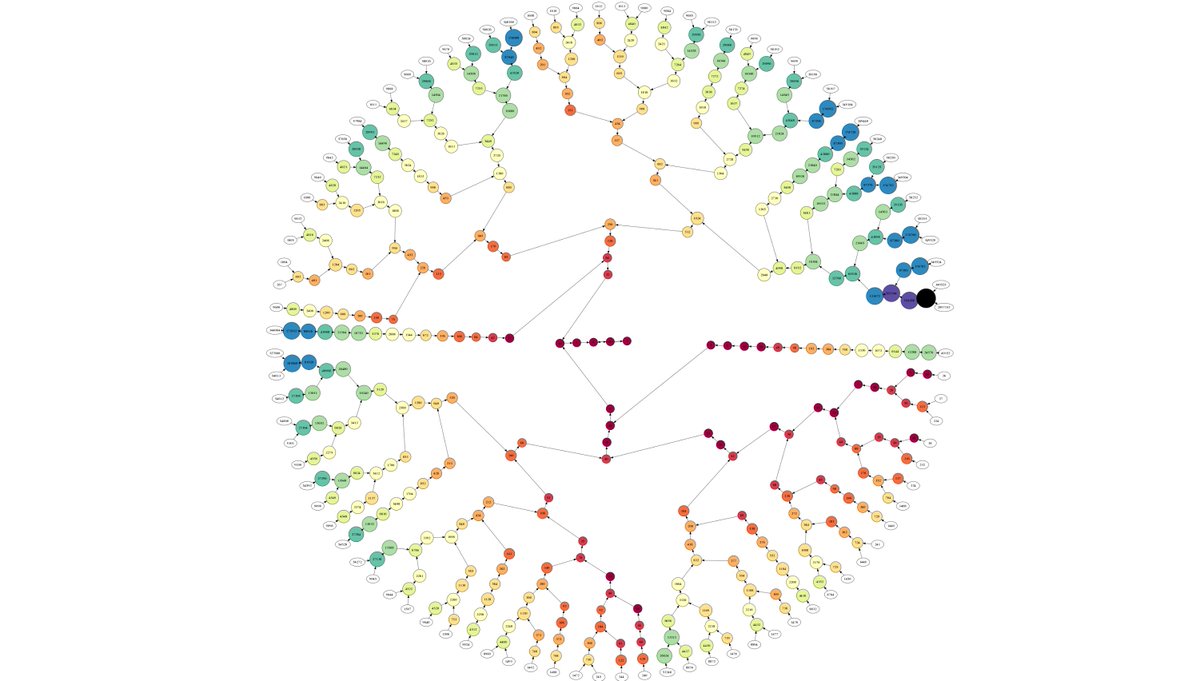
2/ The Goodstein sequence is one such instance: an integer sequence that always converges to 0 but *cannot be proven* to do so without assuming the existence of an infinity, which seems to have nothing to do with the sequence.

3/ Let me tell you what Goodstein sequence is. First I need to explain the notion of "hereditary base-n" notation. Now, in ordinary base-n notation, a number m is expressed as

4/ Here, the exponents themselves are not in base-n notation. In *hereditary* base-n notation, you want to express these exponents in base-n notation, and then the exponents of those exponents, and so on. For example,

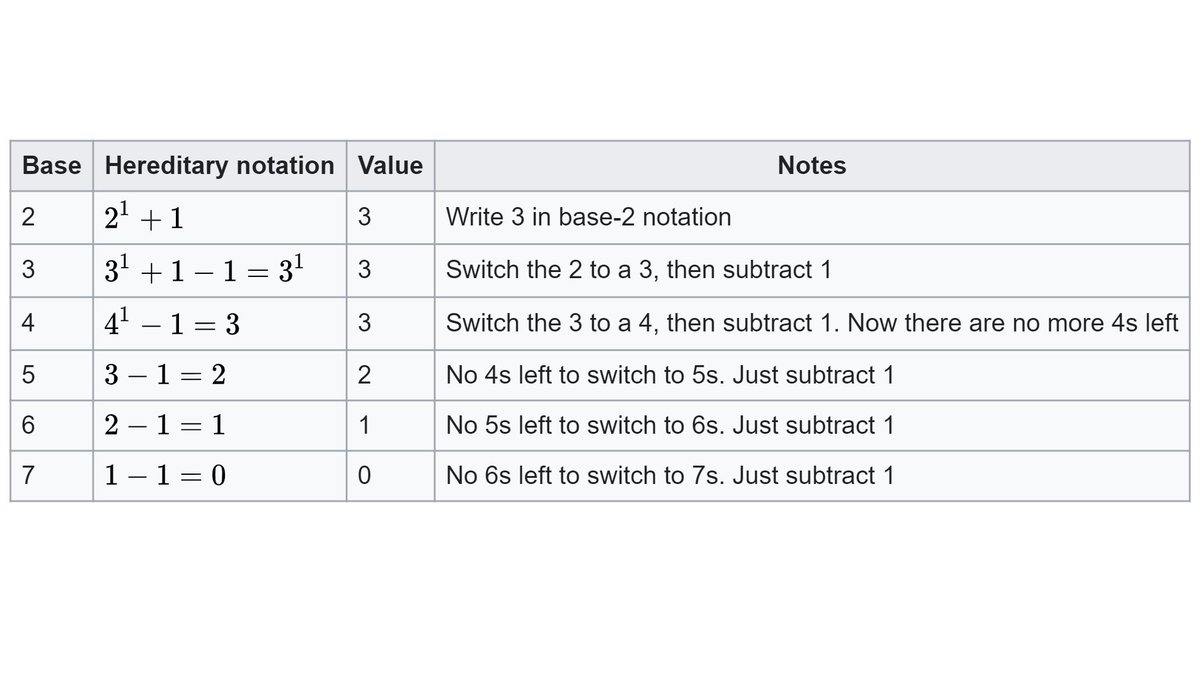
5/ Here's the defn of Goodstein sequence starting at m: First element of the sequence is m itself. Next, write m in "hereditary base-2 notation" & swap all 2s to 3s (in exponents too!). Finally subtract 1. This number is the next element of the sequence. (See below for example)

6/ Next, write this number in "hereditary base-3" notation, swap 3s to 4s, and subtract 1. This is the next number. In general, to get the k+1th element from the kth element, we write the former in hereditary base-(k+1), swap out all (k+1) with (k+2), then subtract 1.

7/ Here's an example for Goodstein sequence starting at m=3.

8/ Intuitively, this swapping of (k+1) with (k+2) exponentially increases the number in general, while subtracting 1 just weakly decreases the number, so it'd seem this sequence should increase to infinity indefinitely.

9/ But note that when the base is large, the number is below the base, so swapping (k+1) with (k+2) has no effect, and we end up subtracting 1 until it reaches 0.

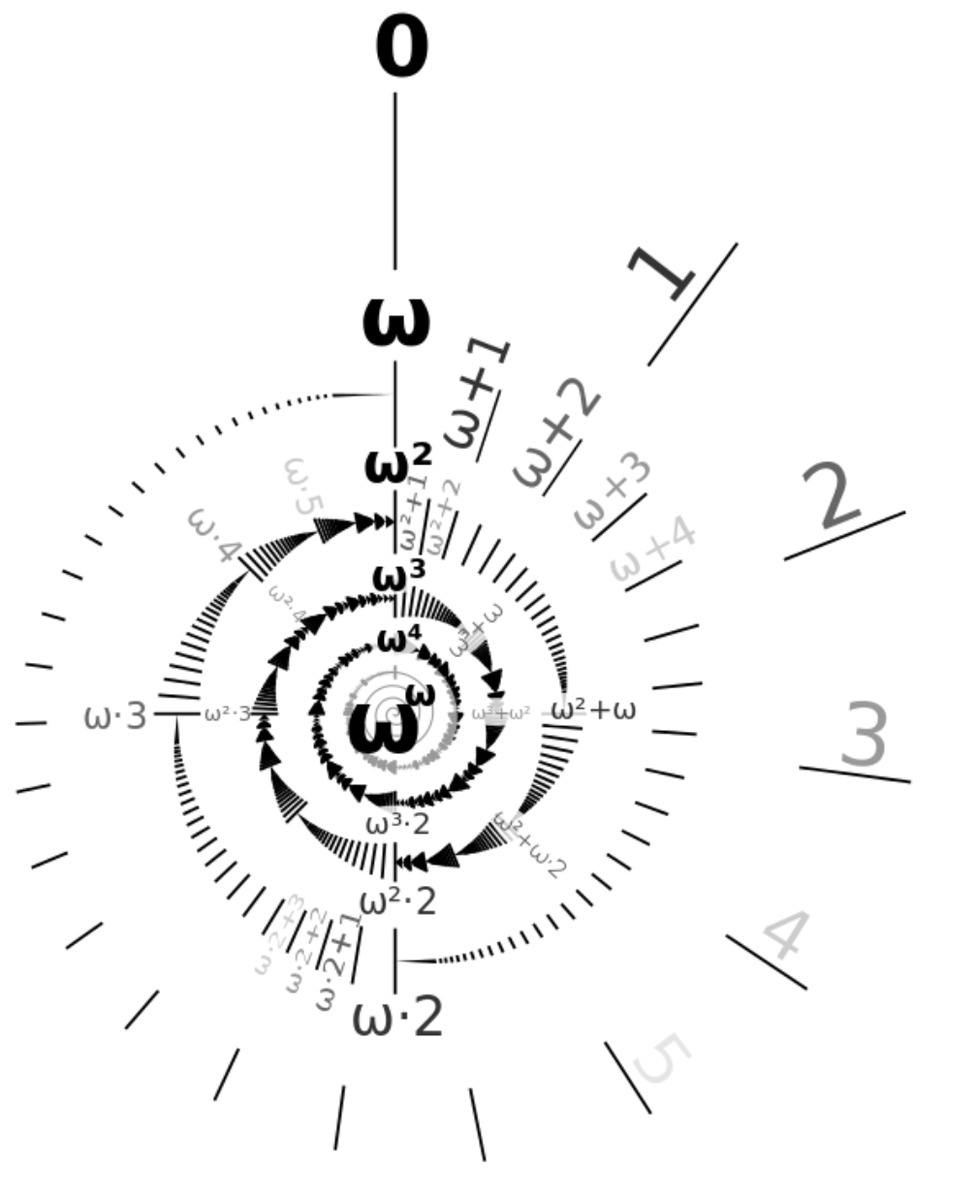
10/ A slick way of proving the convergence of Goodstein sequences uses "ordinal arithmetics". An ordinal is a measure of position of an element in an (infinite) sequence (contrast with "cardinals" which measure the "size" of a set). The natural numbers are ordinals, obviously.

11/ The first infinite ordinal is ω, representing the "limit" of all natural numbers. For example, imagine the sequence 1, 1/2, 1/3, 1/4, ... and let's tack on its "limit" 0 at the end. Then 1/n has position n, but 0 has position ω.

12/ Interesting, you can sum, multiply, and exponentiate ordinals just like you can with natural numbers. This will be important for the Goodstein sequence. You can read more about it here https://en.wikipedia.org/wiki/Ordinal_arithmetic.

13/ Back to Goodstein sequence: We construct a parallel sequence to the Goodstein sequence as follows: in every hereditary base-k representation, replace k with ω, the first infinite ordinal (the ordinal representing the set of natural numbers). For example:

14/ If you know ordinal arithmetics, then you can recognize that this parallel sequence always decreases due to the subtraction of 1. If the Goodstein sequence never terminates, then this parallel sequence of ordinals is an infinite sequence of descending ordinals

15/ This would violate what's known as the "well-founded property" of ordinals: there is no infinite sequence of descending ordinals. Thus this shows that the Goodstein sequence must terminate, and this happens only if it reaches 0.

16/ Now this proof used an infinite "number"/ordinal. As mentioned above, it turns out without using infinite numbers, you *cannot* prove this convergence! This is known as the Kirby-Paris theorem. It requires a lot more mathematical logic so I'll omit the details.

17/ I find this really interesting: a natural question purely about finite integers requires the existence of infinity for an answer. This suggests that innocent problems about simple things can really require us to assume seemingly unrelated assumptions

18/ As to the Collatz conjecture, I'm not sure if it will actually be independent from our current axioms. On the one hand, many people have tried and failed to solve it, so perhaps it is independent. On the other, plenty of similar problems have definite solutions, so *shrug*

19/ Credits: xkcd on collatz https://xkcd.com/710/  I used wikipedia https://en.wikipedia.org/wiki/Goodstein%27s_theorem a lot, with examples from there. Goodstein sequence is equivalent to a hydra game, and I used an image from https://www.semanticscholar.org/paper/Introduction-and-Proof-of-the-Goodstein-Sequence-Tigerschi%C3%B6ld/bdec90593d617cb23650fb8e55e0b8409da43b06. Ordinal image from https://en.wikipedia.org/wiki/Ordinal_number.

20/ And thanks to Nate Ackerman for telling me this cool result years ago!