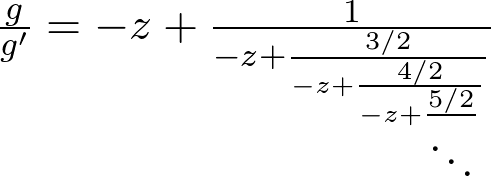Here& #39;s one way to guess it: There is (a little known?) continuation process for linear differential equations, where at each step f^(k)/f^(n+1) is introduced: https://twitter.com/johncarlosbaez/status/1299442096621760512">https://twitter.com/johncarlo...

This is possible, because at each stage, the derivative satisfies another linear equation, whose coefficients Q_k and P_k fulfill a "simple" recurrence.

The trick is to find such equation for the integral in question, for example:

This gives very simple coefficients of Q_k = -z/(k+1), P_k =1/(2k+2), and the fraction (after multiplying by denominators of Q):

Substituting for g(z) the integral reappears, and I hope you can manage the final tidying up of signs and fractions ;)
[End of Thread]