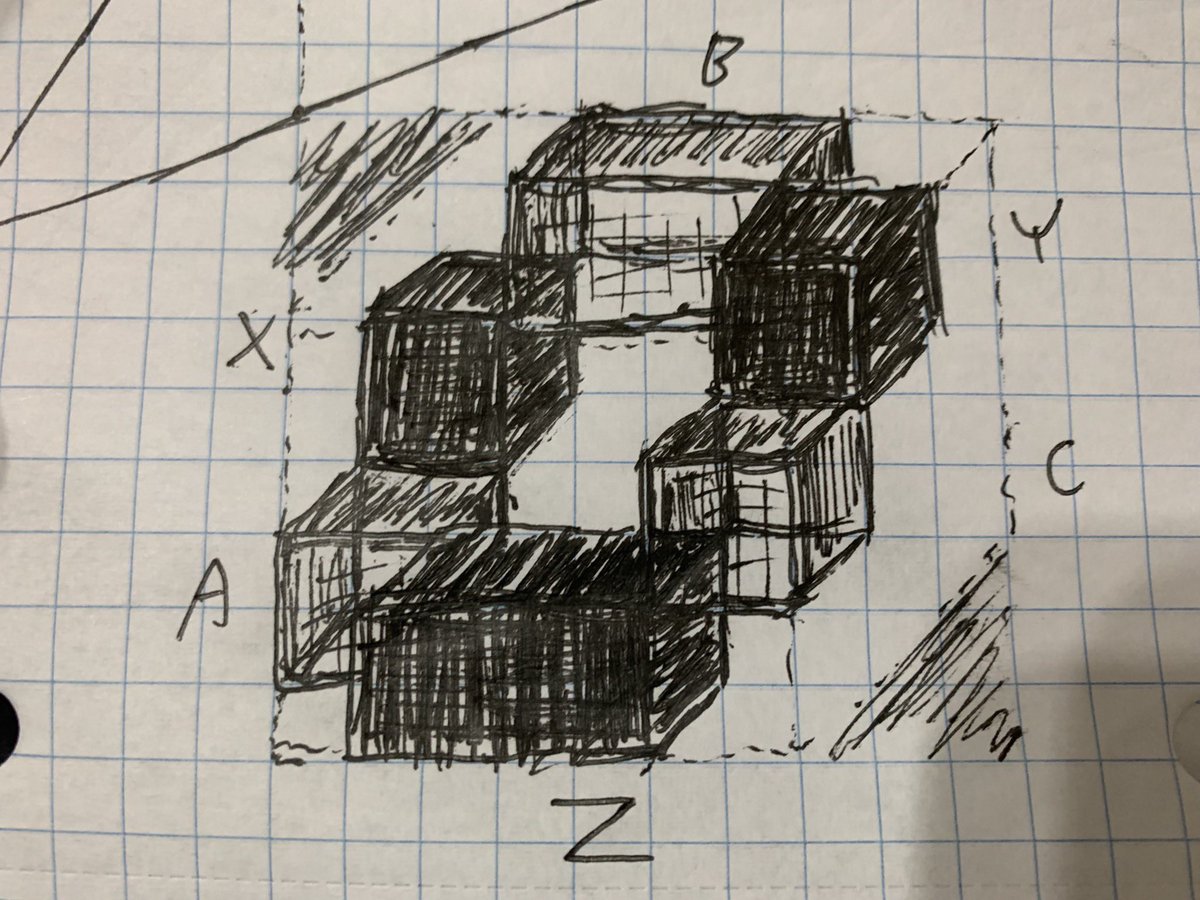
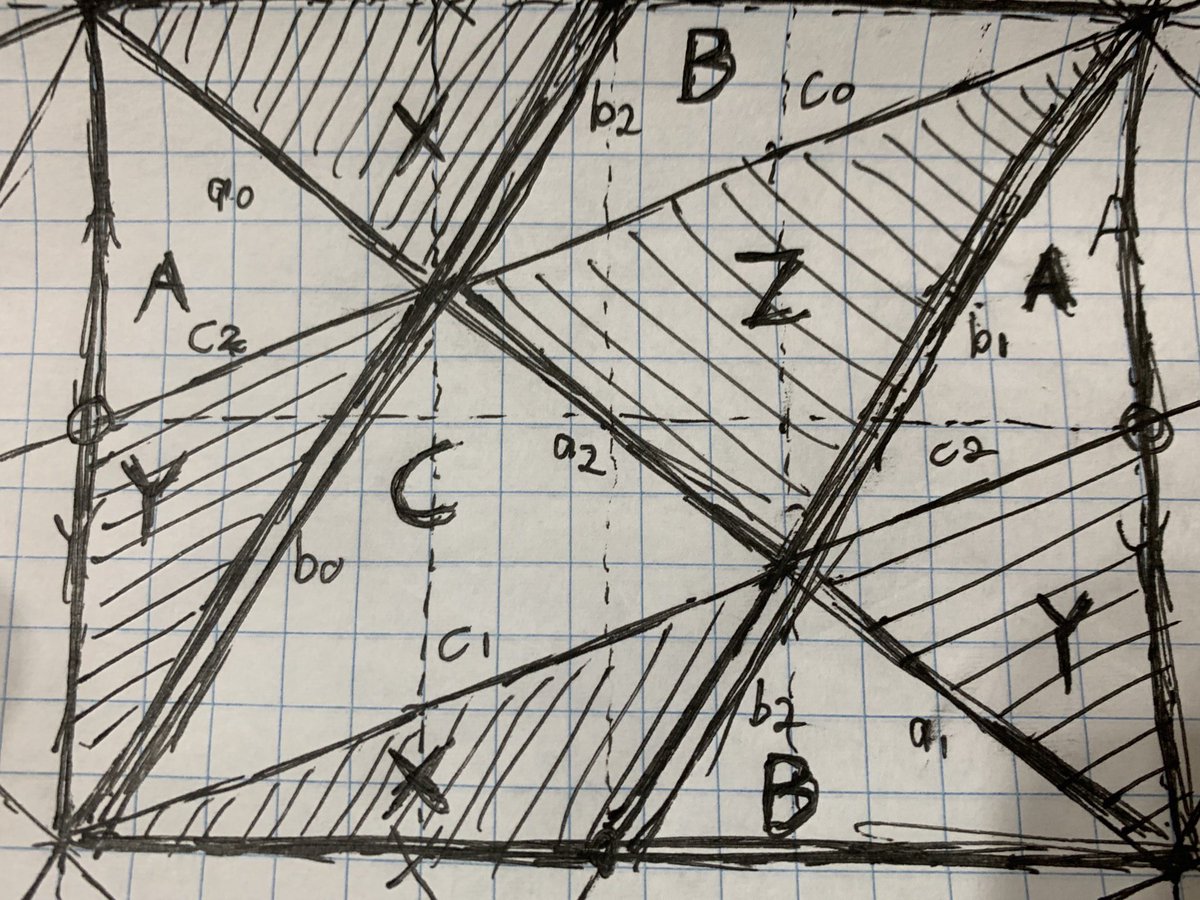
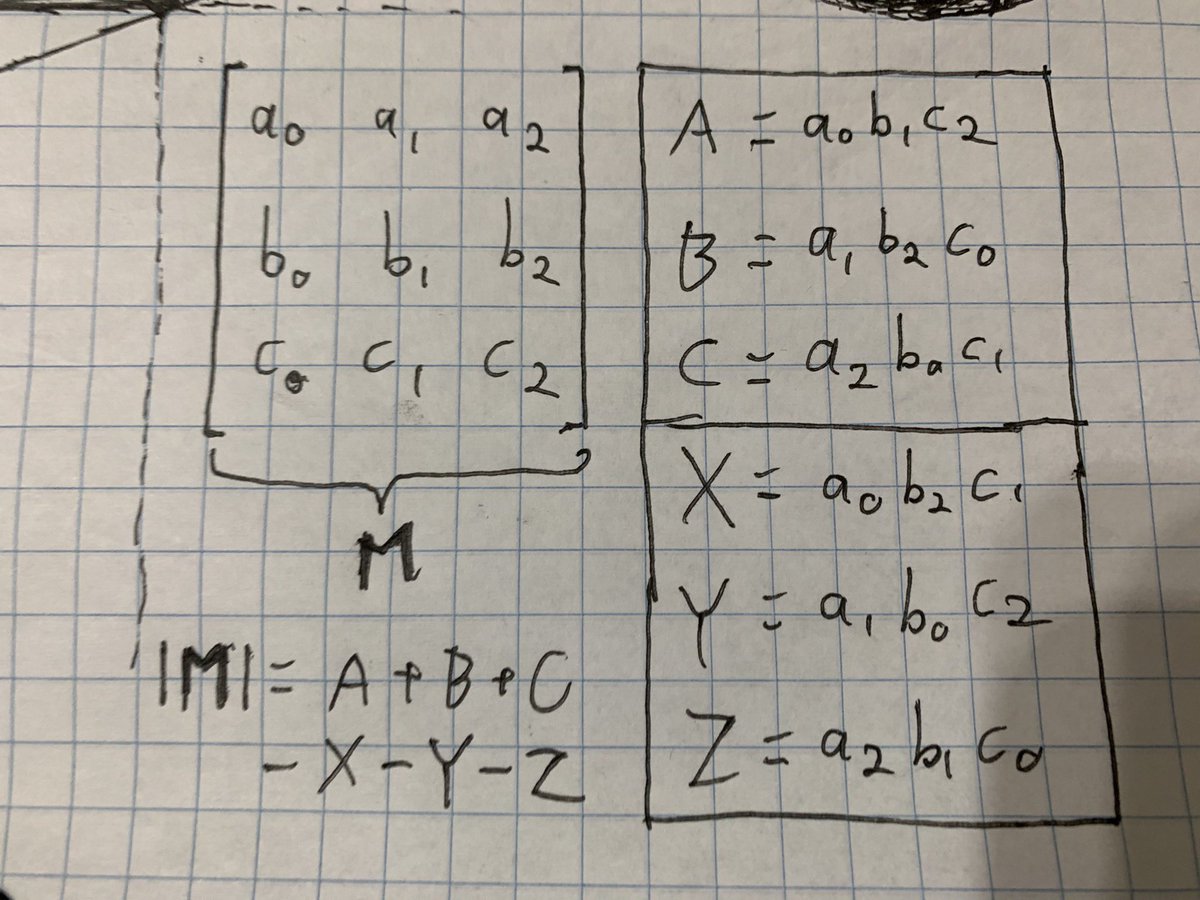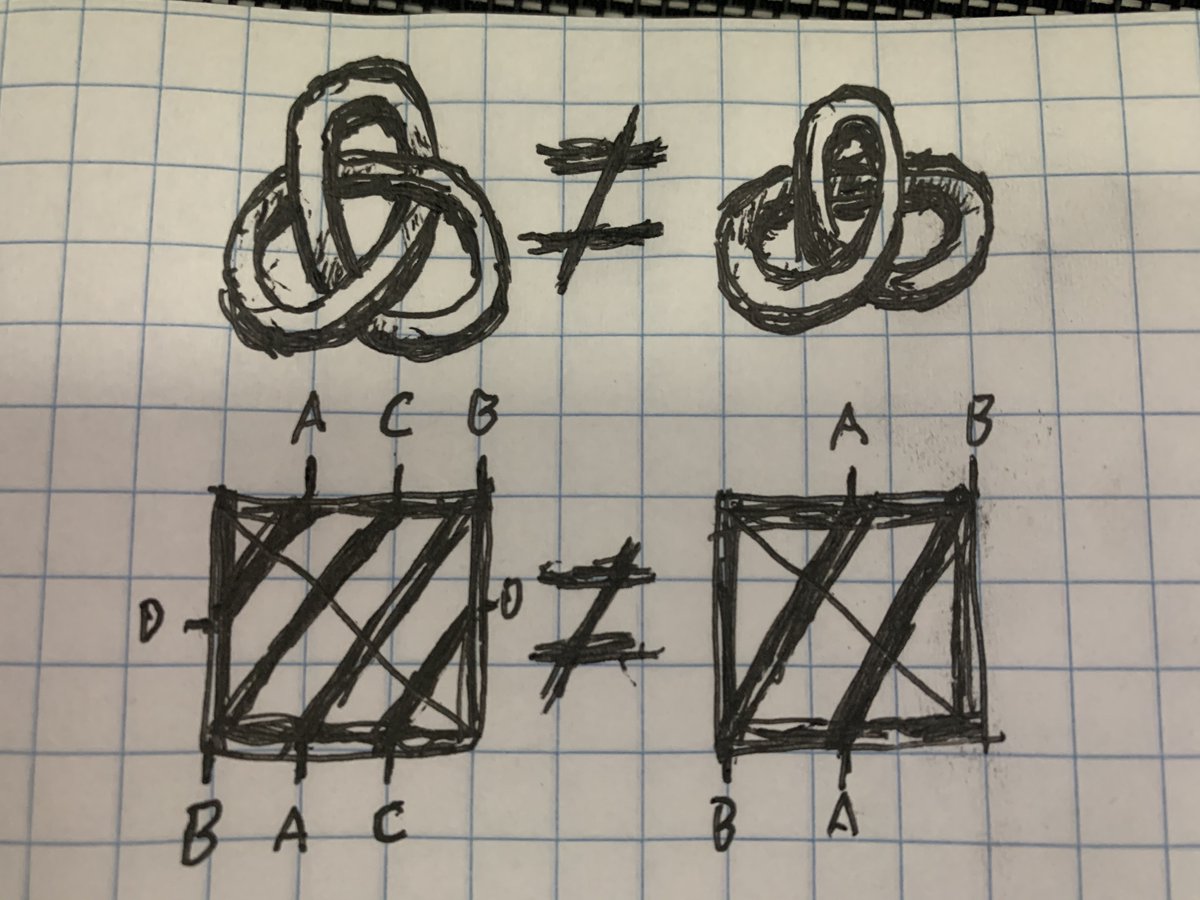So maybe found a tenuous connection between the structure of the determinant of a 3x3 matrix and the topology of the trefoil knot. 3 positive and 3 negative volumes contribute to the determinant. Each positive/negative pair shares a unique common factor.

(1/4)

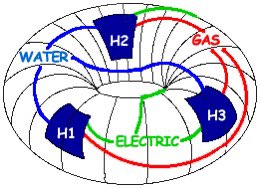
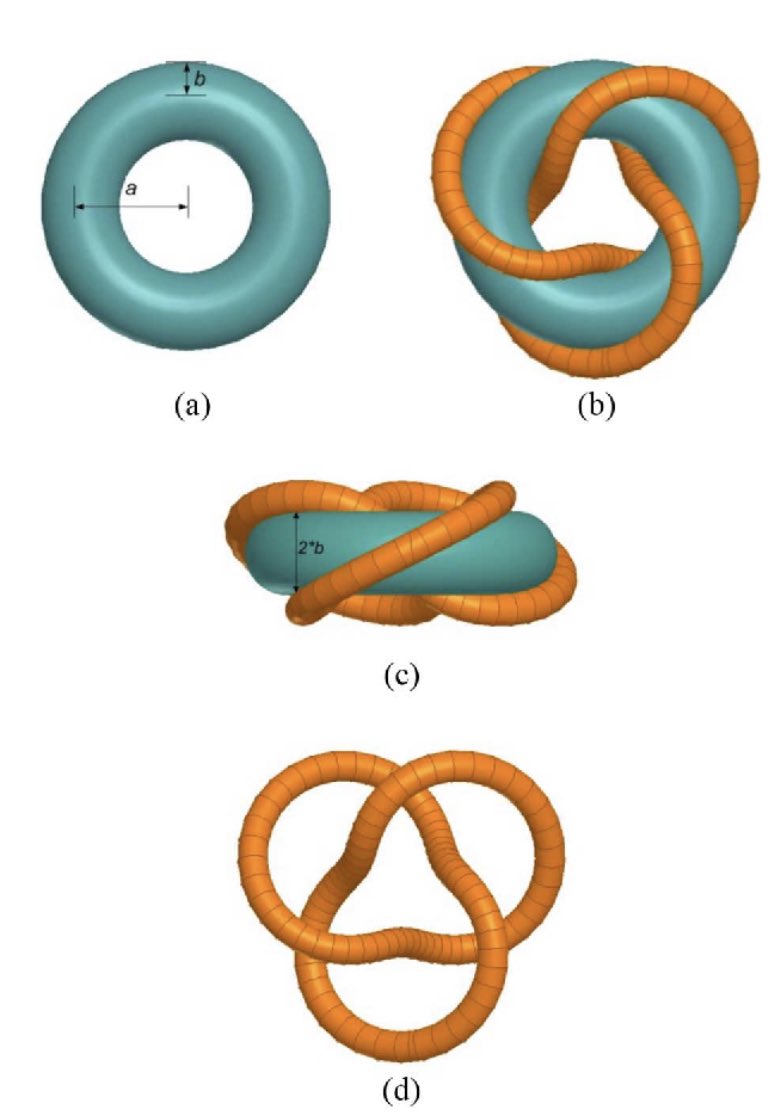
I was initially visualizing 3D volumes, but wanted a better view of the structure of the dependencies between the volumes. Got an idea to use a torus from the three utilities puzzle:
https://m.youtube.com/watch?v=VvCytJvd4H0

(2/4)">https://m.youtube.com/watch...

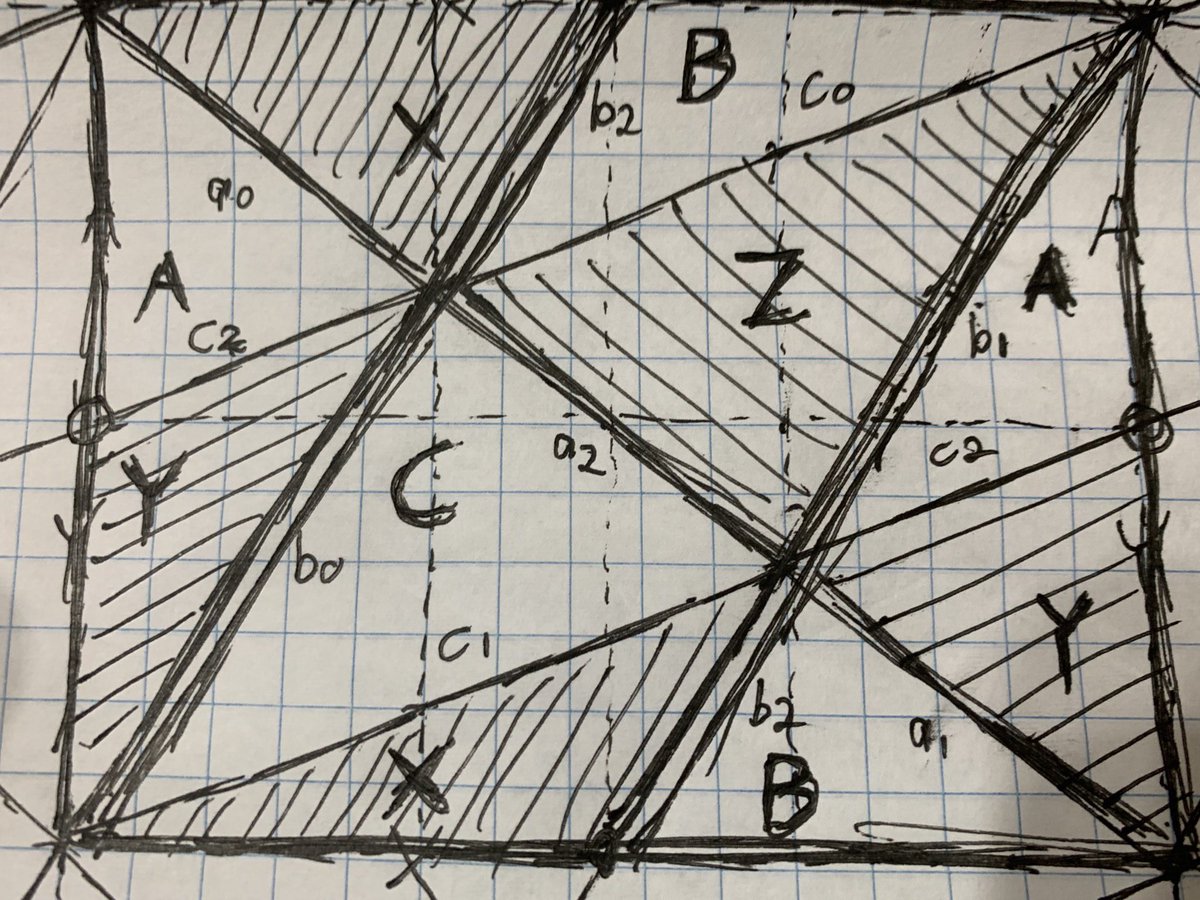
Mapping volumes to triangles and their common factors to edges yielded triangles that seamlessly wrapped around a torus. But to connect properly the strip had to wrap at a 3:2 ratio. In other words, the strip is bounded by a trefoil knot!

(3/4)

Went down this rabbit hole because I was hoping for a cheaper way to find times at which a linearly interpolated matrix has a determinant of zero. Have not improved on solving for roots of a cubic equation, but these connections seemed fun and maybe worth sharing anyway!

(4/4)

Gotta issue a retraction - the triangle strip is coiled like a spring, it doesn& #39;t actually form a knot. Got a little overeager and *maybe* saw fancier topology than was actually present :-/

I still think the 360 degree twist in the connectivity is potentially interesting though!

Oh here we go, much better than my little sketch. https://twitter.com/SxDXKLEEapigl92/status/1298593508496830464">https://twitter.com/SxDXKLEEa...