Very excited to share our newest paper
combining machine learning & physics. We develop normalizing flows that impose the elaborate of symmetry groups you find in fundamental particle physics.
It's a beautiful mix of math, ML, and physics
https://arxiv.org/abs/2008.05456 

It took several months to work through a series of challenges. Shout out to the team:
Denis Boyda, Gurtej Kanwar, @sracaniere, @DaniloJRezende,
@msalbergo, @kylecranmer, Daniel Hackett, Phiala Shanahan
https://arxiv.org/abs/2008.05456 

This extends our previous work & was much more involved. The goal as before is to dramatically speed up "lattice techniques", which is a powerful computational approach to studying fundamental physics. Here’s a twitter thread on our last paper: https://twitter.com/KyleCranmer/status/1239346481942986757?s=20

In this setting we are trying to model a quantum mechanical field in a discretized space-time lattice. Here's an example from Lattice Quantum Chromodynamics. This animation is just 1 sample from the 4D distribution (where time is used for 1 dimension). Think of a 4-d image.

We don't want just a single "image" (lattice configuration), we want to sample the high-dimensional distribution of configurations predicted by a fundamental theory. That distribution is intractable. Typically people use Hamiltonian Monte Carlo for this, but it has limitations.

Part of the trick is that the high dimensional configurations have many redundant directions related to what is called a Gauge Symmetry. Gauge symmetries are at the heart of quantum field theory. Thanks Emmy Noether!
https://en.wikipedia.org/wiki/Gauge_theory https://www.symmetrymagazine.org/article/june-2015/mathematician-to-know-emmy-noether

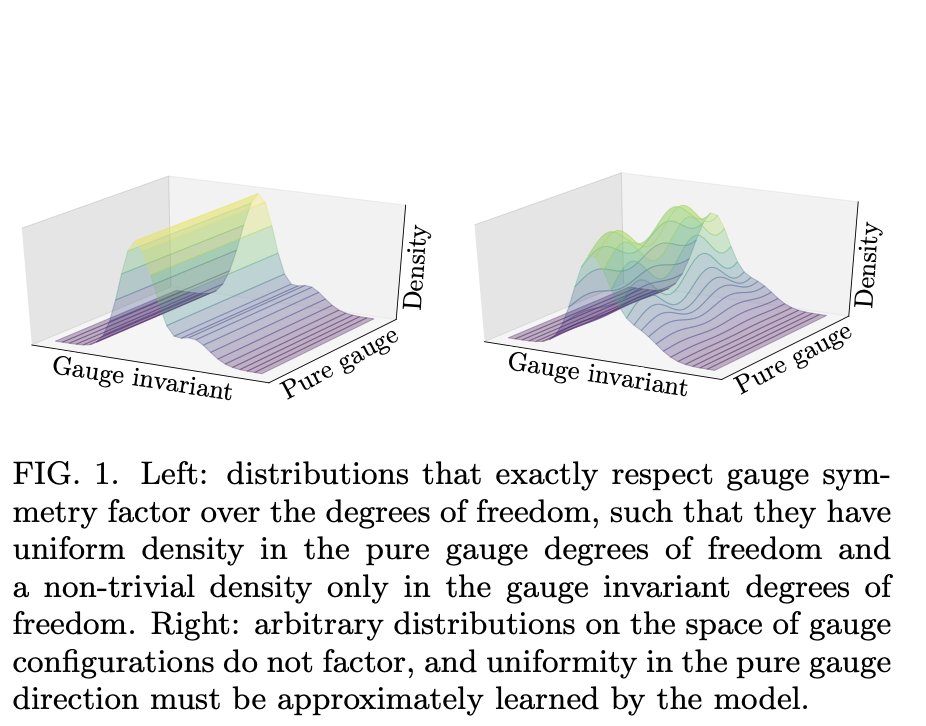
We can call those redundant degrees of freedom "pure gauge" degrees of freedom xΩ and the physically meaningful "gauge invariant" degrees of freedom x/Ω. Then we know the true distribution should factorize like this:
p(x/Ω, xΩ) = p(x/Ω)p(xΩ) = p(x/Ω) x const.

However, standard normalizing flows don't work well for this problem. With local gauge invariance, one can "rotate" at every site on the lattice. The symmetry group is huge!
So we want to build this into the network.

In our last paper we figured out how to do this with a simpler group called U(1) — the group of complex numbers of the form exp(iθ) — which is equivalent to a circle. https://twitter.com/KyleCranmer/status/1239351713095704576?s=20

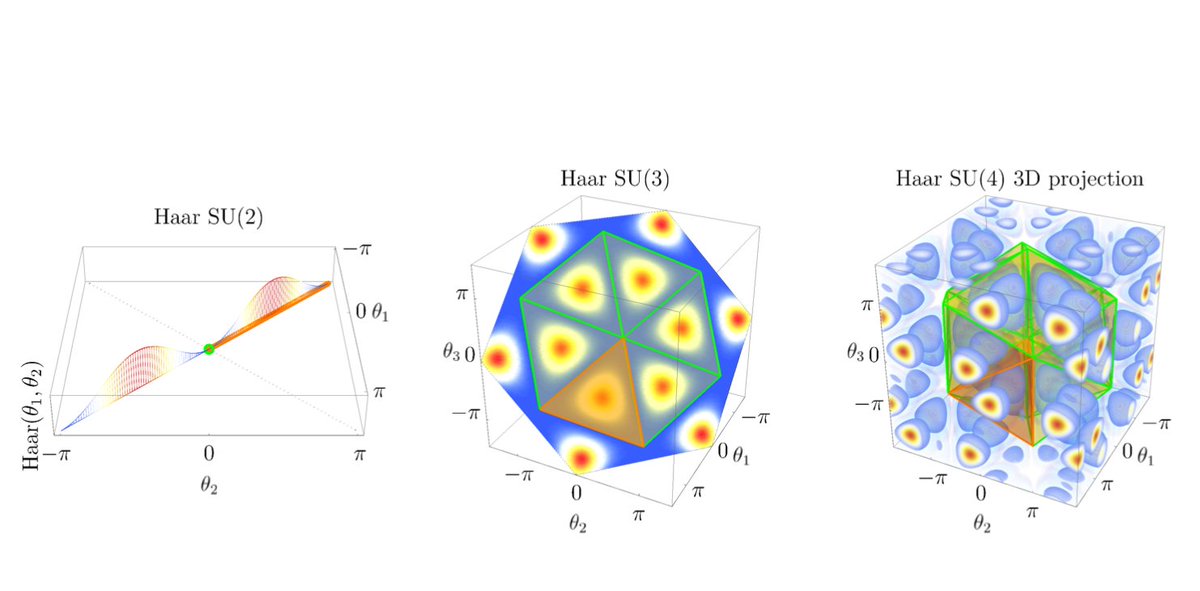
But to describe the weak and strong fundamental forces we need to be able to extend the idea to the Lie groups SU(2) and SU(3). This takes us into some beautiful group theory, which we have to realize in concrete numerical form that plays well with automatic differentiation

SU(N) is the name for the special unitary group of degree N — it is the group of NxN unitary matrices with determinant 1. @johncarlosbaez recently had a nice thread about its geometric manifestation https://twitter.com/johncarlosbaez/status/1287064691299119105?s=20

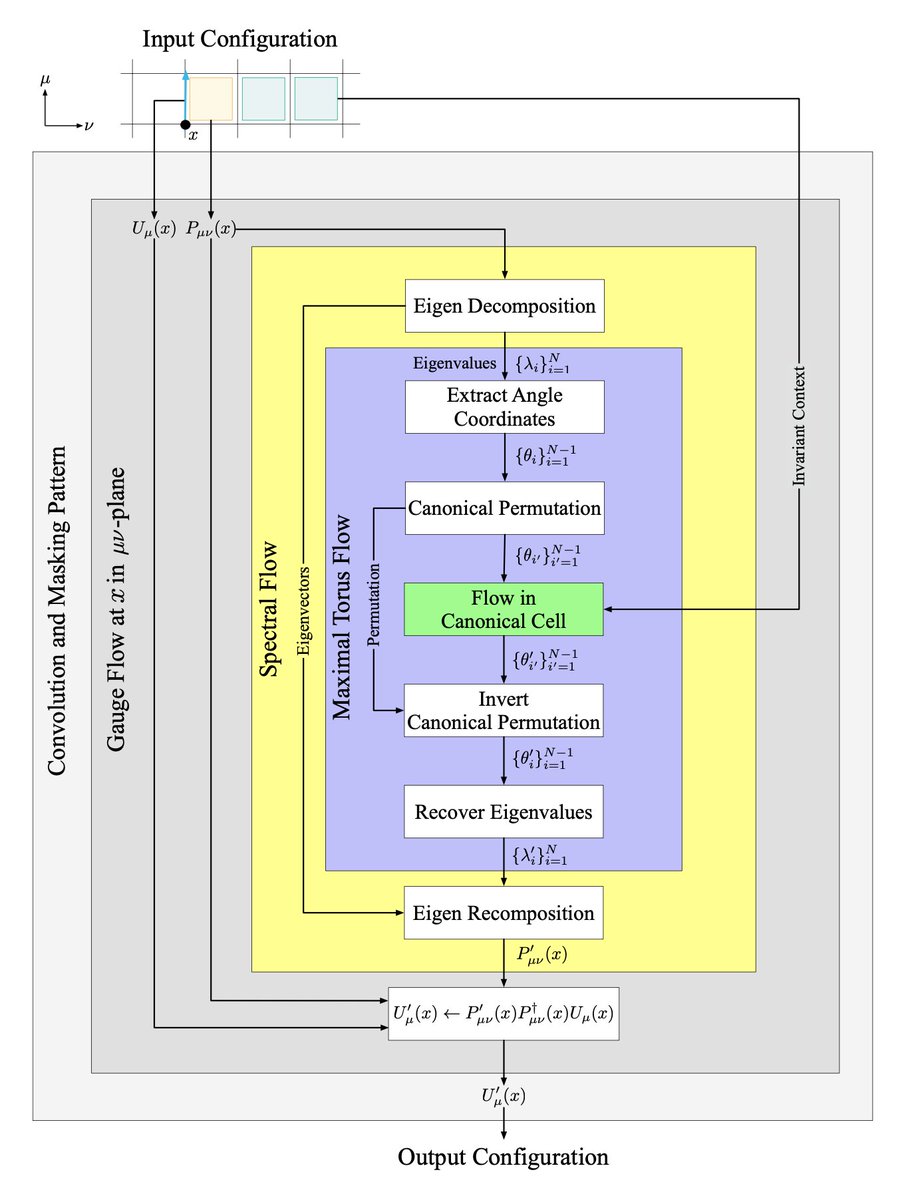
We do this by modeling elements of SU(N) in terms of their eigenvalues & location on the maximal torus. In addition to the nice smooth structure, there is also a discrete Weyl group, which is related to permutations of the eigenvalues. Respecting this discrete symmetry is harder

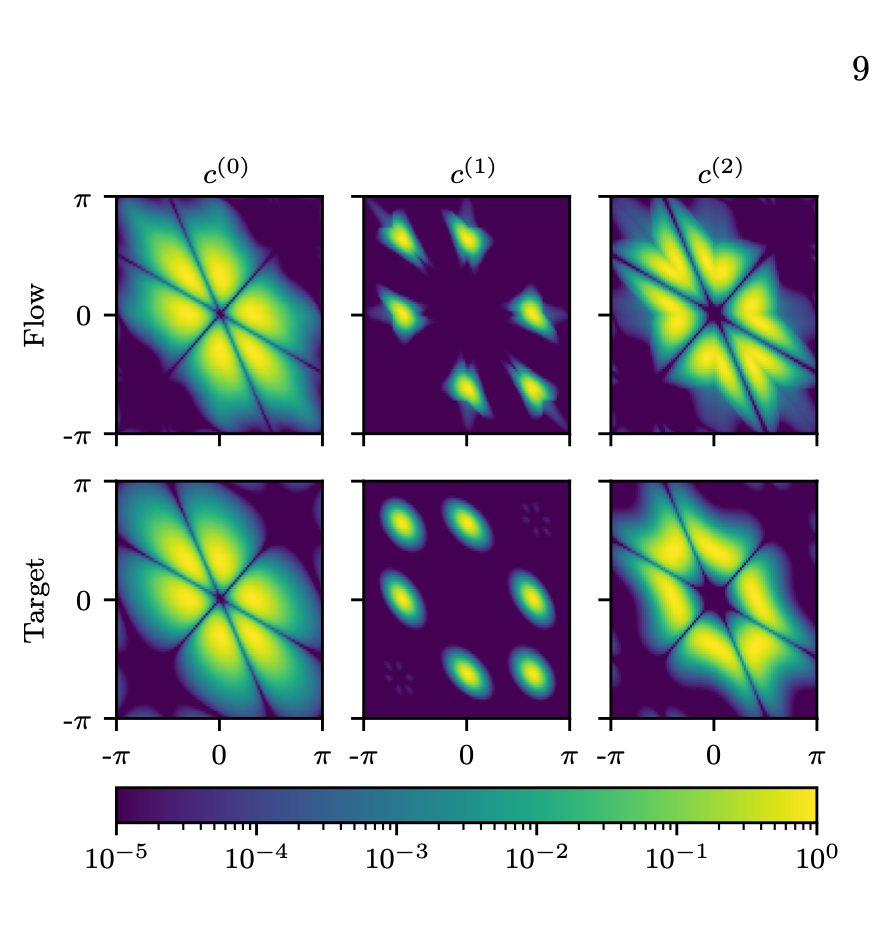
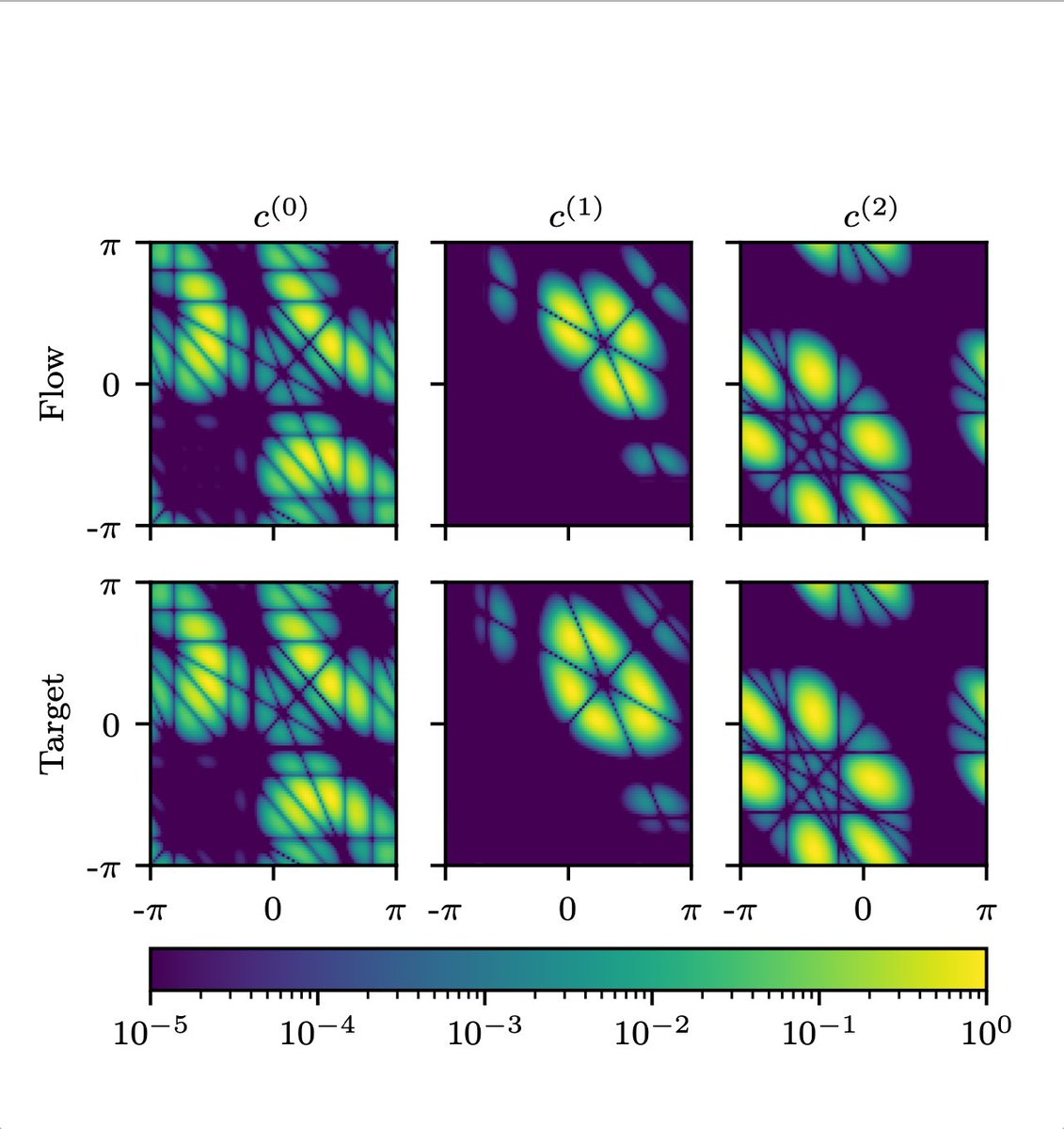
We developed an algorithm that works for any SU(N). Below is an image of a slice through the 8 dimensional torus that describes elements of SU(9). Lines of zero density correspond to locations where the slice crosses through walls of the cells (where density goes to zero).

I’ve learned a ton and really enjoyed this project. I’ve been blown away repeatedly by my collaborators intuition and ingenuity. The amazing Gurtej Kanwar will be talking about this today/tomorrow (Thursday, Aug 13) at 10AM Eastern Time:
http://ctp.lns.mit.edu/latticecolloq/ 

thank you for coming to my Ted talk.

And see the fantastic thread from @DaniloJRezende on the same paper
https://twitter.com/danilojrezende/status/1293738960737509376?s=21 https://twitter.com/danilojrezende/status/1293738960737509376