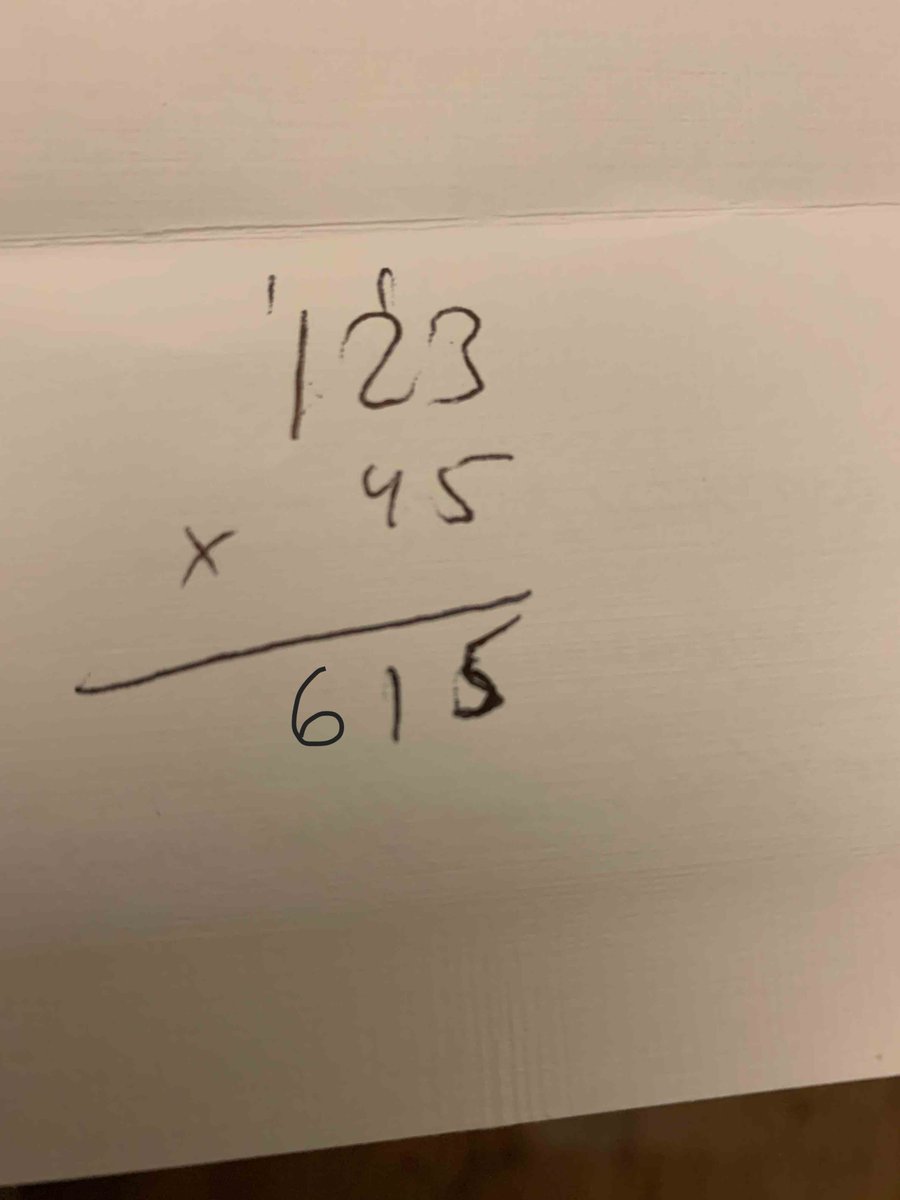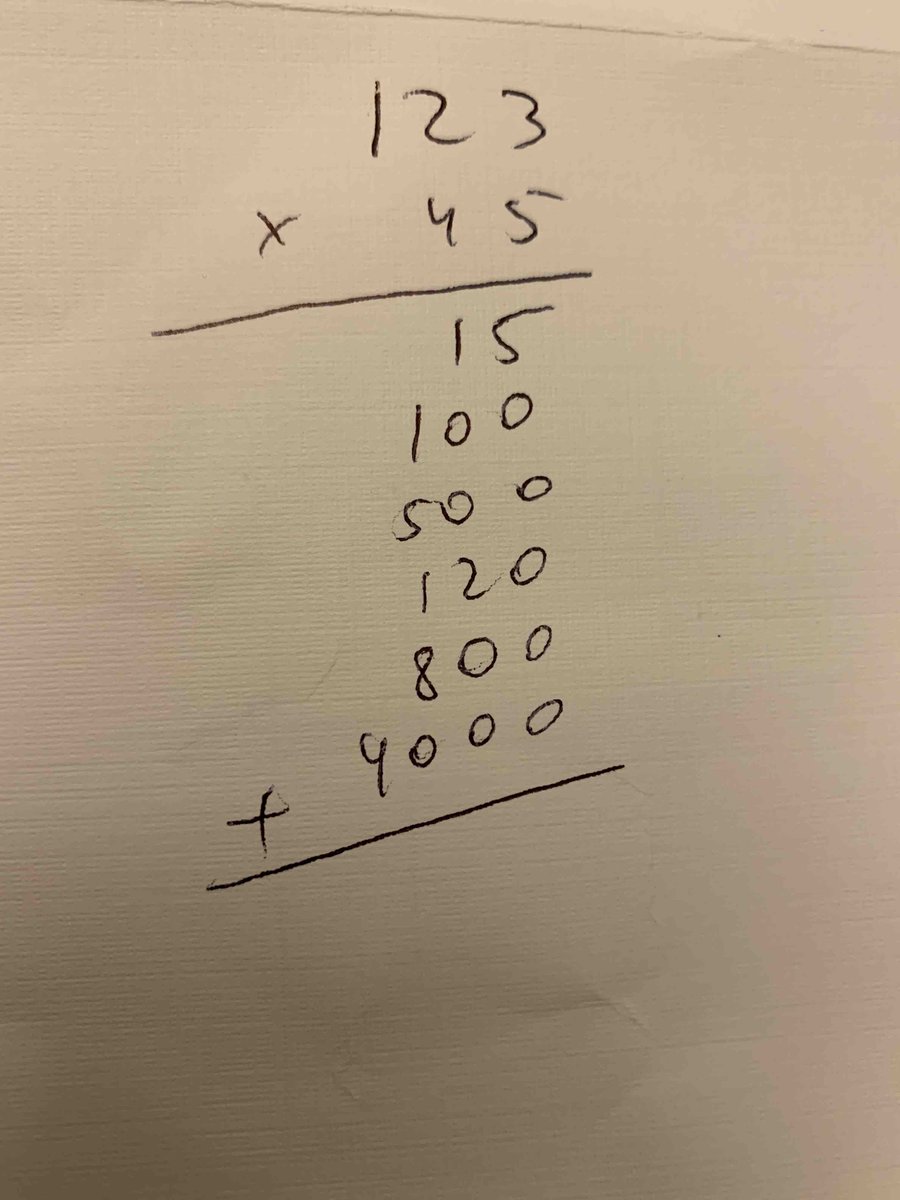Hey everybody! Gather round; I just discovered this incredible ancient way for multiplying! It& #39;s so simple; here& #39;s what you do: Say you want 3x4. So you make 3 horizontal lines, and 4 vertical lines, and count the intersections! I can& #39;t believe nobody ever showed me this!(cont& #39;d)
2/ Actually I& #39;m not just trolling, I do have a point. People keep getting excited by "new algorithms" like this because adults, while fully capable of executing the "standard" algorithm, actually have zero understanding of *why* it works. Let& #39;s look at it together:
3/ Say you& #39;re multiplying 123x45. So you do 5x3 = 15, write the 5 but carry the 1 (above the 2). Then 5x2=10 but remember to add the 1 (add? I thought we were multiplying?), so really 11; write the 1 and carry another 1. Finally, 5x1+1=6. So our first row is 615. What the hell?
Now imagine teaching this to a child learning it for the first time. It makes no sense (and the grownup doesn& #39;t know why either, but they& #39;ve been dutifully trained on it).
Then somebody comes along with a "Japanese" method, and we all get excited that we "finally understand".
Then somebody comes along with a "Japanese" method, and we all get excited that we "finally understand".
5/ So what *is* going on in the standard algorithm?
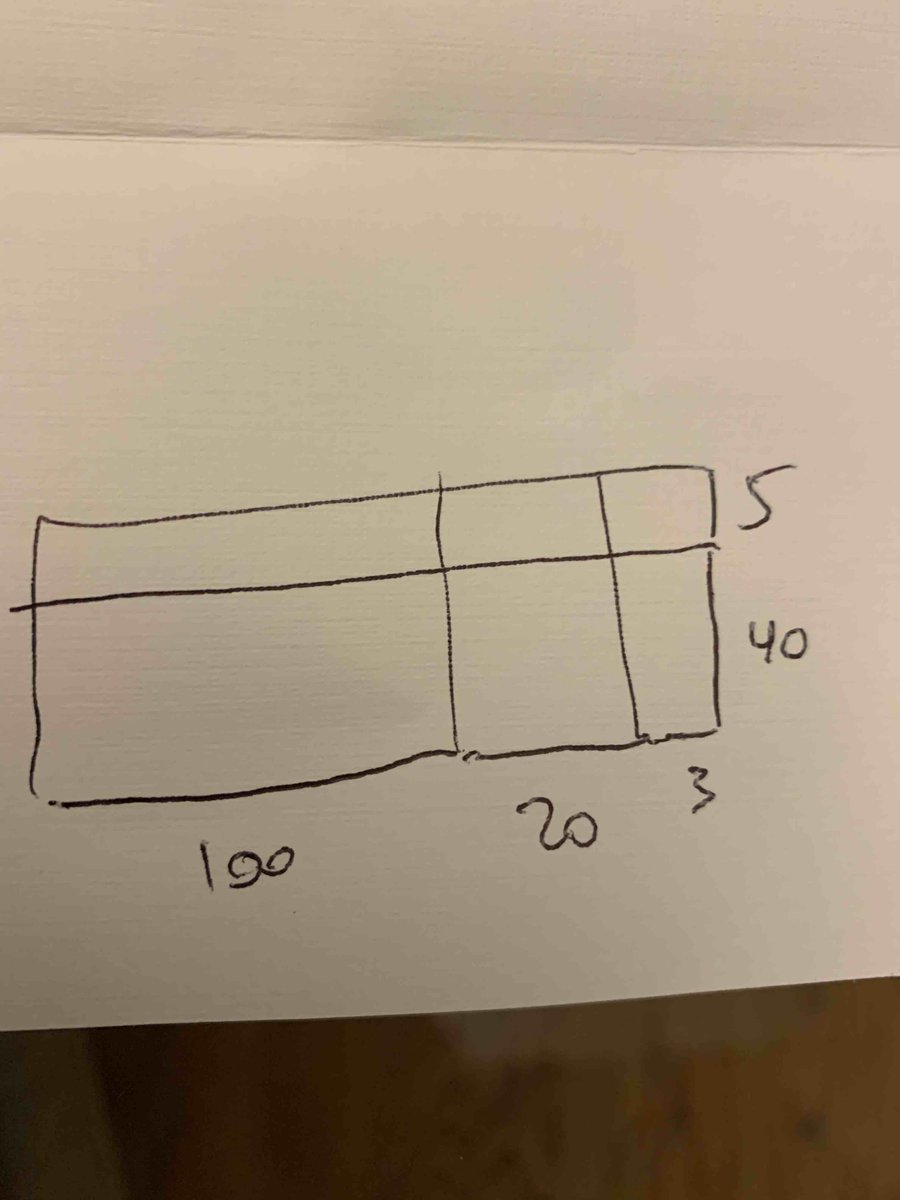
Remember: multiplication is all about rectangles! When you ask for 123x45, you want the area of a 123x45 rectangle. Since 123=100+20+3, you really want (100+20+3)x(40+5). Maybe you were taught something called "distribution"
Remember: multiplication is all about rectangles! When you ask for 123x45, you want the area of a 123x45 rectangle. Since 123=100+20+3, you really want (100+20+3)x(40+5). Maybe you were taught something called "distribution"
6/ but that was a long time ago. Just draw a picture, and all becomes obvious! Starting in the top right and going across, the little corner is 5x3=15, then 5x20=100, then 5x100=500; those three add up to 615. *That* is exactly what that first row means in the standard algorithm.
7/ The most "natural" way to track this is to just write all the products out and add (as shown). This is actually what I teach my own kids, not the standard.
Now, this gets a little tiresome, with all those zeros, so the standard algorithm compresses them to save space+time.
Now, this gets a little tiresome, with all those zeros, so the standard algorithm compresses them to save space+time.
8/ That compression was important when "calculator" meant a human; these days nobody does 8917x124 by hand. (That doesn& #39;t mean it& #39;s not important for people to understand what multiplication means or how to do it efficiently!)
Anyway, if you want to "test" some newfangled method
Anyway, if you want to "test" some newfangled method
9/ just give it some slightly larger numbers than the "cute", carefully chosen example they show you. I don& #39;t think anybody would be retweeting the "Japanese method" if it was illustrated on 78x93...
End of rant.
End of rant.

 Read on Twitter
Read on Twitter