A short thread about how infinitesimally small spaces (called non-reduced schemes) can appear in the real world. We can build them out of ball-and-socket joints and rigid rods. https://twitter.com/ChocoLinkage/status/1266326082061340672">https://twitter.com/ChocoLink... 1/n
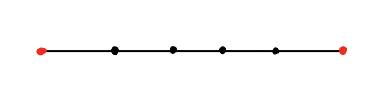
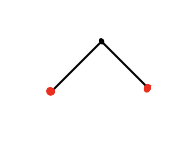
Here are the basic building blocks. The black and red dots are ball-and-socket joints, and the black line segment is free to spin around them, as long as its length remains the same. But the red dot is pinned to the page, while the black dot is free to move. 2/n
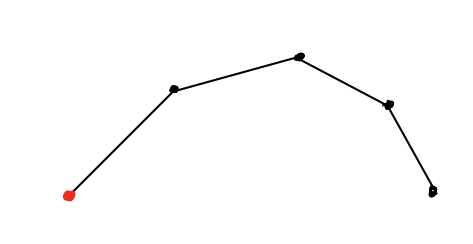
We’re allowed to connect the rods together at the black dots. These pictures are a kind of “cartoon model” of physical objects like the arm below. Let’s call them “linkages.” 3/n
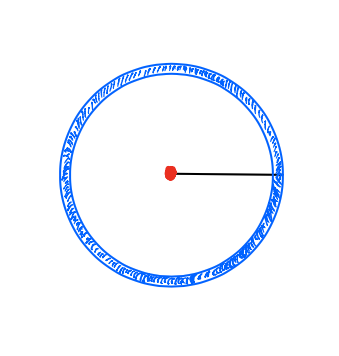
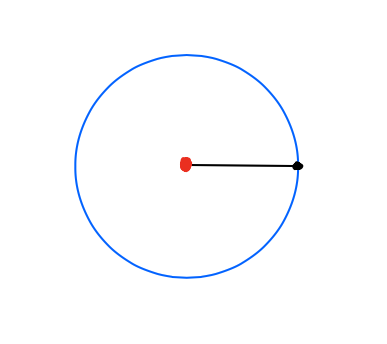
The kind of question I& #39;m interested in is: what are the possible configurations of these linkages? For example, if we just have one rod connected to a red joint, it can move in a circle. This circle is called its "configuration space." 4/n
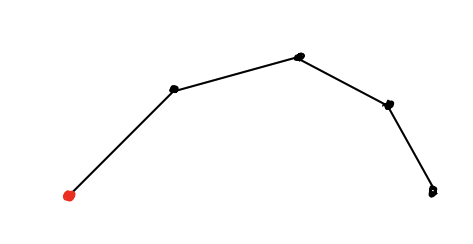
Of course more complicated linkages can have much more complicated configuration spaces; for example the linkage below has a 4-dimensional configuration space (one dimension for each joint). It& #39;s a space called 4-torus, a kind of 4-dimensional donut. 5/n
But I want to talk about linkages with the simplest possible configuration space -- rigid linkages. Their configuration spaces are zero-dimensional. 6/n
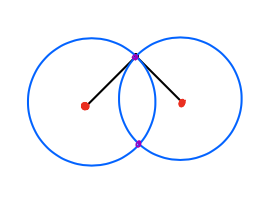
Here& #39;s an example. Suppose the two rods below have a length of one foot, and the two red dots are less than 2 feet apart. Then no matter how you jiggle the black dot, the configuration below will stay rigid. 7/n
In fact the configuration space — the set of possible positions of this configuration — is just two points: the purple dots in the picture below. These are where the circles swept out by the two rods intersect. 8/n
In equations, if the red dots are a distance of d feet apart, the configuration space is the set of solutions to the system of equations
x^2+y^2=1
(x-d)^2+y^2=1
9/n
x^2+y^2=1
(x-d)^2+y^2=1
9/n
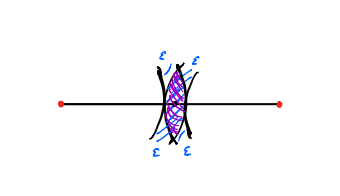
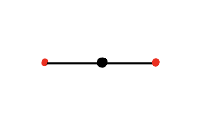
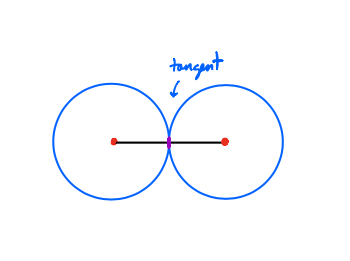
Now what if d is exactly 2, so the linkage looks like the picture below? Now the configuration space is just one point. But intuitively you’d think this linkage would be a bit wobbly, right? 10/n
This is because we’re now looking at the intersection of two tangent circles. So the configuration space should somehow remember that tangency. 11/n
The way to keep track of this is an old trick from algebraic geometry — instead of thinking about a space, we’ll think about polynomial functions on that space. 12/n
The set of all polynomial functions in two variables is ℝ[x,y]. To get the functions on our configuration space, we want to identify all polynomials which differ by something vanishing on the configuration space. 13/n
Now there are some obvious functions vanishing on our configuration space:
x^2+y^2-1 and (x-d)^2+y^2-1,
since these are precisely the functions which define it! 14/n
x^2+y^2-1 and (x-d)^2+y^2-1,
since these are precisely the functions which define it! 14/n
So the functions on our configuration space should be
ℝ[x,y]/(x^2+y^2-1, (x-d)^2+y^2-1). And a direct computation gives: (15/n)
ℝ[x,y]/(x^2+y^2-1, (x-d)^2+y^2-1). And a direct computation gives: (15/n)
What does this mean? Well ℝ^2 is the set of functions on two points, which is exactly our configuration space if d<2. ℝ[x]/x^2 is some mysterious gadget, which I claim encodes the fact that the circles are tangent if d=2. 16/n
And if d>2, the configuration space is empty! So the only functions on it are “imaginary.” 17/n
The mysterious “space” which has the property that functions on it form the ring ℝ[x]/x^2 is the kind of infinitesimally small space (a non-reduced scheme) I alluded to at the beginning of the thread. Note that x^2=0! 18/n
We can make even more wiggly linkages. For example, the string of several rods below will be more wiggly; its configuration space will be higher-dimensional as a real vector space. 19/n
OK, but what does this have to do with the real world? In real life rods aren’t actually perfectly rigid — they have a bit of give. So does this really have anything to do with real life? 20/n
Let’s try to make a more physically realistic model — let’s allow the rods to change length up to some small constant ε. So the configuration space of a single rod attached to a red joint is a “ring,” as below. 21/n
This ring — or annulus — has width ε. Now let’s look at what happens with our rigid configurations from before. 22/n
If the red dots are less than 2 feet apart, the configuration space will be the intersection of two annuli. It will look like two copies of the purple region below. 23/n
If the red dots are exactly 2 feet apart, the configuration space will look like the intersection of two “tangent” annuli — the purple region below. 24/n
And if they’re more than 2 feet apart, the configuration space will still be empty as long as ε is small enough 25/n
Now here’s the cool bit. Let’s look at the areas of these regions as ε tends to zero. I claim that the rate at which these areas tends to zero reflects the nature of our original configuration spaces! 26/n
In particular, if the configurations spaces were non-reduced, the areas will tend to zero more slowly. So in fact, even this real-life situation knows something about our idealized infinitesimally small spaces. 27/n
There’s a lot more known about linkages. For example, you might ask which shapes can arise as configuration spaces of linkages. Final cool fact: Kapovich and Millson show that basically any algebraic shape can arise: https://www.math.ucdavis.edu/~kapovich/EPR/KM_2002.pdf
28/n">https://www.math.ucdavis.edu/~kapovich...
28/n">https://www.math.ucdavis.edu/~kapovich...
FIN 29/n, n=29

 Read on Twitter
Read on Twitter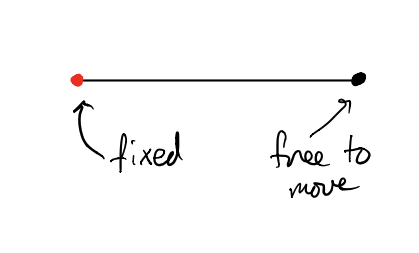


![So the functions on our configuration space should be ℝ[x,y]/(x^2+y^2-1, (x-d)^2+y^2-1). And a direct computation gives: (15/n) So the functions on our configuration space should be ℝ[x,y]/(x^2+y^2-1, (x-d)^2+y^2-1). And a direct computation gives: (15/n)](https://pbs.twimg.com/media/EesQW07WsAAnBP4.png)