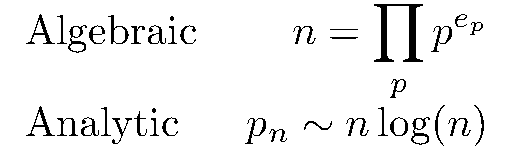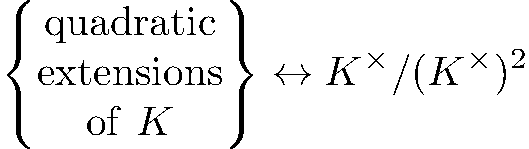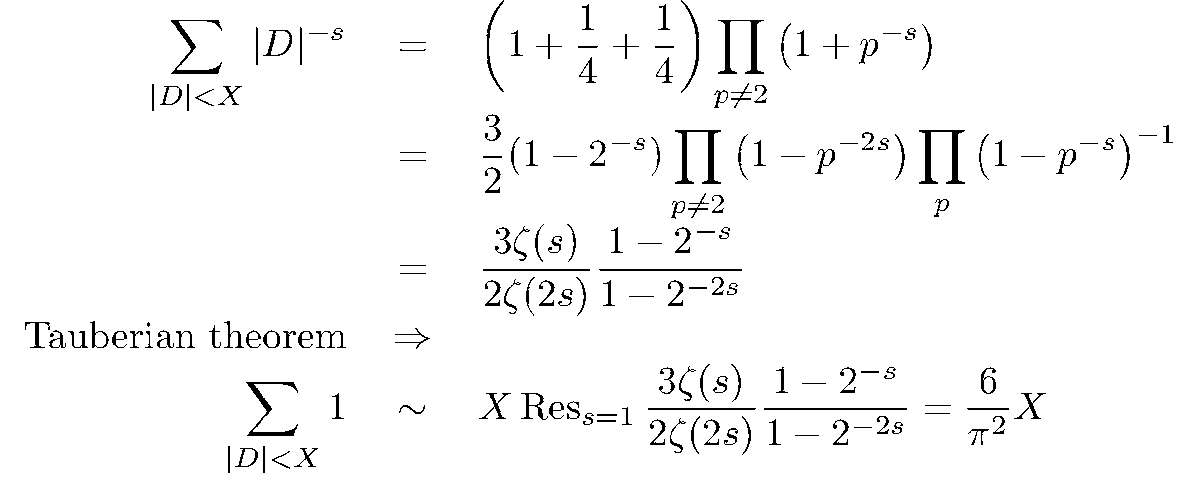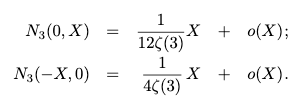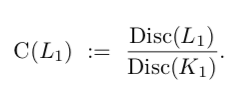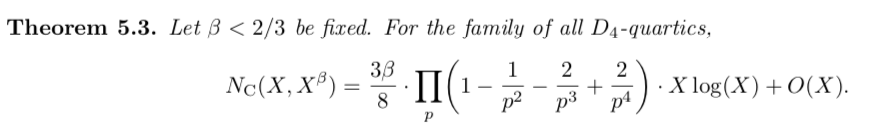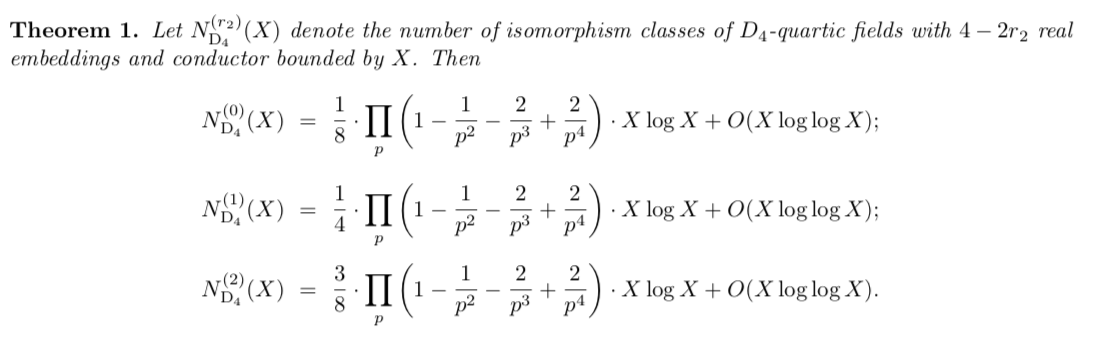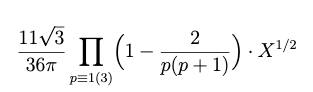Just finished responding to a great referee report. As per tradition, a twitter thread! Warning: This one is about pure mathematics and is a bit long. https://arxiv.org/abs/1704.01729 

Some background. Number theory is often described as the study of the integers and things that look a lot like them. Interesting questions tend to be either "algebraic" facts about individual objects and "analytic" facts about families of objects.

As an example, an algebraic fact might be that there is a unique way to write every integer as a product of primes. An analytic fact is that nth prime has magnitude around n * log(n).

Another interesting example is finite field extensions of the rational numbers. A big open algebraic question about these objects is whether every group arises as a Galois group of such an extension (the inverse Galois problem) https://en.wikipedia.org/wiki/Inverse_Galois_problem

If we focus on extensions of a fixed degree, we can sometimes describe all extensions that have a fixed Galois group. For instance, quadratic extensions of ℚ all look like ℚ(√D) for D ∈ Z where D is the discriminant

It turns out that the only possible discriminants D of a quadratic field are squarefree D ≡ 1 (mod 4) and D = 4m where m ≡ 2, 3 (mod 4) is squarefree. The more general version of this result is called "Kummer theory".

From this algebraic fact, we can answer an analytic question: How many quadratic fields are there with discriminant at most X? With this explicit characterization, it's a pretty easy computation!

Well, if we can write down all quadratic fields, can we do cubic fields? It turns out that the answer is yes, and the answer, while beautiful, is a bit more complicated....

The algebraic fact that is used is called the Delone-Fadeev correspondence. It associates to a binary cubic form a cubic field, and shows any two binary cubic forms that yield the same field are GL_2(ℚ) equivalent

It turns out that this is actually true *over the integers* as well! To every binary cubic form with integral coefficients, we can associate a free ring of rank 3 over ℤ and forms yield the same ring iff they are GL_2(ℤ) equivalent

Using this correspondence over the integers, we can now answer the analytic question: How many cubic fields are there with discriminant at most X? Indeed, we can get a very precise estimate of this value! https://arxiv.org/abs/1005.0672 

How do we do this? The process has three steps: 1) Every number field of degree d has a distinguished rank d ring: its ring of integers. 2) Counting integer points in uniformly growing shapes is easy. 3) We can pick out rings of integers through series of congruence conditions.

This general framework, whose components are typically called "the geometry of numbers" (2) and "sieving" (3) was introduced to this class of problems by Davenport and Heilbronn in the 1950s.

Today this 1-2-3 is most associated with my advisor, Manjul Bhargava, who used it to great effect to count quartic and quintic extensions of fields and show facts like "the average rank of elliptic curves is bounded" https://arxiv.org/abs/1006.1002 

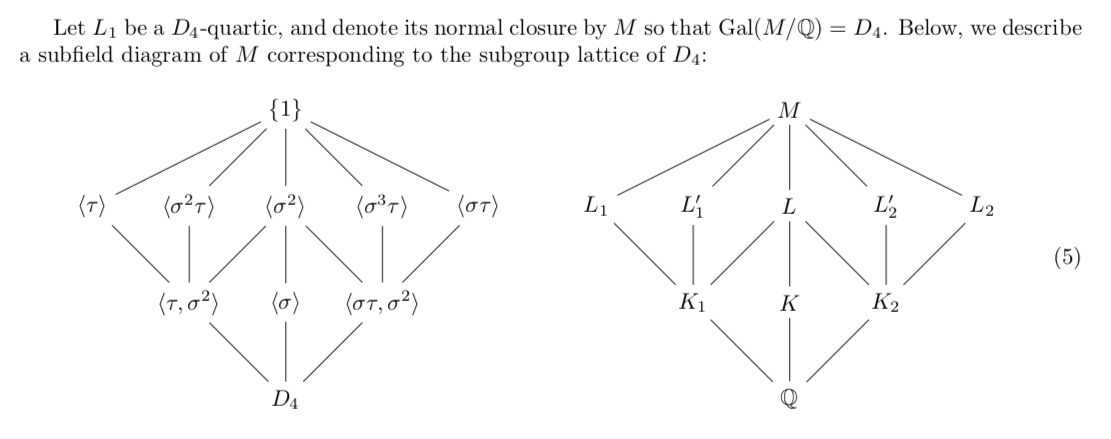
Enough history. What did we do? We get a bit more specific and begin by asking "How many quartic fields have Galois group D₄ and have discriminant < X?" This was actually answered by Cohen, Diaz y Diaz, and Olivier in 2003: https://www.cambridge.org/core/services/aop-cambridge-core/content/view/4FAECFC2E214F43D49191EE75ADCD780/S0010437X02000520a.pdf/enumerating_quartic_dihedral_extensions_of_open_q.pdf

How did they do it? D₄ fields are very special. If you look at the group structure of D₄, you'll notice that every quartic field that has Galois group D₄ must have a quadratic subfield! CDO thus count quad exts of quad exts

But you can see something strange above: There's no (known) Euler product for the constant in the count of D₄ fields by disc. This bothered a lot of us because previous heuristics indicated there should be one. Indeed, this one:

Sadly, CDO's c(D₄)≈0.052, whereas the heuristic is ≈0.406. But what if we changed the invariant we counted by? Instead of the discriminant, are there other interesting invariants of fields? Of course!

Discriminants of fields are actually a special case of something called an Artin conductor. These all arise from representations of the Galois group of the (Galois closure of the) field. https://en.wikipedia.org/wiki/Artin_conductor

The discriminant arises from the "permutation representation" Gal(K/ℚ) -> GL_n(ℚ-bar) where the action is on Hom(K, ℚ-bar), the [K:ℚ]-dimensional vector space of embeddings of K into its algebraic closure.

(If you've never seen this before, this is just a very fancy but very useful way of restating the fundamental theorem of Galois theory.)

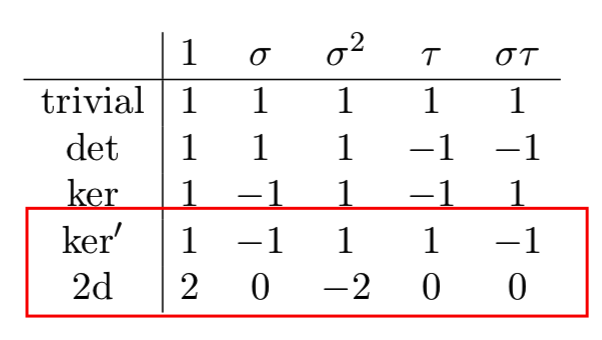
Now the permutation representation always contains a one-dimensional trivial representation, so usually we quotient by this to get the "standard representation" of Gal(K/ℚ) ≤ Sym([K:ℚ]). The Artin conductor of this repn is disc(K/ℚ)

If Gal(K/ℚ) = Sym(n), this representation is irreducible... but not if Gal(K/ℚ) = D₄! Indeed, it splits into D₄'s two-dimensional irrep and a one-dimensional irrep highlighted below. What if we count D₄ fields by 2d's conductor?

You can actually get pretty far with the methods in CDO! Indeed, CDO exploits the relative discriminant formula to compute the discrimimant of L₁. The Artin conductor turns out to drop a factor of disc(K₁)

But we can't quite get there. These methods only allow us to count as long as disc(K₁) is not too large relative to disc(L₁), indeed, only until disc(K₁) << disc(L₁)^{2/3}.

We got stuck here for a couple years, until we noticed D₄ has an outer automorphism! That is, the pair of D₄ fields (L₁, L₂) are canonically related. And it turns out that disc(K₁) > disc(L₁)^{1/2} => disc(K₂) < disc(L₂)^{1/2}!

For the rest of the paper, we combine some analytic techniques with the 1-2-3 of geometry of numbers, relying on some of Melanie Wood's previous work. The result? An Euler product!

So why do we get an Euler product, but CDO do not? Is it reducibility of the representation? No, because the count of C₃ extensions of ℚ by discriminant has an Euler product but C₃ only has one-dimensional irreps

One thing we don't quite conjecture is that the issue is that the 1d representation ker' of D₄ is not faithful. A consequence of this is that there are an infinite number of D₄ fields with cond(ker') bounded by X

Indeed, the Artin conductor of ker' is disc(K₁), and since K₁ has an infinite number of quadratic extensions, asking "how many D₄ fields with disc(K₁) < X" is not very interesting.

And that's a wrap on that paper. Come by next time for more research on policing and data science! ;-)