Today, we’re going to play a game I’m calling “IT’S JUST A LINEAR MODEL” (IJALM).
It works like this: I name a model for a quantitative response Y, and then you guess whether or not IJALM.
1/
It works like this: I name a model for a quantitative response Y, and then you guess whether or not IJALM.
1/
I’ll go first:
Y= \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \epsilon
You guessed it …. IJALM!
2/
Y= \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \epsilon
You guessed it …. IJALM!
2/
How about the lasso? Ridge regression?
IJALM but you’re not fitting it using least squares — it’s penalized/regularized least squares instead.
3/
IJALM but you’re not fitting it using least squares — it’s penalized/regularized least squares instead.
3/
How about forward or backward stepwise regression regression?
IJALM using a subset of the predictors. We fit the linear model using least squares on a subset of the predictors, though of course this isn’t the same is if we had performed least squares on ALL the predictors.
4/
IJALM using a subset of the predictors. We fit the linear model using least squares on a subset of the predictors, though of course this isn’t the same is if we had performed least squares on ALL the predictors.
4/
How about a piecewise constant model? Like this one?
You guessed it… IJALM, using basis functions that are piecewise constant. Typically fit with least squares.
5/
You guessed it… IJALM, using basis functions that are piecewise constant. Typically fit with least squares.
5/
What if it’s piecewise cubic?
Yes, IJALM, but now the basis functions are piecewise cubic. Fit with least squares.
6/
Yes, IJALM, but now the basis functions are piecewise cubic. Fit with least squares.
6/
Now, what if I predict Y using very complicated functions of my features, like e^{X_1}, \sin(X_2 X_3), and X_4^{17}?
Can’t fool me!!! IJALM! It’s linear in transformations of the features, e^{X_1}, \sin (X_2 X_3), and X_4^17. Can fit with least squares.
7/
Can’t fool me!!! IJALM! It’s linear in transformations of the features, e^{X_1}, \sin (X_2 X_3), and X_4^17. Can fit with least squares.
7/
OK, how about a B-spline (or regression spline)? [Remember: a kth-order B-spline is a piecewise kth-order polynomial w/derivatives that are cont. up to order k-1.]
You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares.
8/
You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares.
8/
Alright, on to the good stuff.
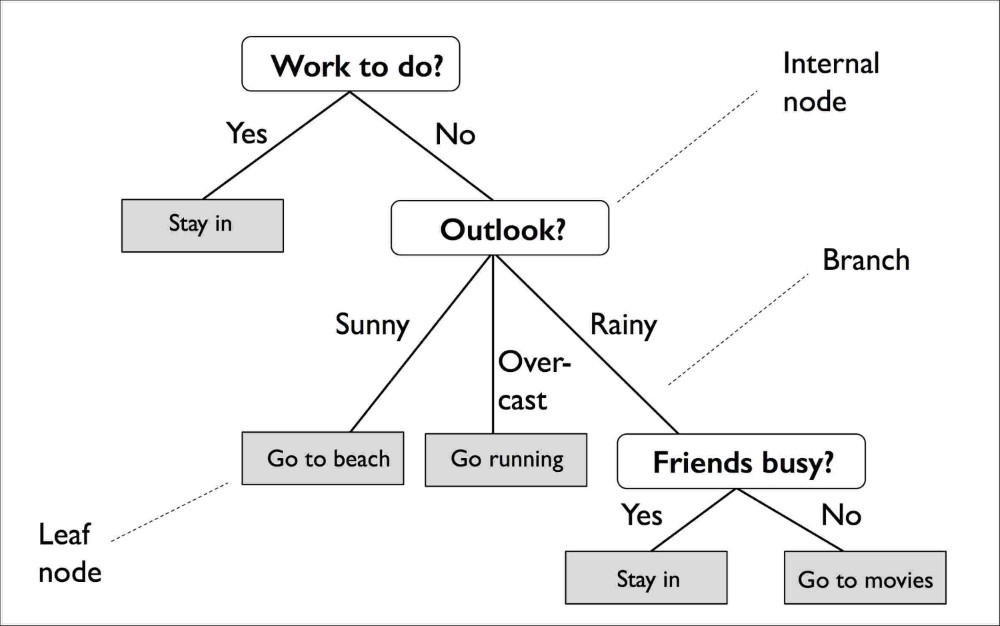
How about a regression tree? That is fundamentally non-linear, right?
Well, sort of . . . but no. IJALM w/ adaptive choice of predictors (predictors are indicator variables corresponding to a region of tree). Fit w/least squares.
9/
How about a regression tree? That is fundamentally non-linear, right?
Well, sort of . . . but no. IJALM w/ adaptive choice of predictors (predictors are indicator variables corresponding to a region of tree). Fit w/least squares.
9/
OK, this is getting old. How about principal components regression? Non-linear, right?
Well, no. The model is linear in the PCs, which are linear in the features, so, IJALM. Fit w/least squares.
Partial least squares? IJALM, for the same reason. Fit using least squares.
10/
Well, no. The model is linear in the PCs, which are linear in the features, so, IJALM. Fit w/least squares.
Partial least squares? IJALM, for the same reason. Fit using least squares.
10/
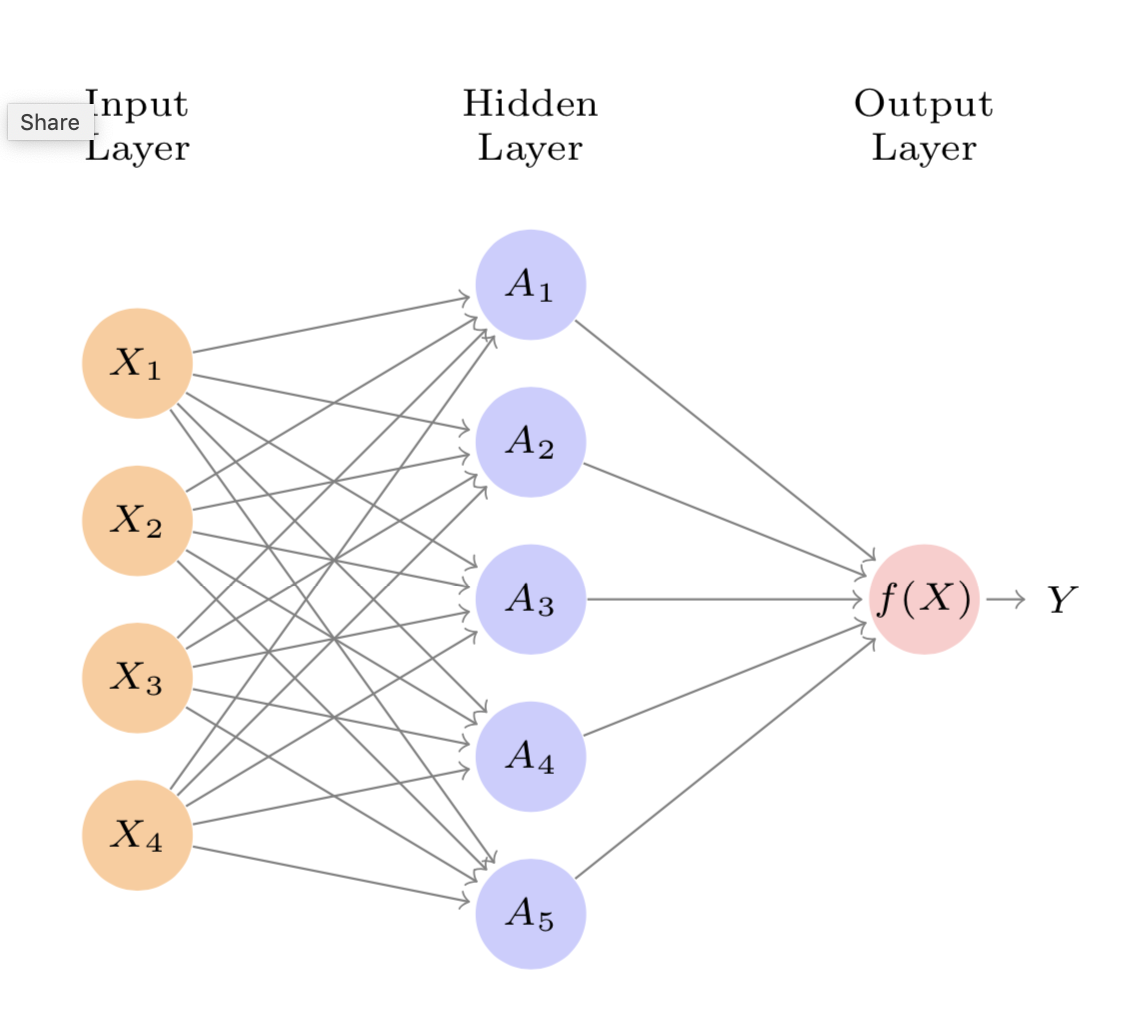
How about deep learning? Super non-linear, right?
Well, as a function of some non-linear activations, it& #39;s IJALM.
You can put lipstick on a linear model, but it’s still a linear model.
Fit it w/least squares … w/ bells & whistles like dropout, SGD, & regularization.
11/
Well, as a function of some non-linear activations, it& #39;s IJALM.
You can put lipstick on a linear model, but it’s still a linear model.
Fit it w/least squares … w/ bells & whistles like dropout, SGD, & regularization.
11/
So to sum it all up:
No you didn& #39;t fit a "super complicated non-linear model”. I bet you all my winnings from this round of IJALM it was actually JALM.
Perhaps not linear in the original features, and perhaps fit using a variant of least squares. But, IJALM nonetheless.
12/
No you didn& #39;t fit a "super complicated non-linear model”. I bet you all my winnings from this round of IJALM it was actually JALM.
Perhaps not linear in the original features, and perhaps fit using a variant of least squares. But, IJALM nonetheless.
12/
Linear models.
They might not be what your data thinks it wants, but they’re what your data needs, and they’re almost certainly what your data is going to get.
13/
They might not be what your data thinks it wants, but they’re what your data needs, and they’re almost certainly what your data is going to get.
13/
Thanks for playing!!!
Stay tuned for my next installment: IT’S JUST LOGISTIC REGRESSION (IJLR), which is literally just this same exact thread but now Y is a binary response.
14/14
Stay tuned for my next installment: IT’S JUST LOGISTIC REGRESSION (IJLR), which is literally just this same exact thread but now Y is a binary response.
14/14

 Read on Twitter
Read on Twitter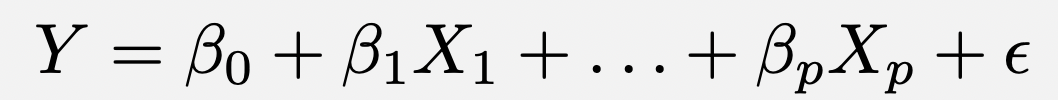
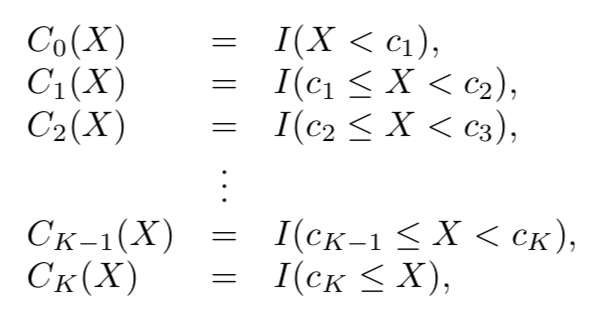
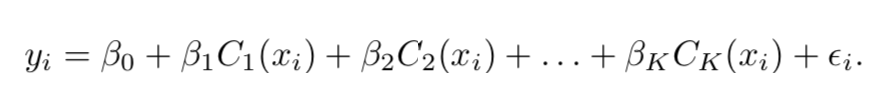
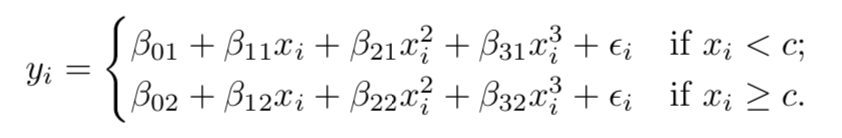
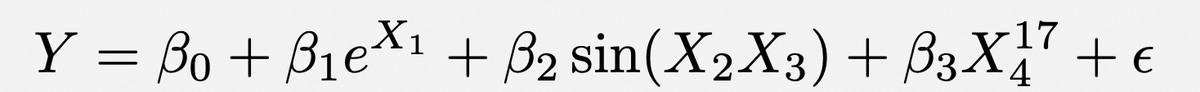
![OK, how about a B-spline (or regression spline)? [Remember: a kth-order B-spline is a piecewise kth-order polynomial w/derivatives that are cont. up to order k-1.] You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares. 8/ OK, how about a B-spline (or regression spline)? [Remember: a kth-order B-spline is a piecewise kth-order polynomial w/derivatives that are cont. up to order k-1.] You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares. 8/](https://pbs.twimg.com/media/EdpLw1tU0AAyWKS.png)
![OK, how about a B-spline (or regression spline)? [Remember: a kth-order B-spline is a piecewise kth-order polynomial w/derivatives that are cont. up to order k-1.] You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares. 8/ OK, how about a B-spline (or regression spline)? [Remember: a kth-order B-spline is a piecewise kth-order polynomial w/derivatives that are cont. up to order k-1.] You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares. 8/](https://pbs.twimg.com/media/EdpLyVOU4AAhlO8.png)