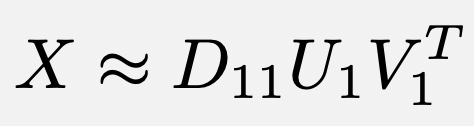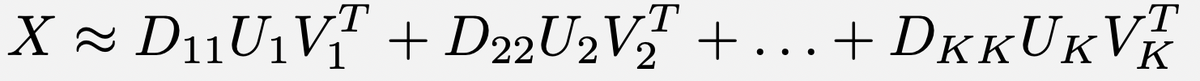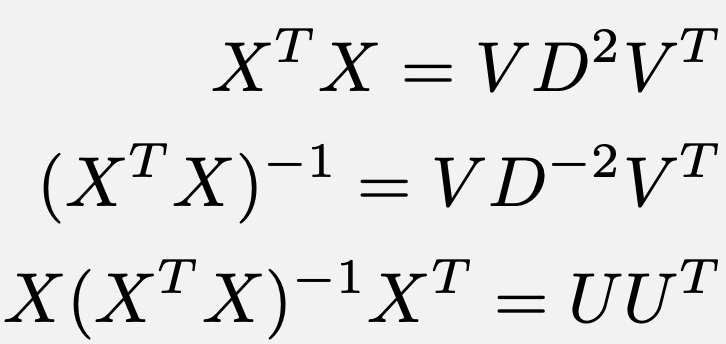So yesterday I asked you all what you wanted to hear about from me this week, and one answer stood out from all the others: the SINGULAR VALUE DECOMPOSITION (SVD).
https://twitter.com/genomixgmailcom/status/1285212264614768642?s=20
1/">https://twitter.com/genomixgm...
https://twitter.com/genomixgmailcom/status/1285212264614768642?s=20
1/">https://twitter.com/genomixgm...
The person who posted this tweet may or may not have known that in my normal life, while not curating the @WomenInStat account, I’m stanning hard for this matrix decomposition.
https://twitter.com/daniela_witten/status/1279915517654888448?s=20
2/">https://twitter.com/daniela_w...
https://twitter.com/daniela_witten/status/1279915517654888448?s=20
2/">https://twitter.com/daniela_w...
TBH asking to hear about SVD caught me a bit off guard, because the SVD is *not* usually considered to be a “women’s issue”.
3/
3/
But, many issues -- access to healthcare, re-opening schools, police brutality, etc. -- affect all people, but affect marginalized groups the most. And women (esp. Black, Indigenous, Women of Color, LGBTQ+) are a marginalized group in statistics.
4/
4/
So, by that logic, I guess now is as good a time as any for some real talk about the SVD.
5/
5/
So a lot of people think of the SVD as “just another matrix decomposition”.
But today I will argue that if you are in statistics or data science, it is the #1 matrix decomposition, and likely the only one you will ever need.
And believe me: you are going to need it.
6/
But today I will argue that if you are in statistics or data science, it is the #1 matrix decomposition, and likely the only one you will ever need.
And believe me: you are going to need it.
6/
First of all, what does the SVD do? You give me an $n \times p$ matrix $X$, and I’ll give you back 3 matrices $U$, $D$, $V$. Without loss of generality let’s assume that $n \geq p$. Then $U$ is an $n \times p$ matrix, and $D$ and $V$ have dimension $p \times p$.
7/
7/
$U$, $D$, $V$ “decompose” the matrix $X$ because $X=UDV^T$. Simple as that. But, what makes this decomposition special (and unique) is the particular set of properties of $U$, $D$, and $V$.
8/
8/
To begin, $U$ and $V$ are orthogonal matrices, which means that $U^T U = I$ and $V^T V = I$. (Also, if you’re keeping score at home, $V V^T = I$ as well. Don’t be fooled tho: $U U^T \neq I$ !!!!!!!)
9/
9/
In layperson’s terms, the columns of $U$ and $V$ are special: the squared elements of each column of $U$ and $V$ sums to 1, and also the inner product (dot product) btw each pair of columns in $U$ equals 0. And the inner product between each pair of columns of $V$ equals 0.
10/
10/
And $D$ is diagonal with nonnegative and decreasing elements: $D_{11} \geq D_{22} \geq \ldots \geq D_{pp} \geq 0$.
11/
11/
Some terminology: the diagonal elements of D are the SINGULAR VALUES, and the columns of U and V are the LEFT and RIGHT SINGULAR VECTORS.
12/
12/
First of all, let’s marvel that this decomposition is not only possible, but easily computable, & even unique (up to sign flips of columns of U & V). Like, why on earth should *every matrix X* be decomposable in this way?
Magic, that’s why.
13/
Magic, that’s why.
13/
OK, so, its existence is magic.
But, is it also useful? Well, YES.
14/
But, is it also useful? Well, YES.
14/
Suppose you want to approximate X w/a pair of vectors: that is, a rank-1 approx. Well, the world’s best rank-1 approximation to X, in terms of residual sum of squares, is given by the first columns of U & V:
$X \approx D_{11} U_1 V_1^T$ is literally the best you can do!!
15/
$X \approx D_{11} U_1 V_1^T$ is literally the best you can do!!
15/
OK, but what if you want to approximate X using two pairs of vectors (a rank-2 approximation)?
Just calculate
$X \approx D_{11} U_1 V_1^T + D_{22} U_2 V_2^T$
and call it a day.
16/
Just calculate
$X \approx D_{11} U_1 V_1^T + D_{22} U_2 V_2^T$
and call it a day.
16/
Want an even better approximation, using rank-K? You LITERALLY CAN’T BEAT THIS ONE
$X \approx D_{11} U_1 V_1^T + D_{22} U_2 V_2^T + \ldots + D_{KK} U_K V_K^T$
SO PLEASE DON’T BOTHER TRYING.
17/
$X \approx D_{11} U_1 V_1^T + D_{22} U_2 V_2^T + \ldots + D_{KK} U_K V_K^T$
SO PLEASE DON’T BOTHER TRYING.
17/
OK, so, the SVD gives me the best possible way to approximate any matrix. What is this good for??!!
18/
18/
Ever heard of principal components analysis (PCA)? This is just the SVD (after centering columns of X to have mean 0). Columns of V are PC loading vectors. Columns of U (up to scaling) are PC score vectors.
Bam!!!
19/
Bam!!!
19/
How about if you want to impute missing values in your data matrix X?
Assuming that the elements of X are randomly missing (rather than, for instance, larger elements more likely to be missing), the SVD gives you an effective and easy way to impute those values!!
20/
Assuming that the elements of X are randomly missing (rather than, for instance, larger elements more likely to be missing), the SVD gives you an effective and easy way to impute those values!!
20/
First, fill in missing elements using (say) the column mean.
Then, compute SVD to get rank-K approx for (e.g.) K=3.
Replace the missing elements with the elements of rank-K approx.
Rinse and repeat until your answer stops changing.
Voila!! I am not making this up!!
21/
Then, compute SVD to get rank-K approx for (e.g.) K=3.
Replace the missing elements with the elements of rank-K approx.
Rinse and repeat until your answer stops changing.
Voila!! I am not making this up!!
21/
The SVD is like a matrix X-ray.
For instance:
* X^T X = V D^2 V^T
* (X^T X)^{-1} = V D^{-2} V^T
* X(X^T X)^{-1} X^T = U D^{-2} U^T.
Take a minute to breathe this in.
The 1st and 2nd have no U’s, and the 3rd (hat matrix from least squares) has no V’s or D’s!
Wowzers!
22/
For instance:
* X^T X = V D^2 V^T
* (X^T X)^{-1} = V D^{-2} V^T
* X(X^T X)^{-1} X^T = U D^{-2} U^T.
Take a minute to breathe this in.
The 1st and 2nd have no U’s, and the 3rd (hat matrix from least squares) has no V’s or D’s!
Wowzers!
22/
Now, you may ask “well what about the eigen decomp?”
Well I can dispense with that concern in 1 tweet.
A symmetric matrix A (the only type worth eigendecomposing, IMO) is just $A=X^T X$ for some X.
And $X^T X = V D^2 V^T$ (see prev. tweet).
SVD >> Eigendecomp.
QED
23/
Well I can dispense with that concern in 1 tweet.
A symmetric matrix A (the only type worth eigendecomposing, IMO) is just $A=X^T X$ for some X.
And $X^T X = V D^2 V^T$ (see prev. tweet).
SVD >> Eigendecomp.
QED
23/
Not convinced? Need me to spell it out for u?
Singular vectors are the eigenvectors of $A$, and singular values are the sqrt of the eigenvalues!!!
So, the SVD gives you the eigendecomp for free!!!
EIGENDECOMPOSITION JUST GOT OWNED BY THE SVD.
That’s how it’s done!!!!!
24/
Singular vectors are the eigenvectors of $A$, and singular values are the sqrt of the eigenvalues!!!
So, the SVD gives you the eigendecomp for free!!!
EIGENDECOMPOSITION JUST GOT OWNED BY THE SVD.
That’s how it’s done!!!!!
24/
The SVD is a great 1-stop shop for data analysis.
Need to know if X is multicollinear, before fitting least squares?
Check out the singular values. If D_{11}/D_{pp} is huge then least squares is a bad idea.
If D_{pp}=0 then bad news bears, X isn’t even invertible!!
25/
Need to know if X is multicollinear, before fitting least squares?
Check out the singular values. If D_{11}/D_{pp} is huge then least squares is a bad idea.
If D_{pp}=0 then bad news bears, X isn’t even invertible!!
25/
Want to know the rank of X? It’s just # of non-zero singular values!
Want the Moore-Penrose pseudoinverse (though plz be careful — there are better ways to approximate a matrix inverse)?
That& #39;s basically the rank-K approx from earlier, but w/ 1/DD_{k} instead of DD_k!
26/
Want the Moore-Penrose pseudoinverse (though plz be careful — there are better ways to approximate a matrix inverse)?
That& #39;s basically the rank-K approx from earlier, but w/ 1/DD_{k} instead of DD_k!
26/
And please don’t troll me with your comments about how you prefer the QR or LU decompositions.
I’m a working mom with 3 kids at home in the midst of a pandemic, I know you don’t mean it, and I literally don’t have time for this.
27/
I’m a working mom with 3 kids at home in the midst of a pandemic, I know you don’t mean it, and I literally don’t have time for this.
27/
And if you prefer a specialty matrix decomposition, like NMF, then I’ve got news for you: you got fooled, because that’s just a souped up SVD. Honest to god.
28/
28/
If you remain convinced that the NMF or any other decomposition discovered in the past 80 years can hold a candle to the SVD, then I can get you a great price on a Tesla-branded vegan unicorn made out of CRISPR.
I’ll send it to you as soon as you give me all your Bitcoin.
29/
I’ll send it to you as soon as you give me all your Bitcoin.
29/
The SVD is super magical and there’s so much I’ve left unsaid.
While you can compute it using a single line of code in R or any other halfway decent programming language, it’s fun, easy, and safe to DIY w/ matrix multiplies!!!!
Check out this R code!! Wowzers!!!
30/
While you can compute it using a single line of code in R or any other halfway decent programming language, it’s fun, easy, and safe to DIY w/ matrix multiplies!!!!
Check out this R code!! Wowzers!!!
30/
I hope that this thread has helped to grow your appreciation for this magical decomposition.
The more you learn about the SVD, the more you will love it.
It will take you far on your statistics and data science journey. Godspeed.
31/31
The more you learn about the SVD, the more you will love it.
It will take you far on your statistics and data science journey. Godspeed.
31/31
A couple of typos worth correcting:
1) X(X^T X)^{-1} X^T = UU^T -- I had some extra D& #39;s floating around in there
2) To know if the matrix **X^T X** is invertible, you just have to check whether the smallest singular value is non-zero. (X itself has no inverse if n>p.)
1) X(X^T X)^{-1} X^T = UU^T -- I had some extra D& #39;s floating around in there
2) To know if the matrix **X^T X** is invertible, you just have to check whether the smallest singular value is non-zero. (X itself has no inverse if n>p.)

 Read on Twitter
Read on Twitter