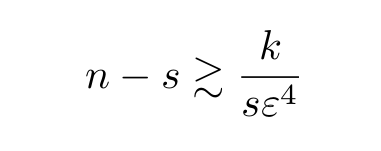Be careful what you wish for :) #statistics
1/n https://twitter.com/ccanonne_/status/1283237083260137474">https://twitter.com/ccanonne_...
So.... uniformity testing. You have n i.i.d. samples from some unknown distribution over [k]={1,2,...,k} and want to know: is it *the* uniform distribution? Or is it statistically far from it, say, at total variation distance ε?
2/n
2/n
So, before delving deeper, let& #39;s recall what total variation distance is, and formalize the question. The former is basically a measure of how distinguishable two distributions are given a single sample.
https://en.wikipedia.org/wiki/Total_variation_distance_of_probability_measures
The">https://en.wikipedia.org/wiki/Tota... latter... is below.
3/n
https://en.wikipedia.org/wiki/Total_variation_distance_of_probability_measures
The">https://en.wikipedia.org/wiki/Tota... latter... is below.
3/n
First question before I go to sleep, wake up, and continue unleashing tweets in this thread tomorrow. Just so that we& #39;re all on the same page: what is the optimal sample complexity of uniformity testing, for the whole range of k and ε (up to constant factors)?
4/n
4/n
That being said, how do we *perform* those tests? And are all tests created equal?  https://abs.twimg.com/emoji/v2/... draggable="false" alt="🧐" title="Gesicht mit Monokel" aria-label="Emoji: Gesicht mit Monokel">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🧐" title="Gesicht mit Monokel" aria-label="Emoji: Gesicht mit Monokel">
(Answer: no https://abs.twimg.com/emoji/v2/... draggable="false" alt="🍪" title="Keks" aria-label="Emoji: Keks">)
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🍪" title="Keks" aria-label="Emoji: Keks">)
For instance, I listed below a few criteria one may have in mind; there are others! Tomorrow, I& #39;ll start discussing the 7 ≠ algorithms I know...
5/n
(Answer: no
For instance, I listed below a few criteria one may have in mind; there are others! Tomorrow, I& #39;ll start discussing the 7 ≠ algorithms I know...
5/n
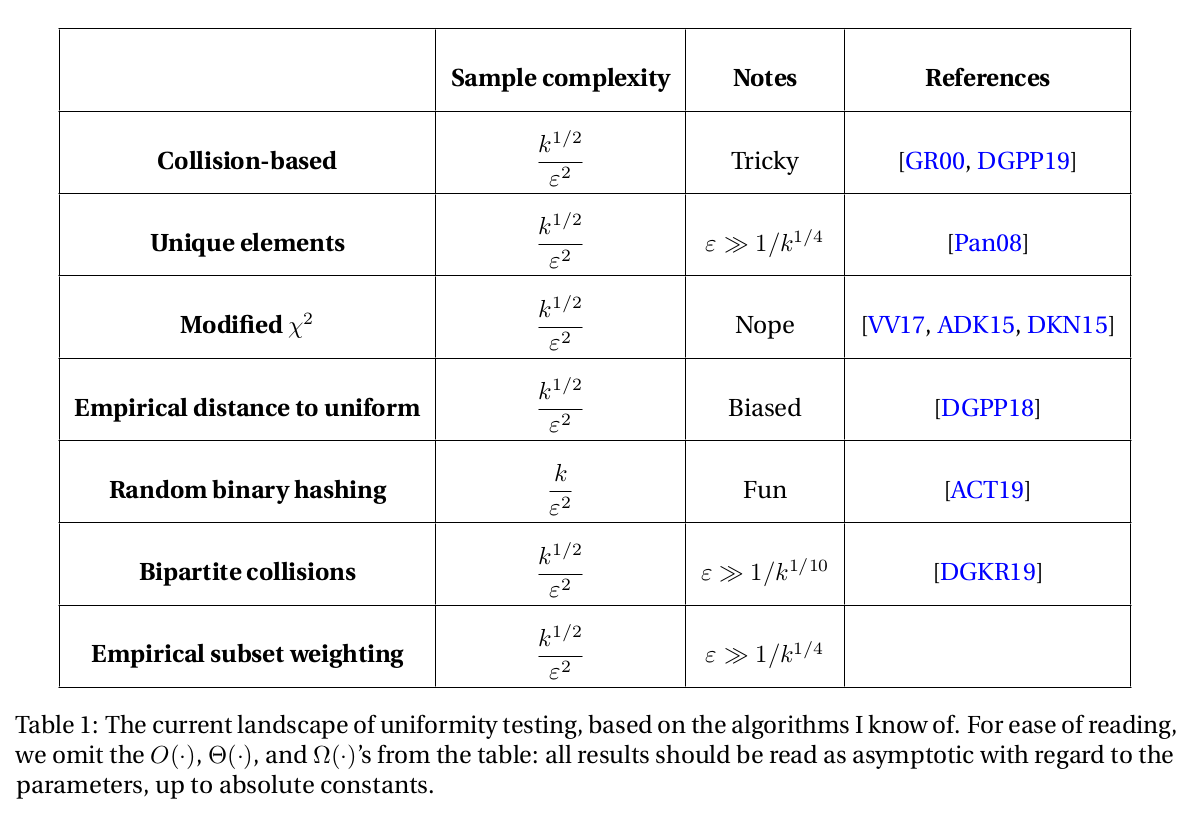
So, to resume with a table: here are the algorithms in question, with references. (Spoiler alert: the second column gives the answer to the poll above)
It& #39;ll be sprinkled through the day. Think of it as a taste of testing, if you will https://abs.twimg.com/emoji/v2/... draggable="false" alt="🥁" title="Drum" aria-label="Emoji: Drum">.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🥁" title="Drum" aria-label="Emoji: Drum">.
6/n
It& #39;ll be sprinkled through the day. Think of it as a taste of testing, if you will
6/n
So, a key idea that is central to many of those is... to "forget" about TV distance and use ℓ₂ distance as proxy. If p is ε-far from uniform (in TV) it& #39;ll be ε/√k-far in ℓ₂ distance by Cauchy—Schwarz. And the advantage of ℓ₂ is that it has a very nice interpretation!
7/n
7/n
That& #39;s the idea 4 of the 7 algorithms above rely on. Want to test uniformity of p in TV? It& #39;s enough to estimate ||p||₂² to ±ε²/k. (Estimating the squared norm is much nicer than the norm itself, as we& #39;ll see.)
So... how do we do that with only √k/ε² samples?
8/n
So... how do we do that with only √k/ε² samples?
8/n
First algorithm: collisions! Since we are looking for a natural unbiased estimator for this squared ℓ₂ norm, it& #39;s a good time to remember this nice fact.
If I take two independent samples x,y from p, the probability that x=y (a "collision") is, you guess it...
9/n
If I take two independent samples x,y from p, the probability that x=y (a "collision") is, you guess it...
9/n
This gives our first algorithm: take n samples x₁,...xₙ. For each of the {n choose 2} pairs, check if a collision occurs. Count those collisions, and use the result as unbiased estimator for ||p||₂²; threshold appropriately.
Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Fast
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Fast  https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Intuitive
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Intuitive  https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Elegant
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Elegant  https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">.
10/n
Simple
10/n
But how data-efficient is it? To analyze that, we need to know how big n must be for Z₁ to "concentrate" around its expectation ||p||₂². By Chebyshev, we need to bound the variance. Good: getting n≍√k/ε⁴ is not too hard.
Getting √k/ε².. *much* harder. "Simplicity" ☐
11/n
Getting √k/ε².. *much* harder. "Simplicity" ☐
11/n
It *is* possible to bound the variance tightly enough to get the optimal √k/ε². It& #39;s just not something I would recommend doing for fun.
Which is a uniquely good segue for our *second* algorithm, based on a dual-ish idea: counting the unique elements instead! #nocollision
12/n
Which is a uniquely good segue for our *second* algorithm, based on a dual-ish idea: counting the unique elements instead! #nocollision
12/n
(short break now, I am out of coffee)
Back to our algorithm #2: instead of collisions, what about counting the *non-collisions*, i.e., the number of elements appearing exactly once among the n samples? That& #39;& #39;ll be max for the uniform distribution, so... good? Also, easy to implement.
Call that estimator Z₂...
13/n
Call that estimator Z₂...
13/n
... the expectation is a bit unwieldy, but making a bunch of approximation it& #39;s roughly 𝔼[Z₂]≈n-n²||p||₂². Good news! We can again use that as estimator, provided we can also bound its variance...
A few tricks can help us: e.g., Efron—Stein: #Efron%E2%80%93Stein_inequality">https://en.wikipedia.org/wiki/Concentration_inequality #Efron%E2%80%93Stein_inequality
14/??">https://en.wikipedia.org/wiki/Conc...
A few tricks can help us: e.g., Efron—Stein: #Efron%E2%80%93Stein_inequality">https://en.wikipedia.org/wiki/Concentration_inequality #Efron%E2%80%93Stein_inequality
14/??">https://en.wikipedia.org/wiki/Conc...
... and that leads us to the optimal n≍√k/ε² sample complexity too! With a caveat, though: it only works for ε≫1/k¼.
Why? https://abs.twimg.com/emoji/v2/... draggable="false" alt="🤔" title="Denkendes Gesicht" aria-label="Emoji: Denkendes Gesicht">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🤔" title="Denkendes Gesicht" aria-label="Emoji: Denkendes Gesicht">
15/n
Why?
15/n
Spoiler: not the  https://abs.twimg.com/emoji/v2/... draggable="false" alt="🦄" title="Einhorngesicht" aria-label="Emoji: Einhorngesicht">. We count the number of unique elements, and there can& #39;t be more than k of them if the domain size is k. If we take n too large, we start having to ignore many samples.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🦄" title="Einhorngesicht" aria-label="Emoji: Einhorngesicht">. We count the number of unique elements, and there can& #39;t be more than k of them if the domain size is k. If we take n too large, we start having to ignore many samples.
So we need n ≪ k, or things start to break. Since n≍√k/ε², that gives ε≫1/k¼...
16/n
So we need n ≪ k, or things start to break. Since n≍√k/ε², that gives ε≫1/k¼...
16/n
To summarize the "unique elements algorithm", Algo #2:
Data efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Time efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Simple + "simple" https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
... but has a restriction on the parameters ☐
17/n
Data efficient
Time efficient
Simple + "simple"
Elegant
... but has a restriction on the parameters ☐
17/n
(Cool, I& #39;m done with algo 2 out of 7 and it& #39;s only been 17 tweets so far. I may wrap up before n=100. Time for a  https://abs.twimg.com/emoji/v2/... draggable="false" alt="☕" title="Heißgetränk" aria-label="Emoji: Heißgetränk"> break!)
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☕" title="Heißgetränk" aria-label="Emoji: Heißgetränk"> break!)
(Since I& #39;ve been asked: no, I am not drinking a coffee per hour. I made coffee earlier, but it& #39;s a slow process: it& #39;s done now, time to drink it.)
Now onto algorithm #3. If you are a statistician, or just took #Stats 101, or just got lost on @Wikipedia at some point and ended up on the wrong page, you may know of Pearson’s χ² test for goodness-of-fit: let Nᵢ be the # of times i appears in the sample. Compute:
18/n
18/n
Then sit back and relax. Bad news: that does not actually lead to the optimal sample complexity: the variance of this thing can be too big, due to elements we only see zero or one time (so... most of them). The good news is that a simple "corrected" variant *will* work!
19/n
19/n
Why is that? When computing the variance, many Nᵢ terms will cancel if you only see an element i zero or one time, so the variance goes down. For the analysis, it’s helpful to think of taking Poisson(n) samples  https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐟" title="Fisch" aria-label="Emoji: Fisch"> instead of exactly n, as it simplifies things (and...
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐟" title="Fisch" aria-label="Emoji: Fisch"> instead of exactly n, as it simplifies things (and...
20/n
20/n
... changes ≈ nothing else here). Then the Nᵢs become independent, with Nᵢ ∼ Poisson(npᵢ) (that not magic, it’s  https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐟" title="Fisch" aria-label="Emoji: Fisch">). The expectation is exactly what we& #39;d hope for, and bounding the variance is not insane either thanks to Poissonization—so Chebyshev, here we come!
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐟" title="Fisch" aria-label="Emoji: Fisch">). The expectation is exactly what we& #39;d hope for, and bounding the variance is not insane either thanks to Poissonization—so Chebyshev, here we come!
21/n
21/n
(As an exercise, though, compute the variance *without* that "-Nᵢ" term. Things don& #39;t go so well.) Great, we get the optimal n≍√k/ε² here too. But... it& #39;s not really beautiful, is it?
Data efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
"Simple" https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Intuitive ☐
Elegant ☐
22/n
Data efficient
Simple
"Simple"
Fast
Intuitive ☐
Elegant ☐
22/n
Time for our 4th algorithm! Let& #39;s take a break from ℓ₂ as proxy for TV and consider another, very natural thing: the *plugin estimator*. Given n samples from p, we can compute the empirical distribution, call that p̂. Now, recall we want to test the thing below:
23/n
23/n
Why not simply plugin p̂ instead of p in the distance, compute that, and hope for the best?
A reason might be: *this sounds like a terrible idea!* Unless n=Ω(k) (much more than what we want), the empirical p̂ will be at TV distance 1-o(1) from uₖ, even if p *is* uₖ.
24/n
A reason might be: *this sounds like a terrible idea!* Unless n=Ω(k) (much more than what we want), the empirical p̂ will be at TV distance 1-o(1) from uₖ, even if p *is* uₖ.
24/n
That’s the thing, though: hell is in the o(1). Sure, 𝔼[Z₄] ≈1 whether p is uniform or far from it unless n=Ω(k). But this "≈" will be different in the two cases!
Carefully analyzing this tiny gap in 𝔼+showing that Z₄ concentrates well enough to preserve it... works!
25/n
Carefully analyzing this tiny gap in 𝔼+showing that Z₄ concentrates well enough to preserve it... works!
25/n
That it works at all (let alone results in the optimal n≍√k/ε²) is a real source of wonder to me. It also has nice properties (e.g., low "sensitivity")!
The analysis is not really simple, though...
Data efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
"Simple" ☐
Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Intuitive ☐
Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
26/n
The analysis is not really simple, though...
Data efficient
Simple
"Simple" ☐
Fast
Intuitive ☐
Elegant
26/n
Now a tester that is *not* sample-optimal (but has other advantages, and is quite cute): Algo #5, "random binary hashing."
 https://abs.twimg.com/emoji/v2/... draggable="false" alt="💡" title="Elektrische Glühbirne" aria-label="Emoji: Elektrische Glühbirne">If there is one thing we know how to do, it& #39;s estimating the bias of a coin. We don& #39;t have a coin here, we have a glorious (k-1)-dimensional object.
https://abs.twimg.com/emoji/v2/... draggable="false" alt="💡" title="Elektrische Glühbirne" aria-label="Emoji: Elektrische Glühbirne">If there is one thing we know how to do, it& #39;s estimating the bias of a coin. We don& #39;t have a coin here, we have a glorious (k-1)-dimensional object.
27/n
27/n
Hell, let& #39;s just randomly make it a coin, shall we? Pick your favorite random hash function h: [k]→{0,1}, which partitioning the domain in two sets S₀, S₁.
Hash all the n samples you got: NOW we have a random coin!
28/n
Hash all the n samples you got: NOW we have a random coin!
28/n
Let& #39;s estimate its bias then: we know exactly what this should be under uniform: uₖ(S₀). If only we could argue that p(S₀)≉uₖ(S₀) (with high proba over the choice of the hash function) whenever TV(p,uₖ)>ε, we& #39;d be good.
Turns out... it is the case. Hurray :)
29/n
Turns out... it is the case. Hurray :)
29/n
So we can just do exactly this: we need to estimate the bias p(S₀) up to ±ε/√k. This can be done with n≍k/ε² samples (coin flips), as desired.
Not optimal, but... pretty fun.
Data efficient ☐
Memory efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
"Simple" https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Intuitive https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
30/n
Not optimal, but... pretty fun.
Data efficient ☐
Memory efficient
Simple
"Simple"
Fast
Intuitive
Elegant
30/n
(Five algorithms out of seven so far, time for a break. I& #39;m still missing Sleepy and Happy—more when I return!)
In the meantime: what do you care more about?
In the meantime: what do you care more about?
Let& #39;s continue! Algorithm #6: "Bipartite collision tester."
In our first, "collision-based" algorithm, recall that we took a multiset S of n samples from p and looked at the number of "collisions" in S to define our statistic Z₁. That gave us an estimator for ||p||₂²...
31/n
In our first, "collision-based" algorithm, recall that we took a multiset S of n samples from p and looked at the number of "collisions" in S to define our statistic Z₁. That gave us an estimator for ||p||₂²...
31/n
... which is fine, but required to keep in memory all the samples observed so far. Expensive.
One related idea would be to instead take *two* multisets S₁, S₂ of n₁ and n₂ samples, and only count "bipartite collisions", b/w samples in S₁ and samples in S₂:
32/n
One related idea would be to instead take *two* multisets S₁, S₂ of n₁ and n₂ samples, and only count "bipartite collisions", b/w samples in S₁ and samples in S₂:
32/n
That still has the right expectation 𝔼[Z₅]=||p||₂². Back to ℓ₂ as proxy! Compared to the "vanilla" collision-based test, this
is more flexible: S₁,S₂ can be of ≠ size, so that lends itself to some settings where a tradeoff between n₁ and n₂ is desirable. We need:
33/n
is more flexible: S₁,S₂ can be of ≠ size, so that lends itself to some settings where a tradeoff between n₁ and n₂ is desirable. We need:
33/n
As well as some other (annoying) technical condition (maybe not necessary?). For the case n₁=n₂, we get back the optimal n≍√k/ε², as long as [technical annoying condition] ε≫1/k^(1/10).
Not bad!
Data efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
"Simple" ☐
Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Intuitive ☐
Elegant ☐
34/n
Not bad!
Data efficient
Simple
"Simple" ☐
Fast
Intuitive ☐
Elegant ☐
34/n
Stay tuned for the very last algorithm. Spoiler: it is adaptive!
Here we go! Last algo: "empirical subset weighting." That one I really like. It& #39;s adaptive, it& #39;s weird, and (I think) it& #39;s new (h/t @AcharyaJayadev, @hstyagi, and @SZiteng)
Fix s < n. Take n samples from p, and consider the set S (not multiset) of by the first s samples.
35/n
Fix s < n. Take n samples from p, and consider the set S (not multiset) of by the first s samples.
35/n
Let& #39;s consider the random variable p(S). Its expectation (see below) is (making a bunch of approximations) 𝔼[p(S)]≈s||p||₂².
Great: we have a new estimator for (roughly) the squared ℓ₂ norm! Assuming things went well and p(S) concentrates around its expectation, ...
36/n
Great: we have a new estimator for (roughly) the squared ℓ₂ norm! Assuming things went well and p(S) concentrates around its expectation, ...
36/n
... at the end of this first stage we have S s.t. p(S) is either ≈s/k or ≈s(1+Ω(ε²))/k. Neat... a biased coin problem!
Let& #39;s do a second stage then. Take the next n-s samples, check which ones fall in S, use that to estimate p(S) to ±sε²/k.
You can do that as long as:
37/n
Let& #39;s do a second stage then. Take the next n-s samples, check which ones fall in S, use that to estimate p(S) to ±sε²/k.
You can do that as long as:
37/n
(sanity check: why?) So in particular, for s=n/2 we get the optimal n≍√k/ε². Hurray!
OK, there is the same slight bummer as in the "unique elements" algorithm: we need s ≪ k in the first stage (can you see why?), so overall this requires ε ≫ 1/k¼. Oh, well.
38/n
OK, there is the same slight bummer as in the "unique elements" algorithm: we need s ≪ k in the first stage (can you see why?), so overall this requires ε ≫ 1/k¼. Oh, well.
38/n
To summarize our last, "empirical subset weighting" algorithm:
Data efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Memory efficient https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
"Simple" ☐ (jury& #39;s still out)
Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Intuitive https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">
Yes, I& #39;m a bit biased, I know.
39/n
Data efficient
Memory efficient
Simple
"Simple" ☐ (jury& #39;s still out)
Fast
Intuitive
Elegant
Yes, I& #39;m a bit biased, I know.
39/n
Anyways, this concludes this giant thread! Hope you enjoyed it—feel free to comment or ask questions below. ↴
I& #39;ll put up a https://abs.twimg.com/emoji/v2/... draggable="false" alt="📝" title="Memo" aria-label="Emoji: Memo"> summary soon. In the meantime, here are a subset of the algorithms mentioned: which one do *you* prefer?
https://abs.twimg.com/emoji/v2/... draggable="false" alt="📝" title="Memo" aria-label="Emoji: Memo"> summary soon. In the meantime, here are a subset of the algorithms mentioned: which one do *you* prefer?  https://abs.twimg.com/emoji/v2/... draggable="false" alt="🙋" title="Glückliche Person, die eine Hand hebt" aria-label="Emoji: Glückliche Person, die eine Hand hebt">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🙋" title="Glückliche Person, die eine Hand hebt" aria-label="Emoji: Glückliche Person, die eine Hand hebt">
40/end
I& #39;ll put up a
40/end

 Read on Twitter
Read on Twitter
 (Answer: no https://abs.twimg.com/emoji/v2/... draggable="false" alt="🍪" title="Keks" aria-label="Emoji: Keks">)For instance, I listed below a few criteria one may have in mind; there are others! Tomorrow, I& #39;ll start discussing the 7 ≠ algorithms I know... 5/n" title="That being said, how do we *perform* those tests? And are all tests created equal? https://abs.twimg.com/emoji/v2/... draggable="false" alt="🧐" title="Gesicht mit Monokel" aria-label="Emoji: Gesicht mit Monokel">(Answer: no https://abs.twimg.com/emoji/v2/... draggable="false" alt="🍪" title="Keks" aria-label="Emoji: Keks">)For instance, I listed below a few criteria one may have in mind; there are others! Tomorrow, I& #39;ll start discussing the 7 ≠ algorithms I know... 5/n" class="img-responsive" style="max-width:100%;"/>
(Answer: no https://abs.twimg.com/emoji/v2/... draggable="false" alt="🍪" title="Keks" aria-label="Emoji: Keks">)For instance, I listed below a few criteria one may have in mind; there are others! Tomorrow, I& #39;ll start discussing the 7 ≠ algorithms I know... 5/n" title="That being said, how do we *perform* those tests? And are all tests created equal? https://abs.twimg.com/emoji/v2/... draggable="false" alt="🧐" title="Gesicht mit Monokel" aria-label="Emoji: Gesicht mit Monokel">(Answer: no https://abs.twimg.com/emoji/v2/... draggable="false" alt="🍪" title="Keks" aria-label="Emoji: Keks">)For instance, I listed below a few criteria one may have in mind; there are others! Tomorrow, I& #39;ll start discussing the 7 ≠ algorithms I know... 5/n" class="img-responsive" style="max-width:100%;"/>
 .6/n" title="So, to resume with a table: here are the algorithms in question, with references. (Spoiler alert: the second column gives the answer to the poll above)It& #39;ll be sprinkled through the day. Think of it as a taste of testing, if you will https://abs.twimg.com/emoji/v2/... draggable="false" alt="🥁" title="Drum" aria-label="Emoji: Drum">.6/n" class="img-responsive" style="max-width:100%;"/>
.6/n" title="So, to resume with a table: here are the algorithms in question, with references. (Spoiler alert: the second column gives the answer to the poll above)It& #39;ll be sprinkled through the day. Think of it as a taste of testing, if you will https://abs.twimg.com/emoji/v2/... draggable="false" alt="🥁" title="Drum" aria-label="Emoji: Drum">.6/n" class="img-responsive" style="max-width:100%;"/>
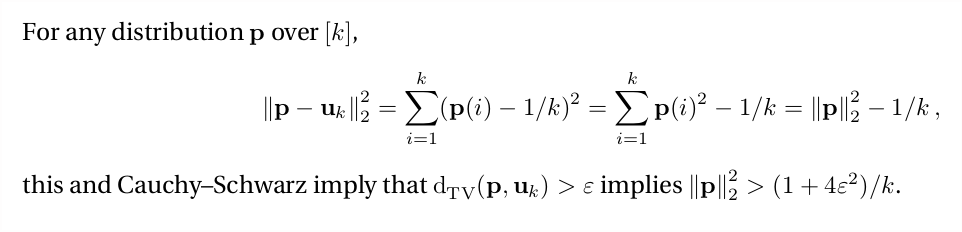
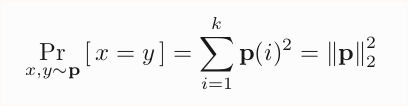
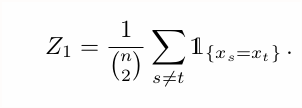 . Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Intuitive https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">.10/n" title="This gives our first algorithm: take n samples x₁,...xₙ. For each of the {n choose 2} pairs, check if a collision occurs. Count those collisions, and use the result as unbiased estimator for ||p||₂²; threshold appropriately.Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Intuitive https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">.10/n" class="img-responsive" style="max-width:100%;"/>
. Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Intuitive https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">.10/n" title="This gives our first algorithm: take n samples x₁,...xₙ. For each of the {n choose 2} pairs, check if a collision occurs. Count those collisions, and use the result as unbiased estimator for ||p||₂²; threshold appropriately.Simple https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Fast https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Intuitive https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">. Elegant https://abs.twimg.com/emoji/v2/... draggable="false" alt="☑️" title="Kästchen mit Häkchen" aria-label="Emoji: Kästchen mit Häkchen">.10/n" class="img-responsive" style="max-width:100%;"/>
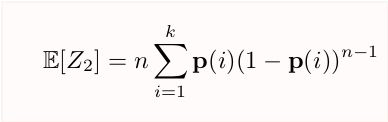
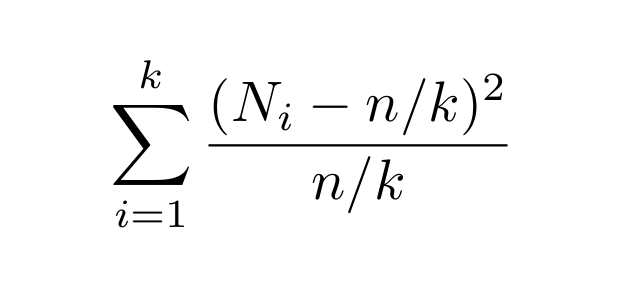
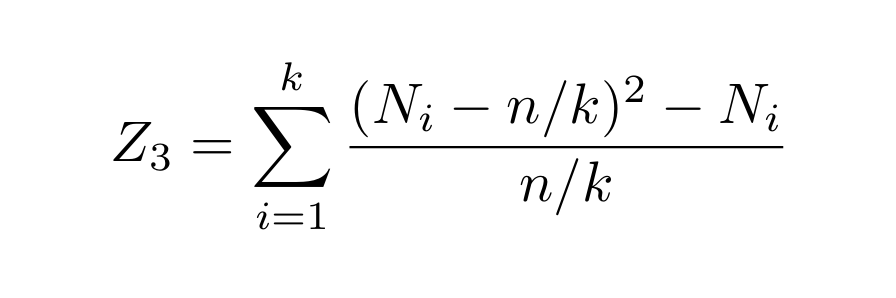
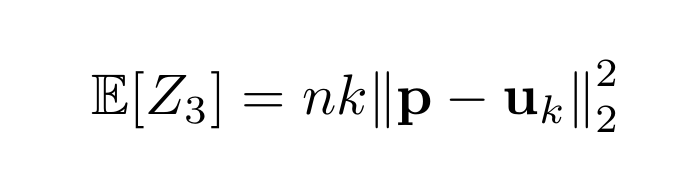 ). The expectation is exactly what we& #39;d hope for, and bounding the variance is not insane either thanks to Poissonization—so Chebyshev, here we come!21/n" title="... changes ≈ nothing else here). Then the Nᵢs become independent, with Nᵢ ∼ Poisson(npᵢ) (that not magic, it’s https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐟" title="Fisch" aria-label="Emoji: Fisch">). The expectation is exactly what we& #39;d hope for, and bounding the variance is not insane either thanks to Poissonization—so Chebyshev, here we come!21/n" class="img-responsive" style="max-width:100%;"/>
). The expectation is exactly what we& #39;d hope for, and bounding the variance is not insane either thanks to Poissonization—so Chebyshev, here we come!21/n" title="... changes ≈ nothing else here). Then the Nᵢs become independent, with Nᵢ ∼ Poisson(npᵢ) (that not magic, it’s https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐟" title="Fisch" aria-label="Emoji: Fisch">). The expectation is exactly what we& #39;d hope for, and bounding the variance is not insane either thanks to Poissonization—so Chebyshev, here we come!21/n" class="img-responsive" style="max-width:100%;"/>
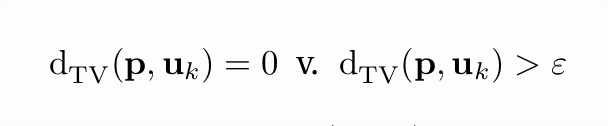
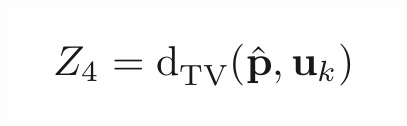
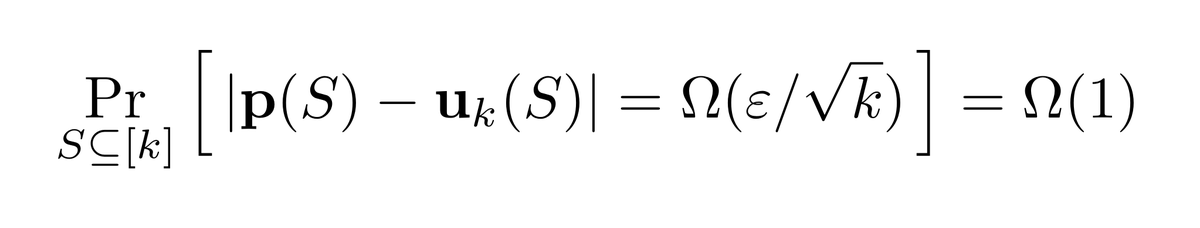
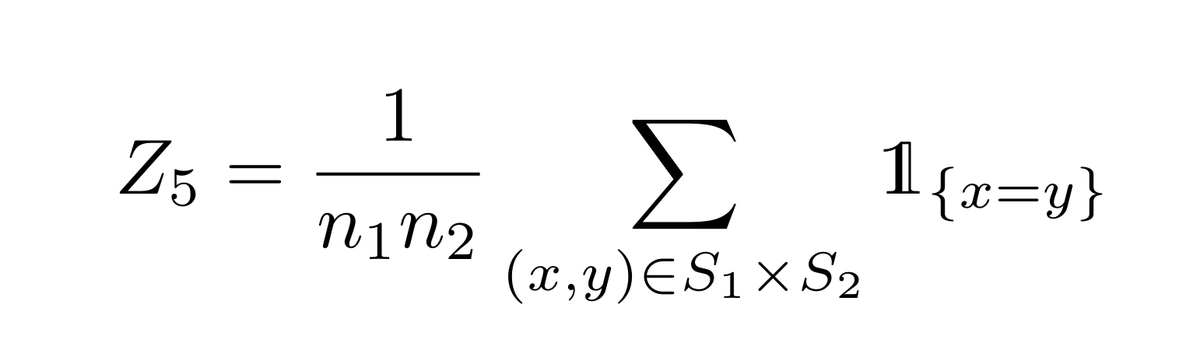
![That still has the right expectation 𝔼[Z₅]=||p||₂². Back to ℓ₂ as proxy! Compared to the "vanilla" collision-based test, thisis more flexible: S₁,S₂ can be of ≠ size, so that lends itself to some settings where a tradeoff between n₁ and n₂ is desirable. We need:33/n That still has the right expectation 𝔼[Z₅]=||p||₂². Back to ℓ₂ as proxy! Compared to the "vanilla" collision-based test, thisis more flexible: S₁,S₂ can be of ≠ size, so that lends itself to some settings where a tradeoff between n₁ and n₂ is desirable. We need:33/n](https://pbs.twimg.com/media/EdFI9wFUYAAewly.png)
![Let& #39;s consider the random variable p(S). Its expectation (see below) is (making a bunch of approximations) 𝔼[p(S)]≈s||p||₂².Great: we have a new estimator for (roughly) the squared ℓ₂ norm! Assuming things went well and p(S) concentrates around its expectation, ...36/n Let& #39;s consider the random variable p(S). Its expectation (see below) is (making a bunch of approximations) 𝔼[p(S)]≈s||p||₂².Great: we have a new estimator for (roughly) the squared ℓ₂ norm! Assuming things went well and p(S) concentrates around its expectation, ...36/n](https://pbs.twimg.com/media/EdFUhSYUcAAl3wk.png)