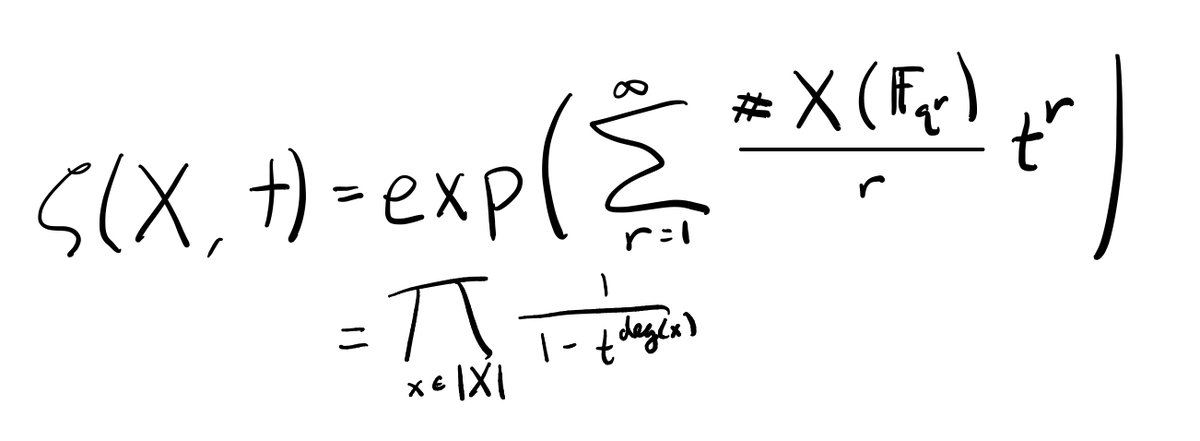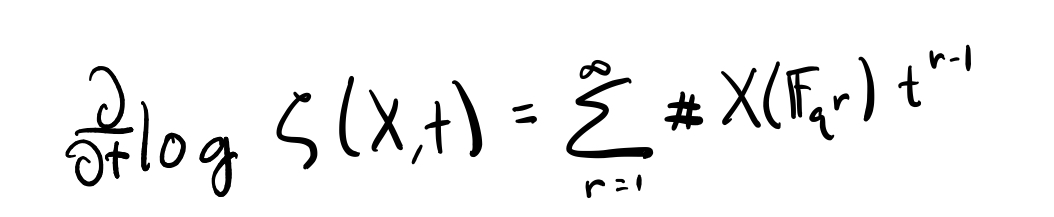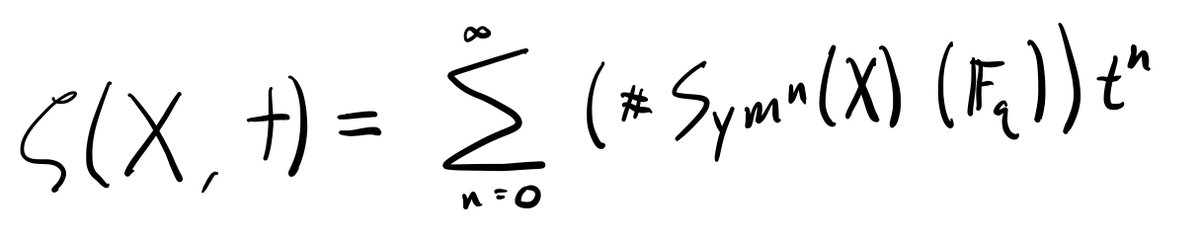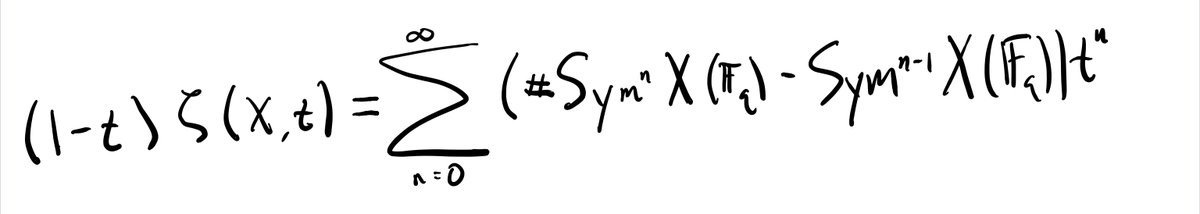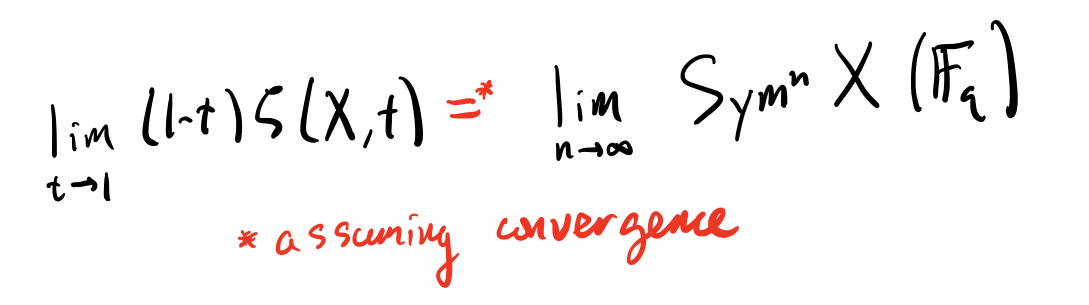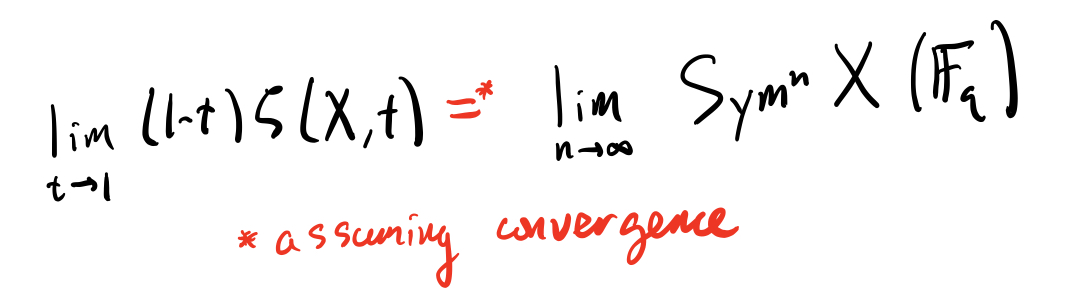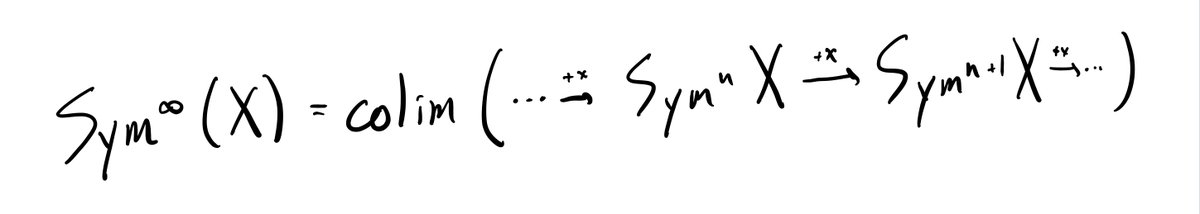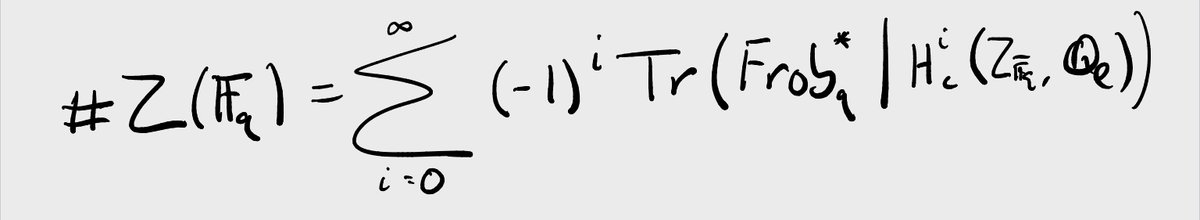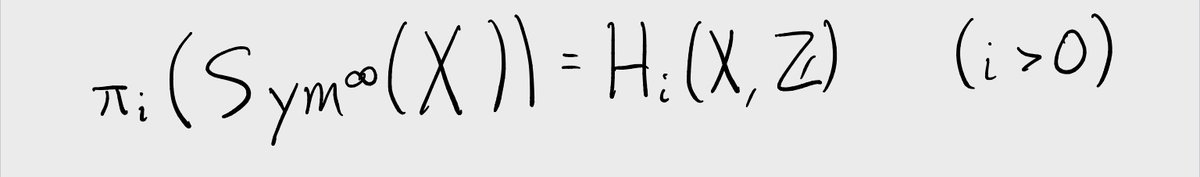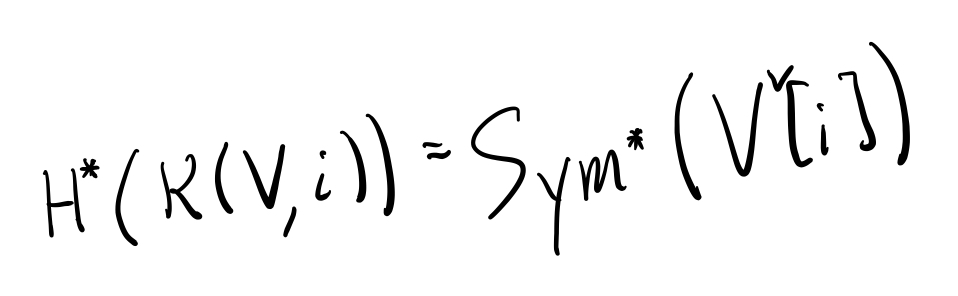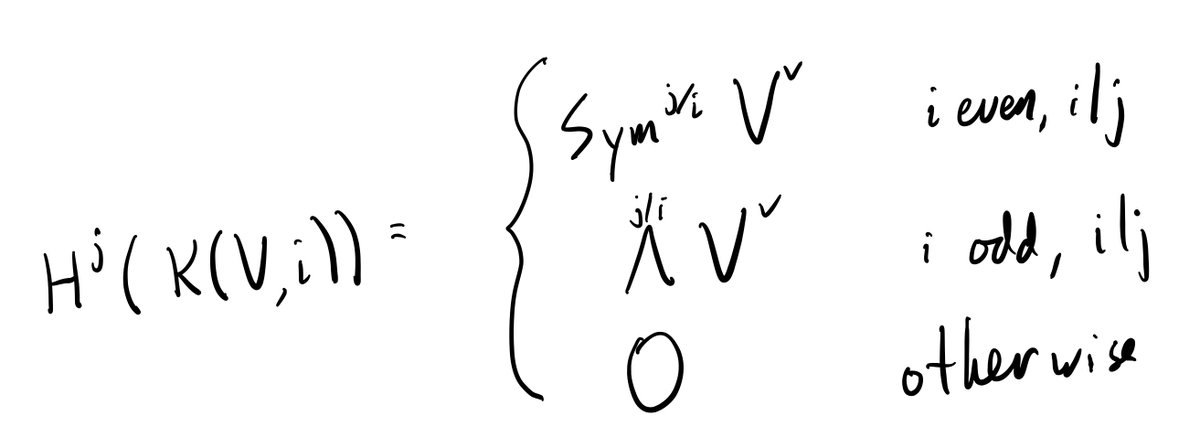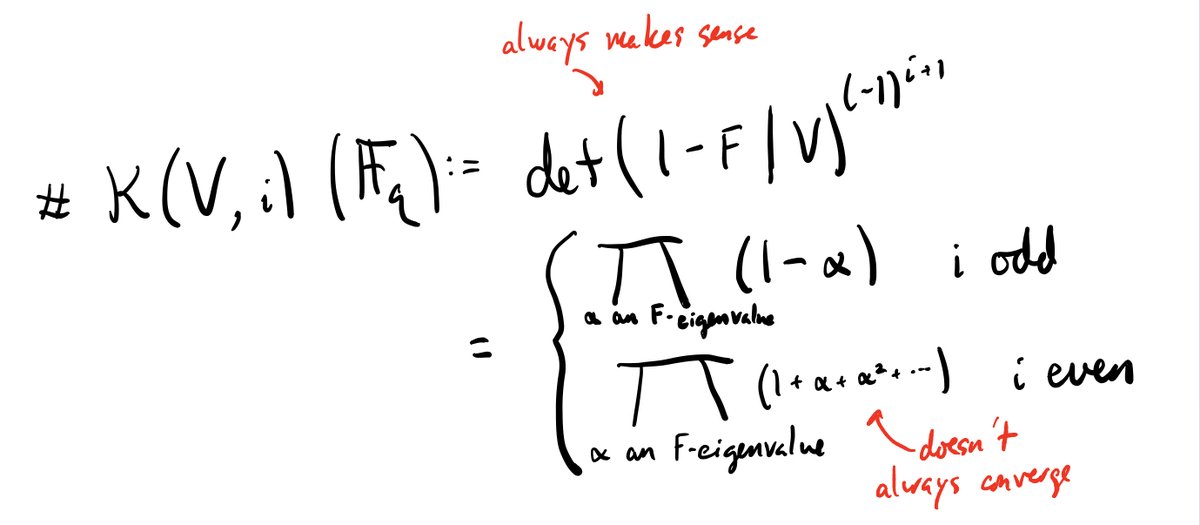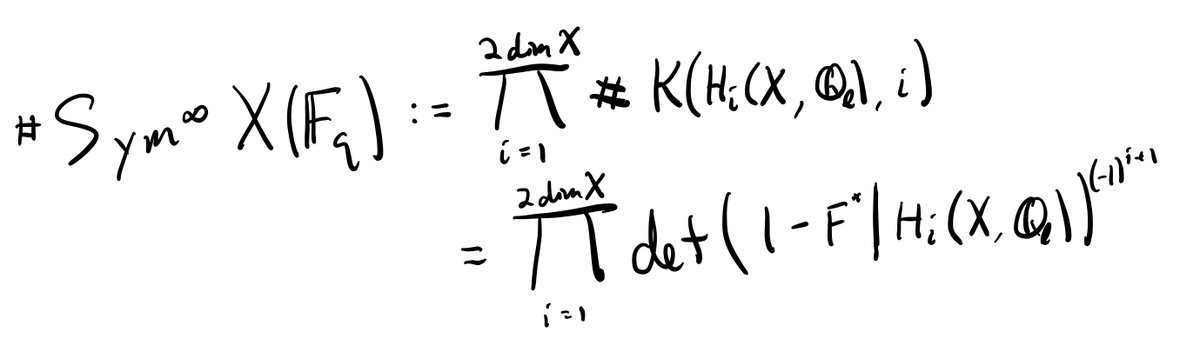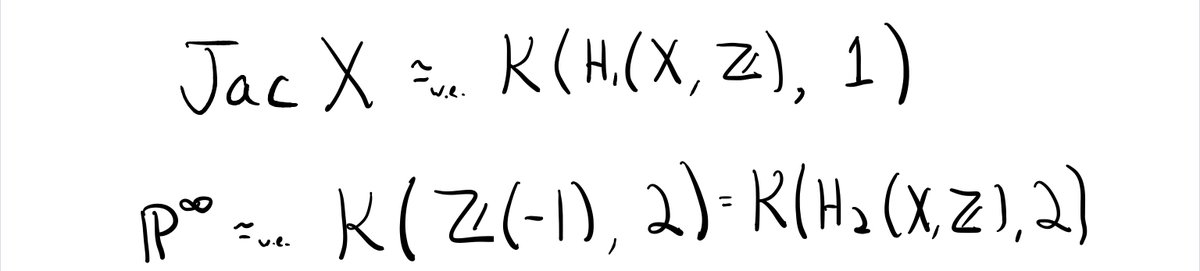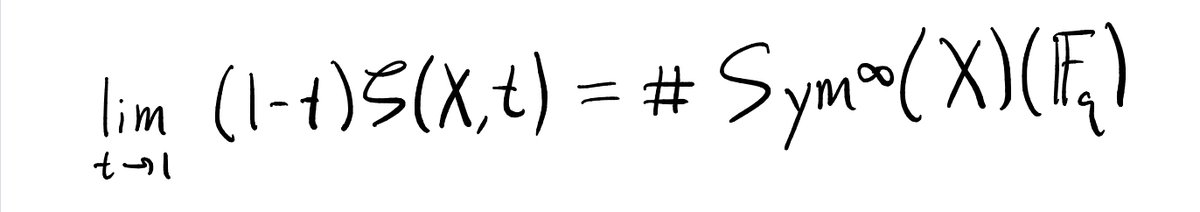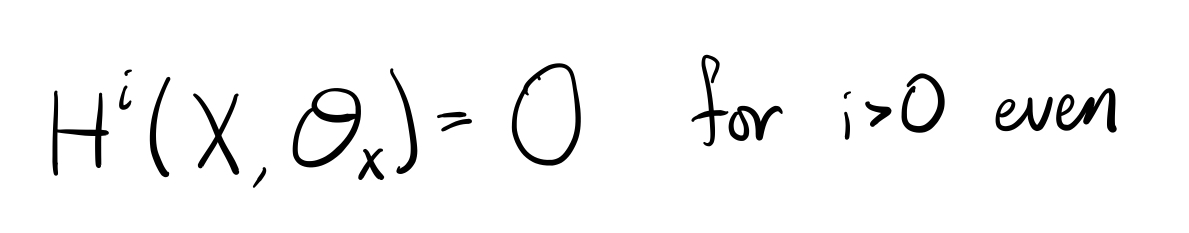Thread, lost due to computer crash and recreated: a mysterious connection between number theory (the analytic class number formula) and algebraic topology (the Dold-Thom theorem). 1/n
The class number formula (below, from Wikipedia) tells us that the residue of the Dedekind zeta function of a number field K at s=1 is related to certain more algebraic invariants of the number field -- for example, its class number h_K and the number of roots of unity in K. 2/n
If you don& #39;t know what the Dedekind zeta function of a number field is, that& #39;s alright -- we& #39;ll replace it with a simpler object soon. It’s a generalization of the Riemann zeta function (the Dedekind zeta function of ℚ); the actual definition is below. 3/n
So here’s our "toy" model: the zeta function of a variety over a finite field. Let X/𝔽_q be a variety, defined by a bunch of polynomial equations with coefficients in 𝔽_q. The zeta function (below) records how many solutions these equations have over extensions of 𝔽_q. 4/n
Like the Riemann zeta function (and Dedekind zeta functions) this zeta function has an Euler product. In good cases it has a functional equation and some version of the Riemann hypothesis; it is the subject of the Weil conjectures, proven by Dwork, Grothendieck, and Deligne. 5/n
If the definition looks weird, note that its logarithmic derivative (below) is a generating series counting points of X over finite extensions of 𝔽_q. Slogan: the zeros and poles of a meromorphic function control the growth of the coefficients of its logarithmic derivative. 6/n
Before we dig into the analytic class number formula for this zeta function, we need a different description of it. Let Sym^n(X) be the quotient of X^n by the permutation action of the symmetric group on n letters. A point of Sym^n(X) is called an effective 0-cycle. 7/n
𝔽_q-points of Sym^n(X) ("rational effective 0-cycles") have a simple description; they& #39;re collections of Galois orbits of 𝔽_q-bar points of X with total size n. The Euler product description of zeta shows that it& #39;s a generating function for rational effective 0-cycles on X! 8/n
(9/n) Now let’s compute the residue of this zeta function at t=1. To do this, we multiply by (1-t) and take the limit as t-->1.
Multiplying by (1-t) gives:
Multiplying by (1-t) gives:
(10/n) Now if t=1 is in the radius of convergence of this power series, we can just compute the limit by evaluating at t=1. The sum we get telescopes, giving the following equality (again, assuming the limit on the right makes sense):
OK, but this limit *never* exists, right? It’s the limit of an increasing sequence of integers, so we’re SOL.
Except that sometimes the limit exists p-adically! 11/n
Except that sometimes the limit exists p-adically! 11/n
Let& #39;s try an example. Suppose C/𝔽_q is a smooth proper curve of genus g. Then for n>>0, the Riemann-Roch theorem tells us that Sym^n(C) is a ℙ^{n-g}-bundle over Jac(X), the Jacobian of X. 12/n
So for n>>0, we can count the 𝔽_q-points of Sym^n(C): there are
|Jac(C)(𝔽_q)|(1+q+q^2+...+q^{n-g})
of them, because there are evidently |Jac(C)(𝔽_q)| points of Jac(C), and ℙ^{n-g} has (1+q+q^2+...+q^{n-g}) 𝔽_q-points. 13/n
|Jac(C)(𝔽_q)|(1+q+q^2+...+q^{n-g})
of them, because there are evidently |Jac(C)(𝔽_q)| points of Jac(C), and ℙ^{n-g} has (1+q+q^2+...+q^{n-g}) 𝔽_q-points. 13/n
Now if p is the characteristic of 𝔽_q, this converges p-adically as one takes n to ∞, because q is divisible by p; in fact, it converges to
|Jac(C)(𝔽_q)|/(1-q). 14/n
|Jac(C)(𝔽_q)|/(1-q). 14/n
I claim that this is the class number formula for curves over finite fields.
Note that |Jac(C)(𝔽_q)| is the class group of C, and (1-q) is (up to a sign) the number of roots of unity in the ring of functions on our curve, just like with number fields. 15/n
Note that |Jac(C)(𝔽_q)| is the class group of C, and (1-q) is (up to a sign) the number of roots of unity in the ring of functions on our curve, just like with number fields. 15/n
For the rest of this thread, I want to try to make sense of the equation below, even when the limit does not converge, using ideas from algebraic topology: the Dold-Thom theorem. That is, I want to explain how the "class number formula" counts points on a certain space. 16/n
Choose x in X(𝔽_q). This gives us maps
Sym^n(X)-->Sym^{n+1}(X),
just by adding x to an n-tuple of points, to get an (n+1)-tuple. The infinite symmetric power Sym^∞(X) will be the union of all of the Sym^n(X).
17/n
Sym^n(X)-->Sym^{n+1}(X),
just by adding x to an n-tuple of points, to get an (n+1)-tuple. The infinite symmetric power Sym^∞(X) will be the union of all of the Sym^n(X).
17/n
Let& #39;s try to "count points" on this infinite-dimensional space Sym^∞(X). We can& #39;t do this naively; in any reasonable sense, this space has infinitely many points. Instead, we& #39;ll use the Grothendieck-Lefschetz trace formula, which tells us to count points using cohomology. 18/n
Taking Z above to be Sym^∞(X), we& #39;ll almost always get an infinite sum, but we& #39;ll find a way to regularize it.
So the question becomes: what& #39;s the cohomology of Sym^∞(X)? The answer -- given by the Dold-Thom theorem -- is well known to topologists. 19/n
So the question becomes: what& #39;s the cohomology of Sym^∞(X)? The answer -- given by the Dold-Thom theorem -- is well known to topologists. 19/n
The Dold-Thom theorem tells us that for a connected CW complex X, the i-th homotopy group of Sym^∞(X) is the same as the i-th singular homology group of X (as long as i is positive). We can use this to compute the (rational) cohomology of X. 20/n
For the purpose of computing rational homology (which is all the Grothendieck-Lefschetz trace formula cares about) we can pretend the infinite symmetric power is a product of Eilenberg-Maclane spaces. 21/n
So let& #39;s try to "count points" on K(V,i), where V is a vector space with Frobenius action. To do this, we& #39;ll compute the cohomology of K(V,i) and apply the Grothendieck-Lefschetz trace formula. Then we& #39;ll try to make sense of what comes out. 22/n
We know what the cohomology of K(V,i) is, though -- it& #39;s the following symmetric algebra (taken in the graded-commutative sense). I& #39;ll be more explicit in the next tweet. 23/n
(24/n) Explicitly, the cohomology of K(V,i) is given by the following formula (which depends on the parity of i):
Formally applying the Grothendieck-Lefschetz trace formula (if V is a vector space with Frobenius action) gives the second line below, which doesn& #39;t always make sense if i is even. But using the formula for a geometric series, we get the first line, which always makes sense! 25/n
Now that we& #39;ve come up with a reasonable definition for the number of points on K(V,i), we can (using Dold-Thom as motivation) make an analogous definition for Sym^∞(X). 26/n
(27/n) Namely, since Sym^∞(X) is (for our purposes) a product of Eilenberg-Maclane spaces, we& #39;ll just *define* its point count to be the product of the corresonding point counts. That is:
(28/n) Let& #39;s see this at work for curves. Remember that the infinite symmetric power of a curve was a (infinite) projective space bundle over the Jacobian over the curve. But over ℂ, ℙ^∞ and the Jacobian are both Eilenberg-Maclane spaces:
Moreover our new definition of a "point count" for Sym^∞(X) gives precisely
|Jac(X)(𝔽_q)|/(1-q).
That is, it& #39;s our "class number formula" from before. (29/n)
|Jac(X)(𝔽_q)|/(1-q).
That is, it& #39;s our "class number formula" from before. (29/n)
Now here& #39;s the punchline. For any smooth projective variety over 𝔽_q whatsoever, the residue at t=1 of the zeta function is *always* the "number of points" of Sym^∞(X), under our definition via Dold-Thom. We& #39;ve found a geometric interpretation of the class number formula. 30/n
Note that this is true even when the limit from before doesn& #39;t converge p-adically (for example, the limit doesn& #39;t converge for most K3 surfaces). It& #39;s an algebro-geometric avatar of Dold-Thom. 31/n

 Read on Twitter
Read on Twitter