I just released my first #Rstats package  https://abs.twimg.com/emoji/v2/... draggable="false" alt="📦" title="Paket" aria-label="Emoji: Paket">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="📦" title="Paket" aria-label="Emoji: Paket">
Here& #39;s a quick rundown on how you can use the {metameta} package to effortlessly calculate the statistical power of published meta-analyses to better understand the evidential value of included studies
https://github.com/dsquintana/metameta">https://github.com/dsquintan...
Here& #39;s a quick rundown on how you can use the {metameta} package to effortlessly calculate the statistical power of published meta-analyses to better understand the evidential value of included studies
https://github.com/dsquintana/metameta">https://github.com/dsquintan...
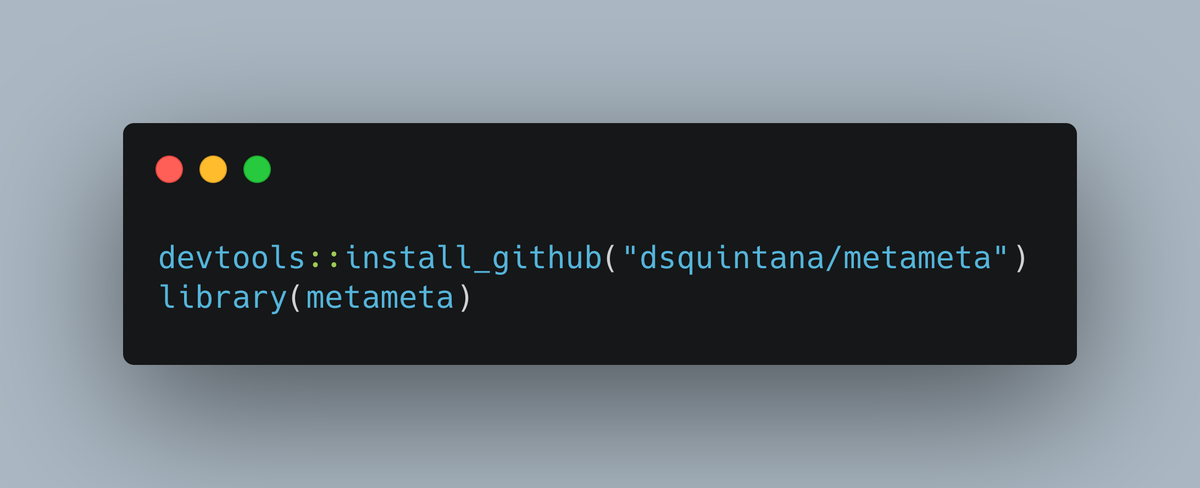
First we& #39;ll install the package via Github and then load it.
The package contains two main features:
1. Functions to calculate the statistical power of studies in a meta-analysis
2. A function to create a Firepower plot, which visualises statistical power across meta-analyses
The package contains two main features:
1. Functions to calculate the statistical power of studies in a meta-analysis
2. A function to create a Firepower plot, which visualises statistical power across meta-analyses
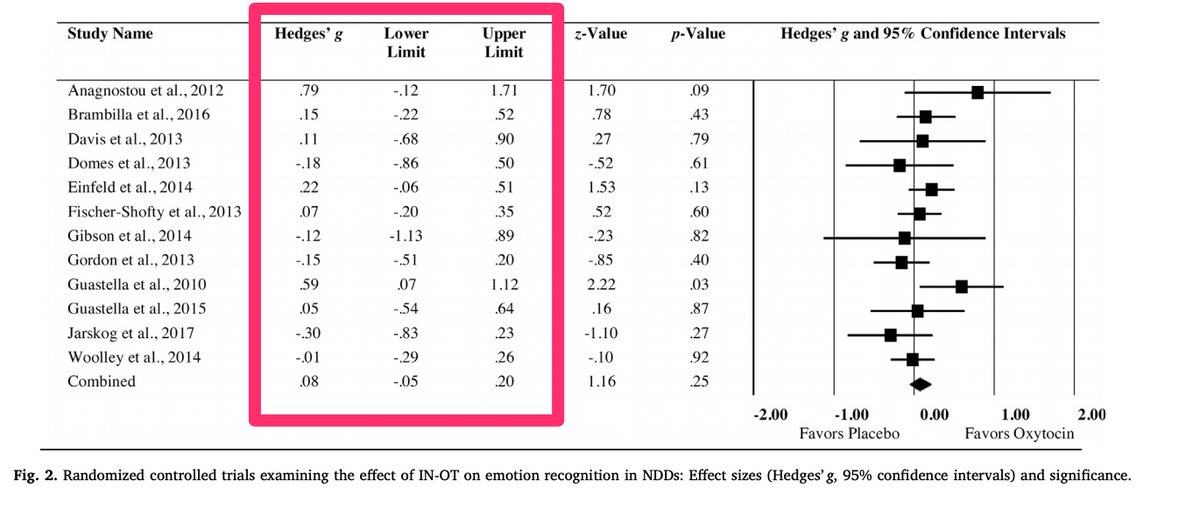
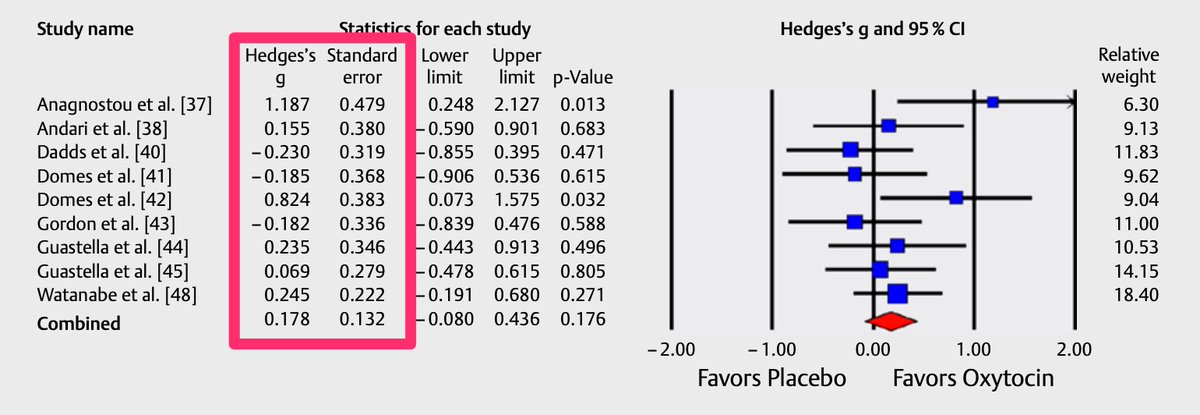
For first example, we& #39;re going to extract some data from this forest plot published in this meta-analysis on the impact of intranasal oxytocin on social cognition https://pubmed.ncbi.nlm.nih.gov/29032324/ ">https://pubmed.ncbi.nlm.nih.gov/29032324/...
All we need is the effect sizes and confidence interval info for each study
All we need is the effect sizes and confidence interval info for each study
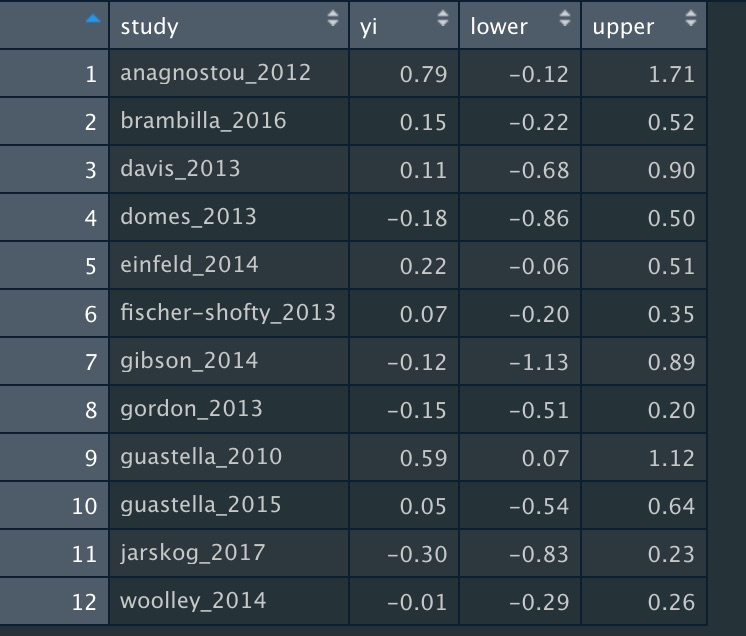
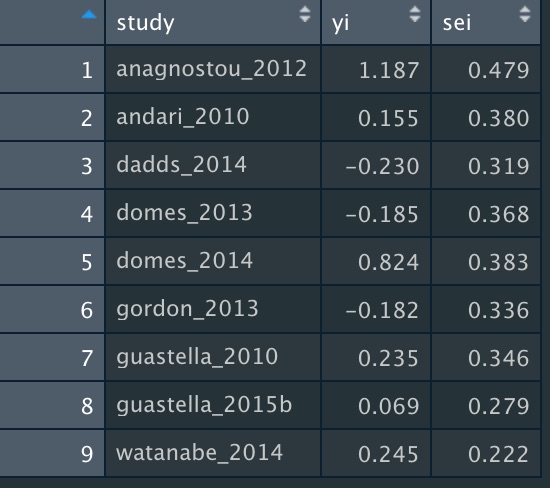
At a minimum, the dataset for analysis needs three columns, with the following labels:
1. "yi" for the effect size
2. "lower" for the lower CI bound
3. "upper" for the upper CI bound
You can also add a column for the study name, but this isn& #39;t strictly necessary
1. "yi" for the effect size
2. "lower" for the lower CI bound
3. "upper" for the upper CI bound
You can also add a column for the study name, but this isn& #39;t strictly necessary
Assuming we& #39;ve named this dataset "dat_keech", we& #39;re going to use this in the & #39;mapower_ul& #39; function. This requires three arguments:
1. The data
2. The observed summary effect size estimate
3 The name of the meta-analysis (required for the other core function we& #39;ll get to soon)
1. The data
2. The observed summary effect size estimate
3 The name of the meta-analysis (required for the other core function we& #39;ll get to soon)
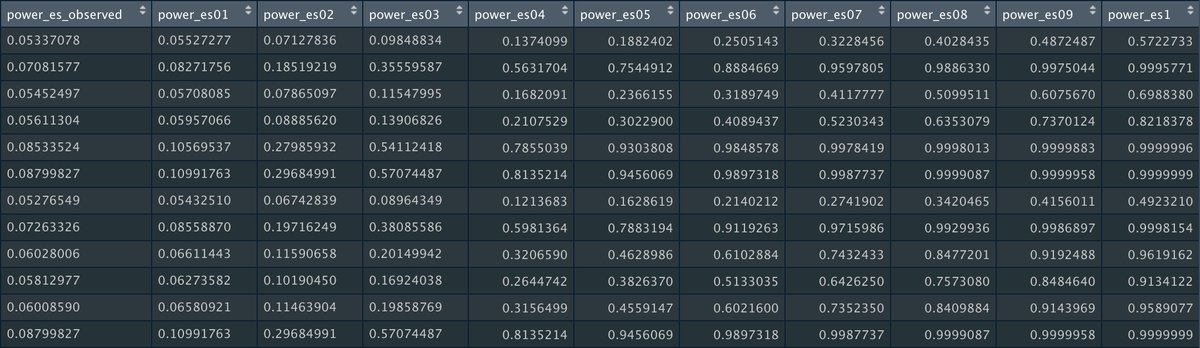
This will give us statistical power for a range of possible "true" effect sizes. The reported summary effect size ("power_es_observed") and a range of effect sizes from 0.1 to 1 (in increments on 0.1)
In this particular field, the average effect size is around 0.2, and that& #39;s probably inflated due to publication bias. So conservatively assuming that 0.2 is the true effect size, power ranges from 7% to 30% in these studies.
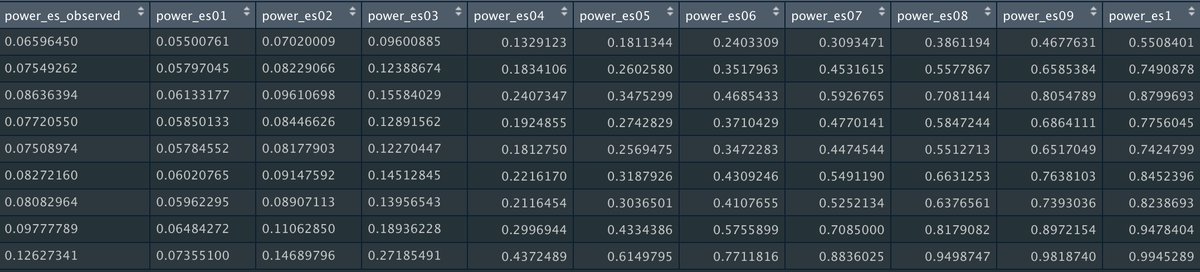
There& #39;s also a function for meta-analyses that report effect sizes and standard errors. To illustrate, let& #39;s extract the data from this forest plot published in this meta-analysis
For this function, only two columns are required
1. "yi" for the effect size
2. "sei" for the standard error
1. "yi" for the effect size
2. "sei" for the standard error
Assuming we& #39;ve named this dataset "dat_ooi", we& #39;re going to use this in the & #39;mapower_se& #39; function. This requires three arguments, as before
1. The data
2. The observed summary effect size estimate
3 The name of the meta-analysis
1. The data
2. The observed summary effect size estimate
3 The name of the meta-analysis
Sometimes it’s useful to calculate power for a body of meta-analyses, which might be reported in the same article or across articles. But Illustrating the power of individual studies from multiple meta-analyses can be difficult to interpret if there are many studies
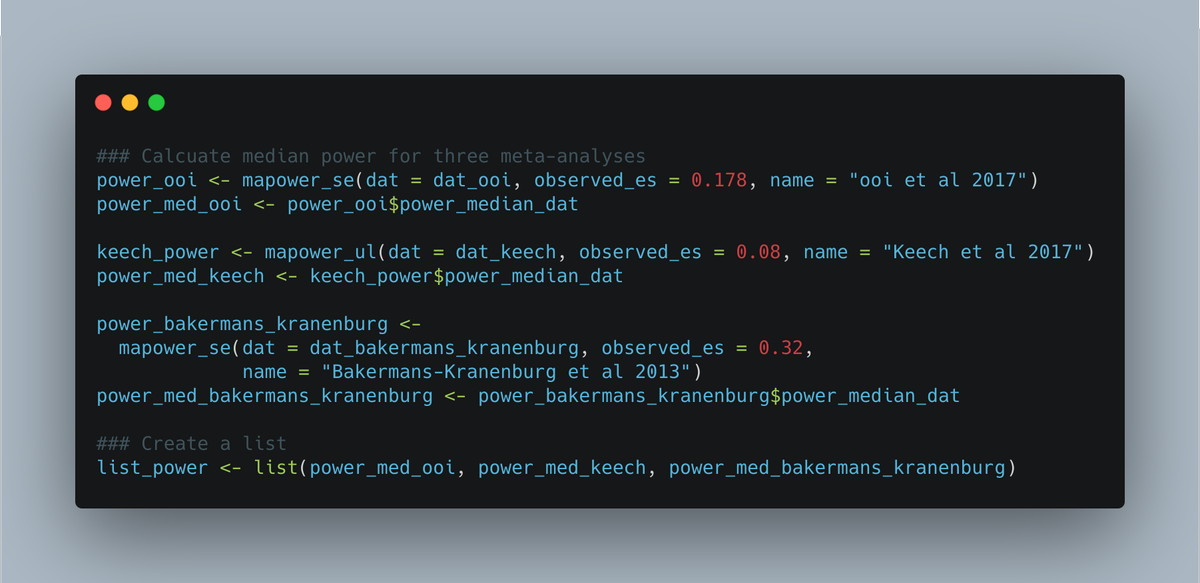
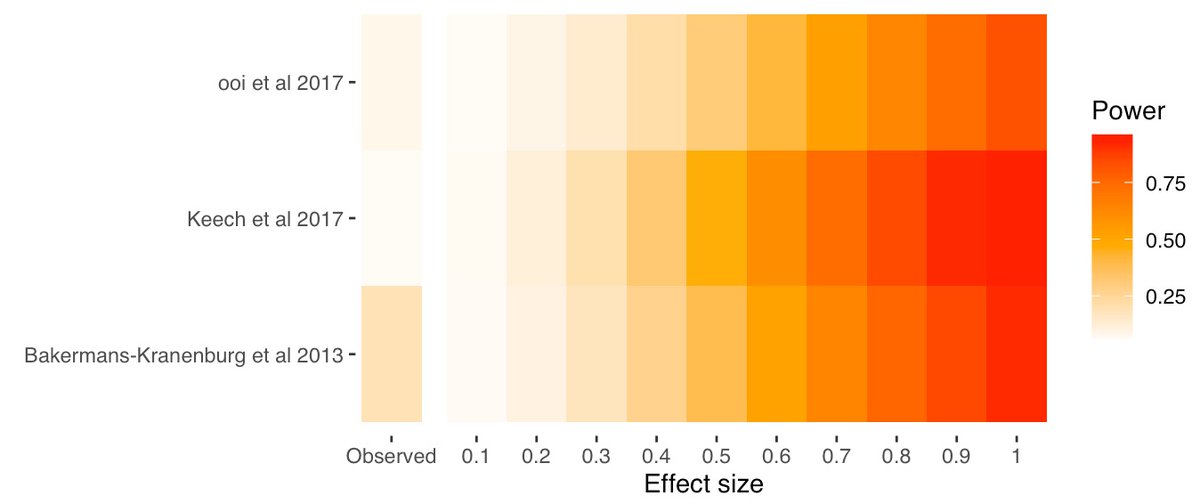
An alternative is to illustrate the power per meta-analysis by calculating the median power across studies. We can illustrate this with a “Firepower” plot, which we can create using the & #39;firepower& #39; function. First, we need to prepare the data. Here, we& #39;re combining three MAs
Now we& #39;re doing to create the firepower plot using the list we just created
Here& #39;s our Firepower plot  https://abs.twimg.com/emoji/v2/... draggable="false" alt="🎉" title="Partyknaller" aria-label="Emoji: Partyknaller">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🎉" title="Partyknaller" aria-label="Emoji: Partyknaller">
The blogpost version of this thread https://www.dsquintana.blog/metameta-r-package-meta-analysis/">https://www.dsquintana.blog/metameta-...

 Read on Twitter
Read on Twitter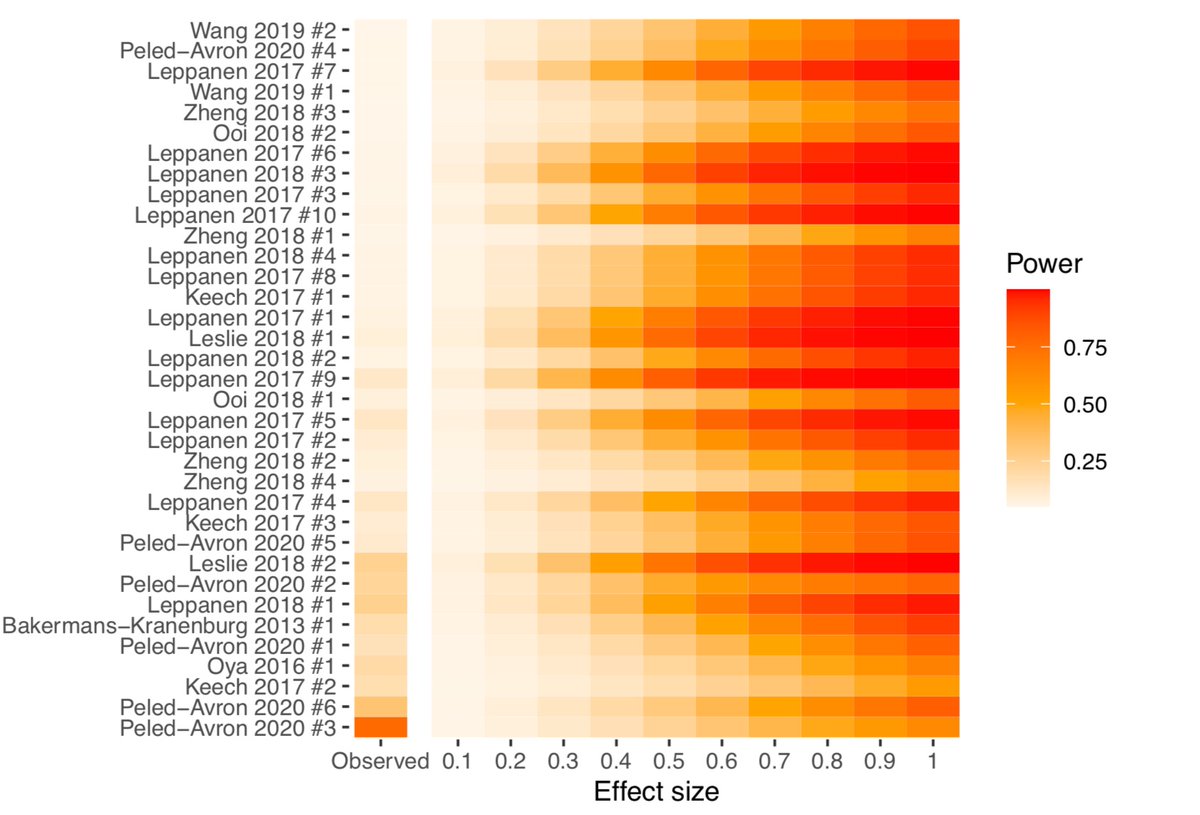 Here& #39;s a quick rundown on how you can use the {metameta} package to effortlessly calculate the statistical power of published meta-analyses to better understand the evidential value of included studies https://github.com/dsquintan..." title="I just released my first #Rstats package https://abs.twimg.com/emoji/v2/... draggable="false" alt="📦" title="Paket" aria-label="Emoji: Paket">Here& #39;s a quick rundown on how you can use the {metameta} package to effortlessly calculate the statistical power of published meta-analyses to better understand the evidential value of included studies https://github.com/dsquintan..." class="img-responsive" style="max-width:100%;"/>
Here& #39;s a quick rundown on how you can use the {metameta} package to effortlessly calculate the statistical power of published meta-analyses to better understand the evidential value of included studies https://github.com/dsquintan..." title="I just released my first #Rstats package https://abs.twimg.com/emoji/v2/... draggable="false" alt="📦" title="Paket" aria-label="Emoji: Paket">Here& #39;s a quick rundown on how you can use the {metameta} package to effortlessly calculate the statistical power of published meta-analyses to better understand the evidential value of included studies https://github.com/dsquintan..." class="img-responsive" style="max-width:100%;"/>



 " title="Here& #39;s our Firepower plot https://abs.twimg.com/emoji/v2/... draggable="false" alt="🎉" title="Partyknaller" aria-label="Emoji: Partyknaller">" class="img-responsive" style="max-width:100%;"/>
" title="Here& #39;s our Firepower plot https://abs.twimg.com/emoji/v2/... draggable="false" alt="🎉" title="Partyknaller" aria-label="Emoji: Partyknaller">" class="img-responsive" style="max-width:100%;"/>


