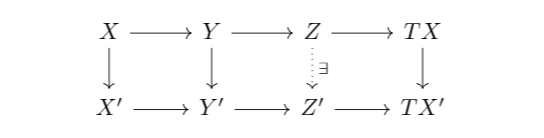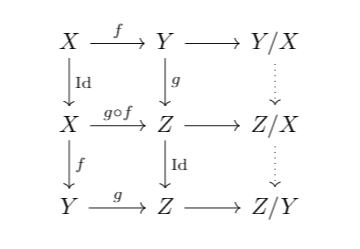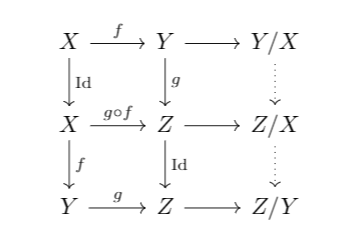triangulated categories

the audience of this thread is people who have some familiarity w/ category theory and homological algebra. i wish i could start from scratch but that would make this waay longer. c'est la vie.

some familiarity with algebraic topology/algebraic geometry would also be helpful for motivation, but not strictly necessary.

§0 definitions

first i need to talk about additive categories.
let C be a category.
an object x is initial if there is exactly one morphism from x to any other object in C.
x is terminal if there is exactly one morphism *to* x from any other category.

x is a zero object if it is both initial and terminal. the reason we call this a zero object is because in, say, abelian groups, the trivial group fits this bill. there's one morphism from 0 to any group, and from any group to 0.

next, direct sums. @Category_Fury did a really great thread on limits the other day, in it she mentions how you can take a limit of a 'discrete' diagram to get a product, and a colimit to get a coproduct. a direct sum is when these two things coincide https://twitter.com/Category_Fury/status/1279168272693248000?s=20

so if X and Y are objects, the direct sum (usually denoted with a circled + but i can't do that on twitter) X+Y acts as both a product and a coproduct. again, for an example look to abelian groups!

(btw there's a way of thinking of an initial object as a limit, if you take it over the empty diagram! with no objects in it and no morphisms!)

something to notice at this point: suppose C has a zero object. then between any two objects X and Y there is a distinguished morphism: the one which filters through the zero object. explicitly,
X-->0-->Y

C is an additive category if
1) it has a zero object,
2) it has all *finite* direct sums, and
3) the set Hom(X,Y) has the structure of an abelian group, such that composition distributes over the group operation.

the identity element of any Hom(X,Y) is going to be the "zero" morphism i mentioned earlier; that's going to come up later.

the idea of an additive category is that you can "add" objects together, and also morphisms.

finally, a functor F: C-->D between additive categories is itself additive if, as one would guess, it preserves the additive structure. so if X and Y are objects in C, then F(X+Y)=F(X)+F(Y), and the map
Hom(X,Y)-->Hom(F(X),F(Y)) is a group homomorphism.

now, let's talk about triangles. from here on out let C be an additive category, and let T:C-->C be an additive autoequivalence of C.

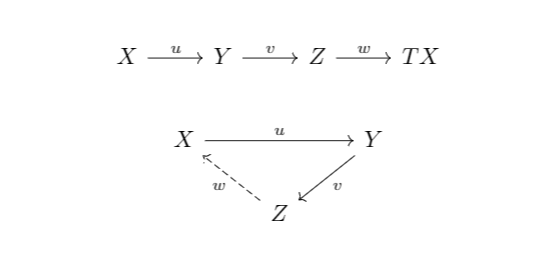
a triangle is a diagram of the form
X-->Y-->Z-->T(X)

the reason this is called a triangle is because you can arrange it in the following way, where w is dashed because it's not strictly a map between Z and X (and so this diagram is not a commutative one!!)

ok now we're (finally) ready to define triangulated categories!!

let C be an additive category, equipped with an additive self-equivalence T and a specified collection of triangles in C. that is to say, we don't care about *all* diagrams of this form, but a certain set of them.

we say C is triangulated if it satisfies the following axioms:

WAIT first let's say a triangle is *distinguished* if it lives in our specified collection.

TR1) talks about what kinds of triangles are distinguished.
first, any triangle of the form
X-->X-->0-->T(X)
is distinguished, where the map X-->X is the identity, and 0 is a zero object.

next, any triangle isomorphic to a distinguished triangle is also distinguished.

finally, any morphism X-->Y can be completed to some distinguished triangle X-->Y-->Z-->T(X)

this was just the first axiom y'all. i know this has been really heavy on exposition but we'll get to some fun stuff soon

TR2) is sometimes called the rotation axiom. it says that a triangle
X-->Y-->Z-->T(X)
is distinguished if and only if
Y-->Z-->T(X)-->T(Y)
is.

if you take the picture i put above where the triangle winds back on itself, you can imagine rotating that diagram to get a new triangle. the best picture for this is a helix, which is why @sarah_zrf has mentioned they should maybe be called helical categories.

ok next is TR3) which is best explained in the figure below: if you have a commutative square involving X, X', Y, and Y', you can first complete each row into a distinguished triangle, and then complete the entire diagram into a morphism of distinguished triangles.

if you've kept up so far you deserve a break. enjoy this meme

yeah so the simplest example i can give would probably be the homotopy category of chain complexes of modules over a commutative ring https://twitter.com/knotbrendan/status/1279480266667331586?s=19

in this case T is the translation functor which takes the item in degree 0 and shifts it to degree 1. (this is why it's called T btw)
for a morphism f:X-->Y you can construct what's called the mapping cone, which looks like Y+(T(X)), with a special differential depending on f

then you have triangles of the form
X-->Y-->Y+(T(X))-->T(X)
where morphism from Y is the inclusion (direct sum being a coproduct), and the morphism to T(X) is projection (direct sum being a product).

WAIT i thought of a somewhat simpler example: Z-graded vector spaces! it's exactly the same as the example above but you don't have to think about differentials.

ok so there's still one axiom to go! the dreaded octahedral axiom. half the books i own which talk about triangulated categories just skip this one but i wanna talk about it

first i wanna say that i hate the name octahedral axiom because it gives no intuition as to what's going on, it just notes that you can arrange the data into an octahedron. not helpful!

ok so let's go all the way back to group theory. there are four fundamental homomorphism theorems. i want to remind you of the third.
suppose A<B<C are nested groups, where A is normal in B, B is normal in C, and A is also normal in C.

then you can take quotients B/A, C/A, and C/B. moreover, you have a natural inclusion B/A into C/A, and the third homomorphism theorem says that (C/A)/(B/A) is isomorphic to C/B. "the denominators cancel"

if you want you can think of completing a morphism to a distinguished triangle as taking a quotient of sorts. it's not *quite* the same thing, cf the examples i gave above, but close enough!

one difference is that with groups you need a special type of morphism (normal inclusion) to get a quotient, but in a triangulated category you can start with any pair of composable morphisms. so let's do that! let
f:X-->Y and g:Y-->Z
be two morphisms.

there's a lot we get for free! consider the following diagram. we start with the first two columns. by TR1 we can complete each horizontal morphism to a distinguished triangle (i've suppressed some of the notation to make it easier to read)

by TR3 we get the dotted vertical arrows. what TR4 says is that the leftmost column forms a distinguished triangle. ie you can think of Z/Y as the quotient of Z/X by Y/X, which is basically the third homomorphism theorem!

ok to recap.
C is an additive category. T is an additive self-equivalence. we have a collection of distinguished triangles, satisfying some axioms.

TR1 tells you what kind of triangles are distinguished.
TR2 tells you that you can rotate triangles.
TR3 tells you how morphisms between triangles work.
TR4 gives you some control over triangles similar to other algebraic objects.

i was gonna do more but i'm pooped. i will continue this in the future, though. feel free to ask questions!