Récemment, un certain directeur d'un certain IHU disait ceci quand à la significativité des résultats d'un test clinique. En fait c'est contre-intuitif, mais c'est littéralement l'inverse.

Et niveau contre-intuitif, il y a plein de choses un peu contre-intuitives en stats, plein d'idées reçues auxquelles j'ai moi-même longtemps crues, donc même si je pense que ça a déjà été abordé des dizaines de fois, un rappel n'est peut-être pas inutile.

Donc on va parler biostatistiques, pvalues et significativité, entre autres. Et on finira par voir pourquoi la plupart des découvertes scientifiques publiées sont fausses (c'est suffisamment putaclic c'est bon ?)

Je vais commencer par préciser par rapport a la citation plus haut que par significativité on peut comprendre la significativité statistique, mais aussi la significativité biologique (c’est-à-dire, à quel point les résultats sont pertinents et ont du sens au niveau biologique).

Si un effet statistiquement significatif n'est pas forcément biologiquement significatif, un effet biologiquement significatif doit nécessairement être statistiquement significatif (s'il ne l'est pas, c'est qu'il n'y a pas d'effet), les deux notions sont donc liées.

On va d'abord parler de la significativité statistique du coup. Je vais considérer que vous savez ce qu'est un test statistique et une p-value parce que ça prendrait énormément de temps à vulgariser ici.

Si ce n'est pas le cas je vous recommande chaudement la chaîne de @ChatSceptique et cette vidéo de son ancienne chaîne youtube, ainsi que la chaîne de @RisqueAlpha

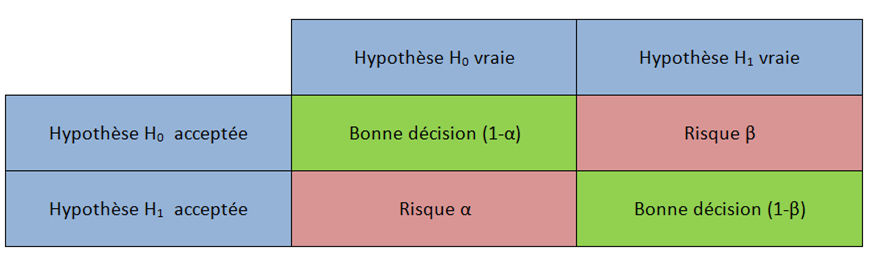
Par convention, on prend généralement 5% comme le seuil à partir duquel on considère que la p-value est significative. Mais la p-value étant la probabilité que nos données puissent être produites sous H0, on aura quand même 5% de chance que nos données soient compatibles avec H0.

Ce risque de se tromper, et d'accepter H1 alors que H0 est vraie, on l'appelle l'erreur de type 1, ou alpha. Cela implique vous vous en doutez une erreur de type 2, beta, le risque d'accepter H0 alors que H1 est vraie.

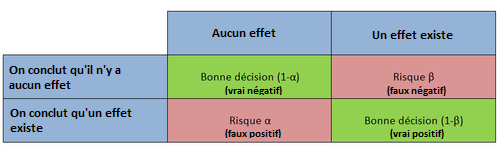
De manière plus vulgarisée, le risque alpha est le risque de conclure qu'on a un effet de ce que l'on teste, alors qu'il n'y en a pas réellement. C'est un faux positif. Le risque beta à l'inverse est le risque de manquer un effet en concluant qu'il n'existe pas, un faux négatif.

Une première idée reçue, que j'ai moi-même crue pendant longtemps, c'est qu'un faible échantillon augmente le risque de faux positif, donc le risque alpha. C'est quelque chose que je dis notamment dans ma vidéo sur Séralini.

En réalité, le risque alpha est 𝗶𝗻𝗱𝗲́𝗽𝗲𝗻𝗱𝗮𝗻𝘁 𝗱𝗲 𝗹𝗮 𝘁𝗮𝗶𝗹𝗹𝗲 𝗱'𝗲́𝗰𝗵𝗮𝗻𝘁𝗶𝗹𝗹𝗼𝗻 et ne dépend que du seuil que l'on fixe. Si on fixe un seuil de 5%, alors le risque de faux positifs est de 5%.

Ce que je dis dans ma vidéo sur Séralini, c'est qu'avec un faible échantillon, on a plus de risques d'avoir des valeur extrêmes, et la moyenne de nos valeurs sera affectée.

Pour illustrer cela, j'utilise des lancers de dés. Lancez un dé une fois, votre moyenne sera constituée d'un seul point : 1, 2, 3, 4, 5, ou 6. Lancez le une deuxième fois et il aura plus de chances de se rapprocher du "milieu", 3,5.

Plus vous lancerez le dé, plus votre moyenne se rapprochera de 3,5. En lançant le dé très peu de fois, vous pourriez conclure sur une moyenne de 2, 5 ou 6 par exemple, et vous dire que votre dé est pipé, alors que c'est faux, donc un faux positif.

Pourquoi alors est-ce que le risque alpha n'est-il pas augmenté ? On va quitter les lancers de dés et revenir à Séralini. On va comparer un groupe recevant du RoundUp, et un groupe n'en recevant pas. Et pour observer l'effet on va compter la masse des tumeurs qui se développent.

Je vais inventer des chiffres pour illustrer, évidemment cela ne représentera pas la réalité ni les chiffres de Séralini. Pour cela j'ai fait des simulations sur le logiciel R. Je peux vous donner le script que j'ai utilisé si ça vous intéresse.

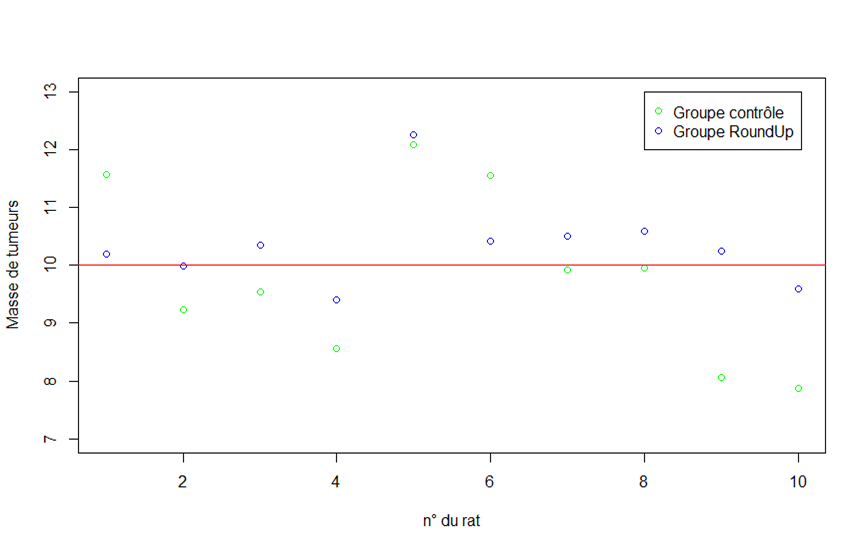
Disons qu'en moyenne, un rat Sprague Dawley développe 10g de tumeurs au cours de sa vie. Je simule cela pour un groupe de 10 rats, et j'obtiens ces masses de tumeurs pour chacun de mes rats :

Maintenant je fais la même chose pour mon second groupe de 10 rats, en considérant ici qu'il n'y a pas d'effet du RoundUp (donc même moyenne, j'utilise la même commande sur R), j'obtiens ceci.

Représenté graphiquement j'ai cette distribution, plutôt centrée autour de 10g, avec un peu de variabilité.

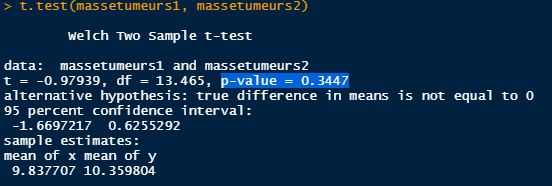
Pour déterminer si les deux groupes sont différents statistiquement, je fais un test de Student, et j'obtiens une p-value de 0,34, soit 34%, donc non significative.

Mais là j'ai fait ce test une seule fois. On a dit que par chance on pouvait tomber sur des valeurs extrêmes, j'ai peut-être pas eu de chance.

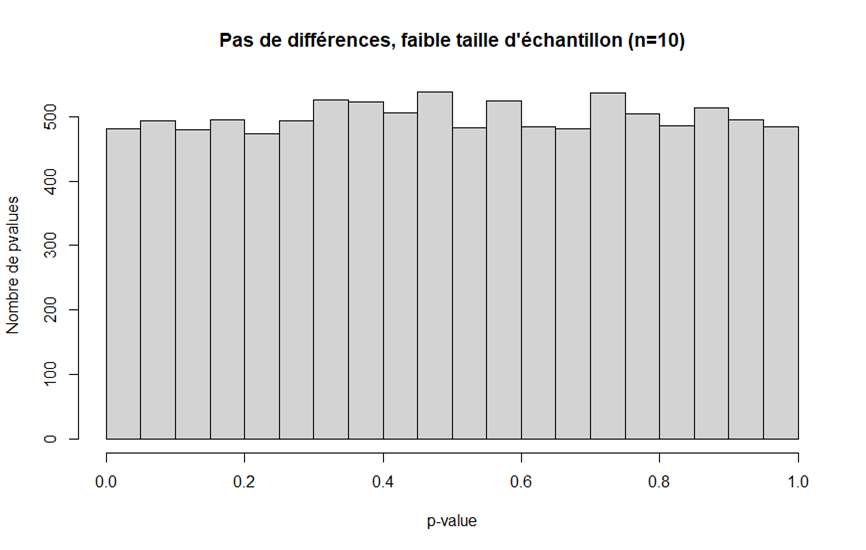
Du coup, on va simuler cette procédure 𝗗𝗜𝗫 𝗠𝗜𝗟𝗟𝗘 fois, et voir les p-values qu'on obtient. La distribution des p-values que l'on obtient est en fait très uniforme. On a autant de chances d'avoir une p-value faible qu'une p-value élevée.

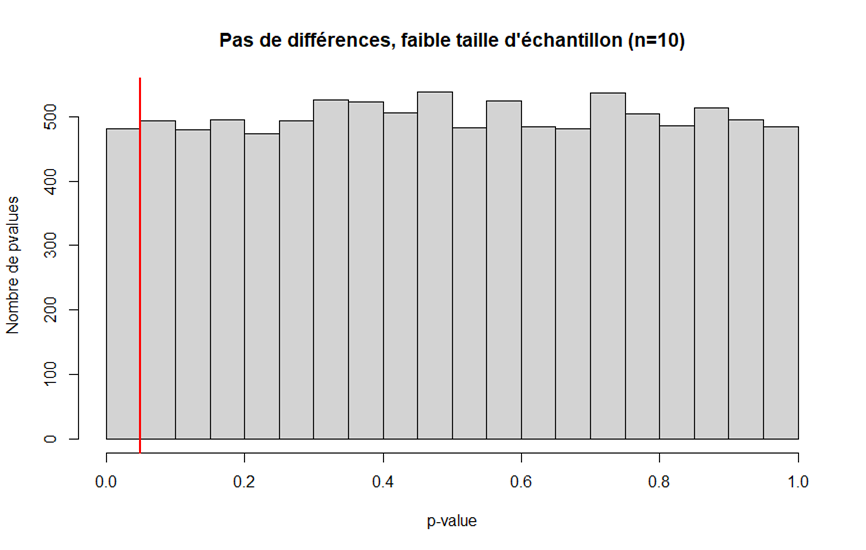
En mettant un seuil à 0.05, on voit qu'environ 5% du temps, on aura une p-value significative. Soit exactement notre seuil. Cela confirme bien que notre risque alpha ne dépend que de ce seuil.

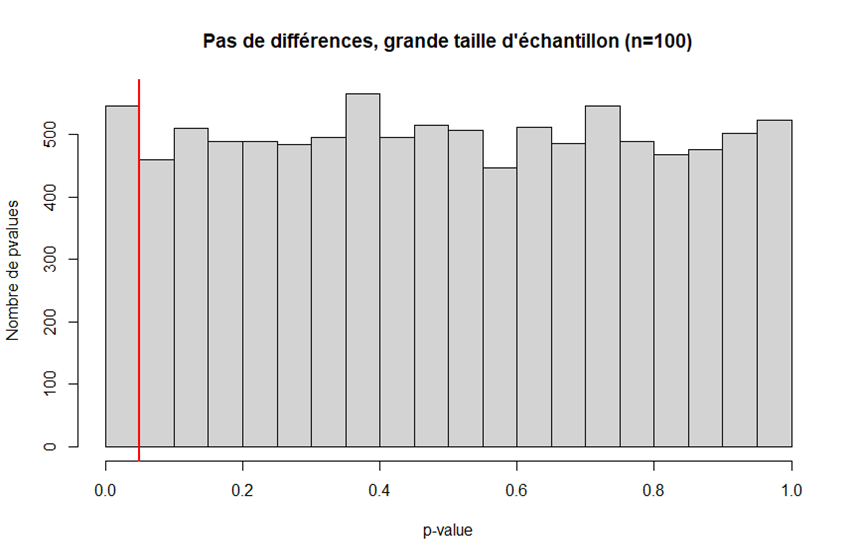
Maintenant regardons ce que l'on obtient en augmentant la taille de l'échantillon. Avec n=100, on a un résultat similaire. Cela confirme encore une fois que le risque alpha dépend du seuil, et pas de la taille de l'échantillon.

Mais alors comment Séralini a-t-il pu conclure dans son étude à des effets du RoundUp ? La réponse est simple : il n'a tout simplement pas fait de test statistique. Eh oui, tu peux pas avoir de p-value non significative si tu ne fais pas les tests.

Le Haut Conseil des Biotechnologies avait repris l'étude en faisant les stats, et n'avait effectivement pas trouvé de résultat statistiquement significatif.
http://www.hautconseildesbiotechnologies.fr/sites/www.hautconseildesbiotechnologies.fr/files/file_fields/2015/06/30/121019etudeseraliniaviscshcb.pdf

Bon je pense qu'on a fait le tour du risque alpha, quid du risque beta maintenant ?

Cette fois je simule des jeux de données avec des moyennes différentes, d'abord de 10% (première ligne), puis de 100% (seconde ligne) le reste de la procédure reste la même.
En vert, la bonne décision, en rouge, les faux négatifs (beta).

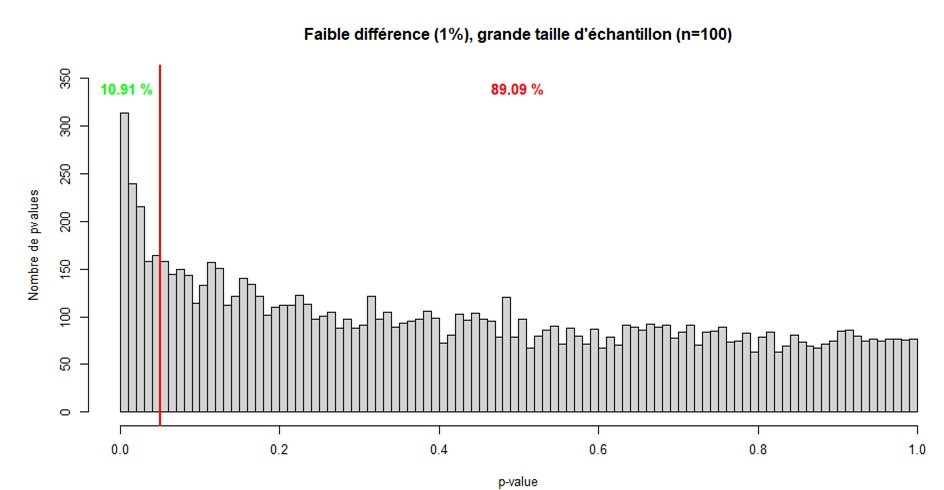
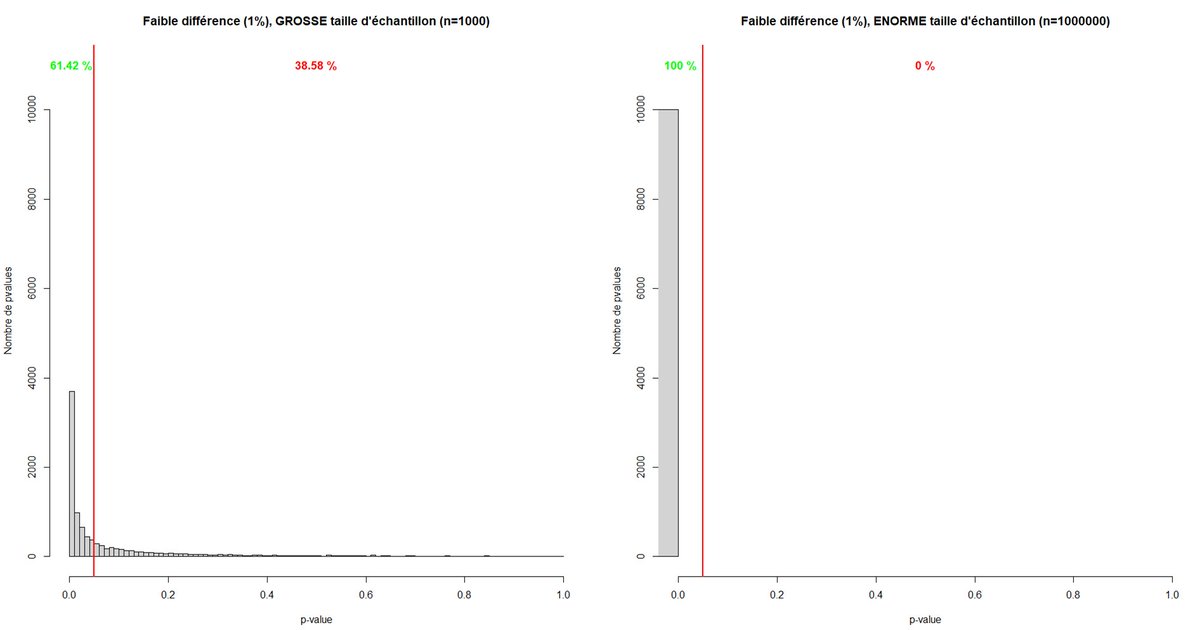
Pour une faible différence, avec un petit échantillon on observe une distribution similaire aux distributions précédentes. Sauf qu'ici, le bon choix est quand on a une p-value significative. Ici le risque beta est énorme. 95% du temps, on se trompera.

En augmentant la taille de l'échantillon, on voit que la distribution change grandement. Ici, on voit bien que le risque beta est diminué, on ne se trompera que 90% du temps.

Cela reste énorme, mais en augmentant encore la taille de l'échantillon (certaines études de grande envergure pouvant aller jusqu'à des tailles de l'ordre du million), le risque beta diminue voire devient nul.

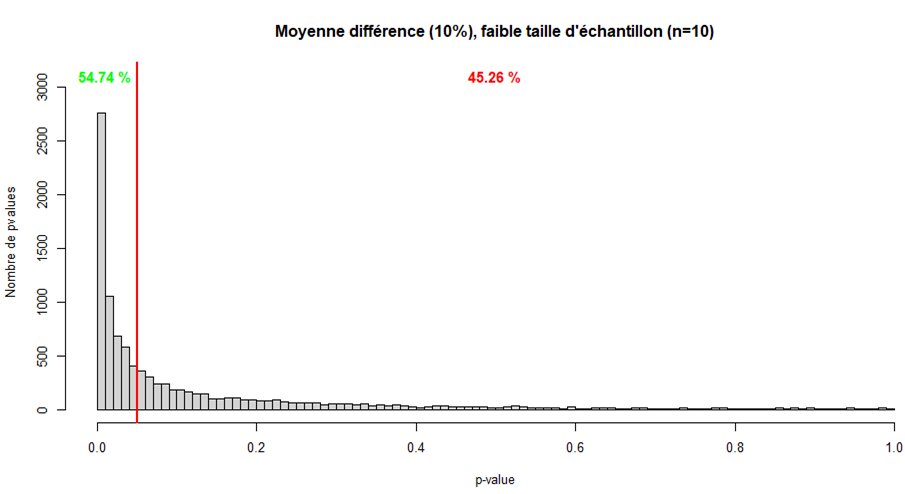
Mais trouver une différence si faible est pas forcément intéressant (biologiquement significatif), on sera plus intéressés par des effets plus grands. Avec un effet de 10%, même un faible échantillon est capable de trouver une p-value significative environ 55% du temps ici.

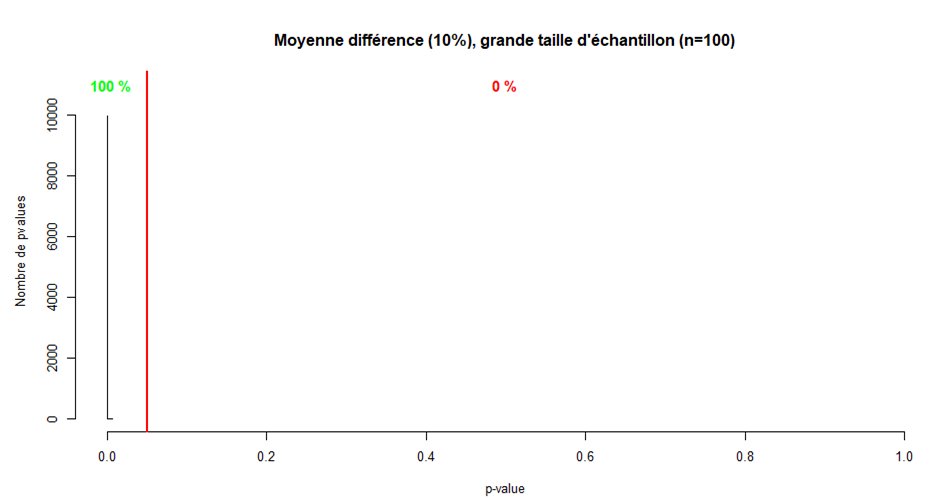
Mais on se trompera tout de même quasiment une fois sur deux. Avec un échantillon plus grand, pas forcément énorme, on ne se trompe déjà plus jamais ici.

Après avoir rédigé ce thread je vois que @T_Fiolet aborde cela ici aujourd'hui, parce qu'apparemment Peronne en a rajouté une couche, donc je vous conseille d'aller lire ça, vu qu'il aborde aussi les notions dont je parle. https://mobile.twitter.com/T_Fiolet/status/1272938528712921088

Ces exemples montrent que là où la taille de l'échantillon est cruciale, c'est pour diminuer le risque beta, et non le risque alpha.

Si avec un très grand échantillon (et peu importe la taille de l'échantillon en fait) vous obtenez un résultat significatif, vous ne pourrez pas savoir s'il s'agit d'un vrai positif ou d'un faux positif.

Le seul moyen de s'assurer que votre résultat est un vrai positif est que ce résultat soit répliqué, idéalement indépendamment, car il est bien moins probable d'avoir un faux positif plusieurs fois de suite.

Malheureusement à l'heure actuelle, on observe plutôt l'inverse, et de nombreux biais font que le risque alpha est en réalité bien plus important.

Premièrement, les journaux scientifiques ont tendance à ne pas accepter les réplications d'études existantes, on préfère les résultats innovants, et il est donc difficile de pouvoir confirmer si les résultats significatifs publiés sont des vrais positifs ou pas.

Deuxièmement, les journaux scientifiques, encore eux, ont aussi tendance à ne pas accepter des résultats non significatifs.

Sur mes exemples de 10000 simulations, 500 seront acceptées, et 9500 refusées (bon c'est caricatural mais vous avez l'idée). On se retrouve donc avec 500 résultats positifs, on en conclura à l'existence d'un effet, alors que cet effet n'existe pas réellement.

Ça, ça s'appelle le biais de publication, et ça fait que l'on va retrouver beaucoup plus de faux positifs que l'on devrait.

Une des pratiques pour éviter cela consiste à valider le protocole en amont, et garantir la publication par le journal sur la base de la méthode et non des résultats. Malheureusement c'est une pratique peu répandue aujourd'hui.

Un autre biais qui intervient, c'est le p-hacking. Comme j'ai dit, les journaux aiment bien les p-values significatives, et les chercheurs aussi. Malheureusement, ils vont avoir tendance à faire en sorte que leur p-value soit significative, que l'effet soit réel ou non.

Par exemple, comme illustré sur ce strip de xkcd, on peut segmenter notre analyse, et au lieu de chercher un effet de bonbons, on va regarder si les bonbons de telle couleur ont un effet. Comme on a 5% de risque de faux positif, on aura un faux positif une fois sur 20 en moyenne

La probabilité de tomber au moins une fois sur un faux positif suit la formule p= 1-(1-alpha)^n, avec n le nombre de tests que l'on fait. Avec alpha = 5%, on a donc p=1-0,95^n. On voit ainsi qu'en faisant deux tests on a 9,75% de probabilités d'avoir au moins un faux positif.

En faisant 20 tests différents, on est déjà à 64% de probabilité. Pour 30 tests, 78%. Bref, plus on fait de tests, plus on augmente nos risques d'avoir un faux positif.

Mais pourtant ça peut être intéressant de chercher si la couleur des bonbons a un impact. Peut-être qu'un colorant particulier aura un effet. Comment faire alors ?

Pour éviter cela, il existe des procédures de correction de la p-value. La plus simple et la plus fréquente est la correction de Bonferroni qui consiste à diviser notre seuil par le nombre de tests que l'on fait.

En faisant 20 tests, il ne faudra plus une p-value de 0,05, mais une p-value de 0,05/20 = 0,0025, soit 0,25%, pour que l'on considère notre résultat comme significatif. Ces corrections permettent ainsi de diminuer notre risque alpha.

Malheureusement, tous les chercheurs n'utilisent pas ces corrections, et beaucoup d'articles sans ces corrections sont publiés, ce qui fait que notre risque alpha reste assez grand.

Une autre pratique de p-hacking, c'est d'ajouter ou retirer des valeurs à nos jeux de données, et refaire un test à chaque fois, jusqu'à ce qu'on tombe sur une p-value significative.

Concrètement, ça revient à piocher plusieurs fois une p-value jusqu'à tomber sur une sous les 5%, et ignorer toutes celles qui tombent sur la droite de la ligne rouge

Et attention, je ne dis pas que les chercheurs qui font cela sont malintentionnés, en fait beaucoup de chercheurs font cela sans même s'en rendre compte, avec toutes les bonnes intentions du monde. Et ils trouvent même des justifications parfaitement sensées pour cela.

Il y a d'autres pratiques de p-hacking mais vous voyez l'idée. Le résultat est qu'on a bien plus de faux positifs qui se trouvent publiés qu'il ne devrait.

Le tout est aussi accentué par des chercheurs qui ne maîtrisent pas les stats et font leurs tests n'importe comment.

Et le peer review n'aide pas vraiment sur cela car les reviewers font aussi partie des chercheurs du domaine, et ne maîtrisent pas forcément les stats non plus.

(et bon je parle pas des cas ou ya carrément pas de peer review, ou qu'il est totalement baclé)

Concernant le risque beta, le problème c'est qu'énormément d'études sont à faible envergure, la recherche manquant beaucoup de moyens, donc avec un risque beta très grand. Beaucoup de ces études finiront négatives, probablement même non publiées à cause de ces résultats négatifs.

Donc d'un côté on a beaucoup trop de faux positifs, de l'autre très peu de vrais positifs.
C'est ce qui a amené les chercheurs, notamment John Ioannidis, à dire que la plupart des résultats positifs publiés sont faux. https://journals.plos.org/plosmedicine/article?id=10.1371/journal.pmed.0020124

Avant de conclure je vais revenir sur la significativité biologique.
La taille d'échantillon n'influe en rien sur l'importance de l'effet, et vice versa.

Quand dans la première citation on lit "Avec 10.000 personnes, quand les différences sont faibles, parfois, elles n'existent pas", on peut comprendre qu'avec un si grand échantillon on détectera des effets minimes, peu biologiquement significatifs. C'est vrai.

Mais un résultat statistiquement significatif avec un petit échantillon peut être un grand effet, un petit effet (avec de la chance vu que le risque beta est grand) ou un faux positif.

A l'inverse avec un grand échantillon, on maximise nos chances de trouver un vrai positif, que l'effet soit grand ou non. Et c'est pas compliqué de regarder derrière si l'effet est important ou pas. Si pour un groupe on a une moyenne de 10, et pour l'autre 20, l'effet est clair.

En conclusion :
- le risque alpha ne dépend pas de la taille d'échantillon
- un grand échantillon permet de diminuer le risque beta et donc plus facilement déceler un effet réel

- pour minimiser ces risques, il faut des études de qualité, de grande envergure, avec le moins de biais possibles, il faut répliquer les études et publier les résultats négatifs

Du coup j'ai mis le script ici, j'ai essayé de l'annoter assez clairement mais je sais pas si ça le sera suffisamment https://drive.google.com/file/d/1-uYUyR4Bh99qQTE2z2292jNQu_emsRrp/view?usp=sharing