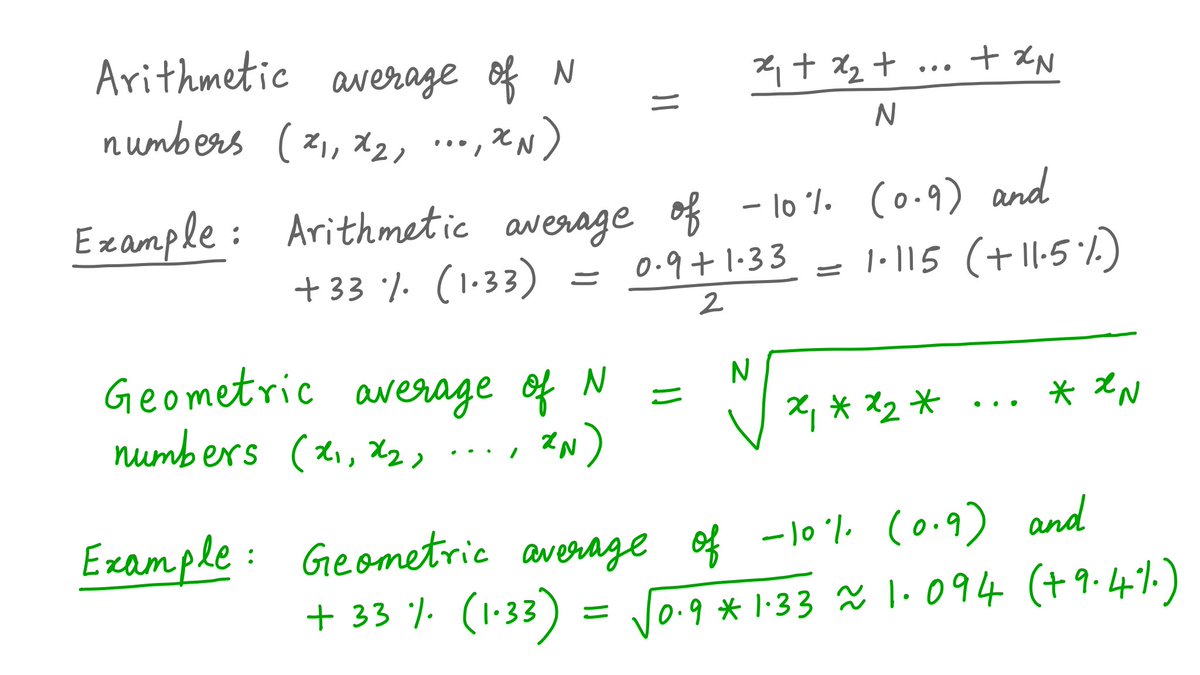1/
Get a cup of coffee.
In this thread, I& #39;ll show you why "geometric thinking" is superior to "arithmetic thinking" while making investment decisions.
Get a cup of coffee.
In this thread, I& #39;ll show you why "geometric thinking" is superior to "arithmetic thinking" while making investment decisions.
2/
Let& #39;s start with an example.
There are 2 stocks, A and B.
A goes up 10% every year. Like clockwork.
B is more volatile. Half the years, it goes down 10%. But the other half, it compensates by going up 33%.
Let& #39;s start with an example.
There are 2 stocks, A and B.
A goes up 10% every year. Like clockwork.
B is more volatile. Half the years, it goes down 10%. But the other half, it compensates by going up 33%.
3/
You have $10,000.
You have to pick a stock (A or B), put your entire $10K in it, and not touch it for 20 years.
Do you pick A or B?
You have $10,000.
You have to pick a stock (A or B), put your entire $10K in it, and not touch it for 20 years.
Do you pick A or B?
4/
Some mental math for Option B: half the years, B is down 10%. The other half, it& #39;s up 33%. On average, that& #39;s a 11.5% return, right? After all, (-10% + 33%)/2 = 11.5%.
That seems better than Option A& #39;s steady 10%.
So you should pick B over A, right?
Read on.
Some mental math for Option B: half the years, B is down 10%. The other half, it& #39;s up 33%. On average, that& #39;s a 11.5% return, right? After all, (-10% + 33%)/2 = 11.5%.
That seems better than Option A& #39;s steady 10%.
So you should pick B over A, right?
Read on.
5/
Say you choose Option B. You put your $10K in stock B. You hold for 20 years.
As advertised, B goes up 33% during 10 of those years, and down 10% during the other 10.
How much are you left with?
That& #39;s easy. You& #39;d have $10K*(0.9^10)*(1.33^10) = $60,387.
Not bad.
Say you choose Option B. You put your $10K in stock B. You hold for 20 years.
As advertised, B goes up 33% during 10 of those years, and down 10% during the other 10.
How much are you left with?
That& #39;s easy. You& #39;d have $10K*(0.9^10)*(1.33^10) = $60,387.
Not bad.
6/
If instead, you& #39;d been a sucker and taken Option A& #39;s steady 10%, how much would you have?
Even easier. $10K*(1.1^20) = $67,275.
Wait, Option A gets you $6,888 *more* than Option B?
How& #39;s that possible?
If instead, you& #39;d been a sucker and taken Option A& #39;s steady 10%, how much would you have?
Even easier. $10K*(1.1^20) = $67,275.
Wait, Option A gets you $6,888 *more* than Option B?
How& #39;s that possible?
7/
The reason is: "arithmetic thinking" vs "geometric thinking".
Let me explain. How did we calculate the average 11.5% return for Option B?
We just took the average of -10% and +33%. (-10% + 33%)/2 = +11.5%. That& #39;s "arithmetic".
The reason is: "arithmetic thinking" vs "geometric thinking".
Let me explain. How did we calculate the average 11.5% return for Option B?
We just took the average of -10% and +33%. (-10% + 33%)/2 = +11.5%. That& #39;s "arithmetic".
8/
But how did the $10K invested in B actually behave?
Half the years (-10%), it got multiplied by 0.9. And the other half (+33%), it got multiplied by 1.33.
That& #39;s a growth rate of ((0.9^10)*(1.33^10))^(1/20), or 9.4%. Not 11.5%.
But how did the $10K invested in B actually behave?
Half the years (-10%), it got multiplied by 0.9. And the other half (+33%), it got multiplied by 1.33.
That& #39;s a growth rate of ((0.9^10)*(1.33^10))^(1/20), or 9.4%. Not 11.5%.
9/
This 9.4% is the *geometric* average of -10% and +33%. The 11.5% was their *arithmetic* average.
To many people, average just means arithmetic average.
But if you make investment decisions all day long, you probably encounter geometric averages far more often.
This 9.4% is the *geometric* average of -10% and +33%. The 11.5% was their *arithmetic* average.
To many people, average just means arithmetic average.
But if you make investment decisions all day long, you probably encounter geometric averages far more often.
10/
Key lesson: Money does not grow arithmetically. It compounds geometrically.
So, when you make investment decisions, "geometric thinking" is superior to "arithmetic thinking".
Key lesson: Money does not grow arithmetically. It compounds geometrically.
So, when you make investment decisions, "geometric thinking" is superior to "arithmetic thinking".
12/
Here& #39;s an interesting mathematical fact:
The geometric average of any N positive numbers *never* exceeds their arithmetic average.
This is called the "Arithmetic Mean/Geometric Mean theorem", or the "AM/GM theorem" for short.
https://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means">https://en.wikipedia.org/wiki/Ineq...
Here& #39;s an interesting mathematical fact:
The geometric average of any N positive numbers *never* exceeds their arithmetic average.
This is called the "Arithmetic Mean/Geometric Mean theorem", or the "AM/GM theorem" for short.
https://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means">https://en.wikipedia.org/wiki/Ineq...
13/
You may have noticed that I said "positive numbers" in the theorem above.
But don& #39;t worry. When we work with money, our numbers are always positive. Even a negative 10% return is just multiplication by 0.9, a positive number.
So the theorem always applies.
You may have noticed that I said "positive numbers" in the theorem above.
But don& #39;t worry. When we work with money, our numbers are always positive. Even a negative 10% return is just multiplication by 0.9, a positive number.
So the theorem always applies.
14/
The AM/GM theorem means:
If you approximate annual returns by taking their arithmetic average, you will always *overestimate* your actual return.
So, arithmetic thinking is not just wrong. It& #39;s dangerous. It makes you think you& #39;ll have more money than you& #39;ll actually do.
The AM/GM theorem means:
If you approximate annual returns by taking their arithmetic average, you will always *overestimate* your actual return.
So, arithmetic thinking is not just wrong. It& #39;s dangerous. It makes you think you& #39;ll have more money than you& #39;ll actually do.
15/
Think about what this means for pension funds and 401-Ks that assume a steady 7% return.
If the fund loses money some years and makes it up in others, it may do worse than 7% long term.
And AM/GM *guarantees* it, if the average arithmetic annual return is 7%.
Think about what this means for pension funds and 401-Ks that assume a steady 7% return.
If the fund loses money some years and makes it up in others, it may do worse than 7% long term.
And AM/GM *guarantees* it, if the average arithmetic annual return is 7%.
16/
Humans are wired so that geometric thinking is much harder for most people than arithmetic thinking.
If you cultivate geometric thinking, you& #39;ll have an edge over most people.
Humans are wired so that geometric thinking is much harder for most people than arithmetic thinking.
If you cultivate geometric thinking, you& #39;ll have an edge over most people.
17/
Warren Buffett can do geometric calculations (square roots, cube roots, CAGRs) in his head.
To him, thinking geometrically is as effortless as thinking arithmetically is to us.
This is a huge edge.
https://twitter.com/BrentBeshore/status/1004444368680439808?s=20">https://twitter.com/BrentBesh...
Warren Buffett can do geometric calculations (square roots, cube roots, CAGRs) in his head.
To him, thinking geometrically is as effortless as thinking arithmetically is to us.
This is a huge edge.
https://twitter.com/BrentBeshore/status/1004444368680439808?s=20">https://twitter.com/BrentBesh...
18/
Yes, geometric calculations are hard.
And we& #39;re not Buffett. Most of us can& #39;t do geometric averages in our heads.
But we& #39;re surrounded by calculating machines. Smartphones. Tablets. Laptops. Excel. Python.
No excuse for not using them while taking important decisions.
Yes, geometric calculations are hard.
And we& #39;re not Buffett. Most of us can& #39;t do geometric averages in our heads.
But we& #39;re surrounded by calculating machines. Smartphones. Tablets. Laptops. Excel. Python.
No excuse for not using them while taking important decisions.
19/
Thanks for reading. Enjoy your weekend. Be safe. Think geometric. https://abs.twimg.com/emoji/v2/... draggable="false" alt="😀" title="Grinning face" aria-label="Emoji: Grinning face">
https://abs.twimg.com/emoji/v2/... draggable="false" alt="😀" title="Grinning face" aria-label="Emoji: Grinning face">
/End
Thanks for reading. Enjoy your weekend. Be safe. Think geometric.
/End

 Read on Twitter
Read on Twitter