Let's talk about a random #coding problem:

For a given array, count all subarrays that sum to a perfect square. (Count all (i,j) such that a_i + ... + a_j = k², for some k∈ℕ).

It's a fun lil problem: easy to ask, good for interviews, illustrates some tricks. (1/n)

Let's look at some examples. For an array [2,2,6] the answer is 1, as 2+2 gives you the only square (4).

For an array [4,0,0,9] however the answer is 9, as {[4], [4,0], [4,0,0], [0], [0,0], another [0], [0,0,9], [0,9] and [9]} all sum to a perfect square.

(The problem comes from Google Kickstart competition last Saturday:

https://codingcompetitions.withgoogle.com/kickstart/round/000000000019ff43/00000000003381cb

It now has an "Analysis" section, but I'm not a huge fan of how it's written, and also it's technically wrong for Python, so here's my version :)

Let's start with a stupid brute-force solution: consider all possible right borders (from 1 to n), and all left borders (from 0 to n-1), calculate each sum, check if it's a square. (The only cute point here is about not making the off-by-one error for the right border).

It totally works, but it's painfully slow (~30 s for one 1000-long sequence). j goes through n points; then for each j, i goes through ~n/2 points on average, then yet within it we sum(), going through ~n/3 points; it's O(n3) already! And sqrt() uses an inner loop with ~√n more.

What can we do? We can pre-calculate a bunch of square values, hash them, and check in a hash table instead of calculating a sqrt. It will kill this inner loop in sqrt() algorithm, but the improvement is marginal (from O(n3.5) to O(n3)). It's like 5% on a 1000-long array.

What else can be done? We can get rid of an implicit loop in sum(a[i:j]) by noticing that sum{i,j+1} = sum{i,j}+a[j+1] (and similarly sum{i+1,j} = sum{i,j}-a[i]). So if we arrange all subarrays in a clever sequence, moving-frame-style, we can instantly shift from O(n3) to O(n2).

This is a big help (~90% improvement for n=1000), but can we do better?

It turns out, there's a famous weird trick that allows to shave one more degree of n under O by replacing one loop with checks in a hash table. It doesn't make sense at first, but consider a simpler problem:

"Count all pairs of elements (not subarrays) that sum to a target value of S"
We can of course loop through all pairs of (i,j). But we can also loop through a_i once, putting S-a_i on a hashed "wanted list". Then check whether each new a_i is on this list.

How come it's faster? Why working with a hashed table of "wanted items" is faster than looking through an array of "available items"? Think of jigsaw puzzles. If you have one piece missing, you can match new pieces instantly, as spatial arrangement works kinda like hashing?

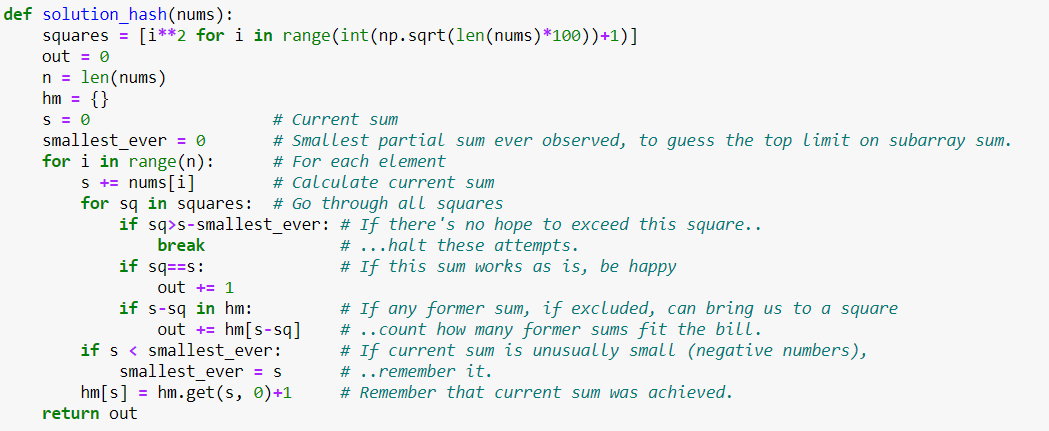
Either way, here's a solution for the original problem with a hash table. As with a hash table, we can only check one value at a time, we have to bring the loop over all perfect squares back into the game. But it's OK, as this loop is much shorter, and we can quit it early.

This solution gives a 99% improvement for n=1000, as now the complexity is O(n*something) (not sure what exactly, but better than O(n2).

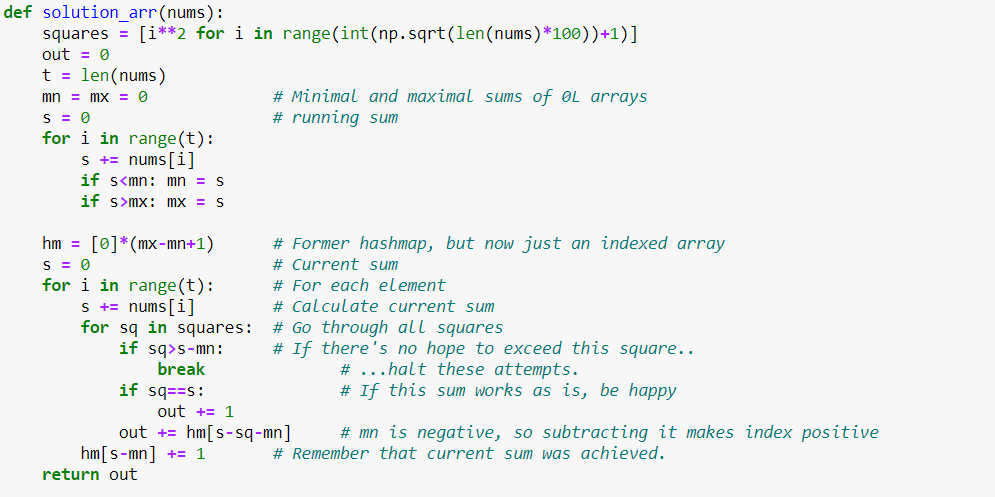
Can we do even better? The "Official answer" suggests that replacing a hash table with an ordered list (array) can help even further, but it didn't do anything for me. Perhaps Python is better with sets than with lists?

https://codingcompetitions.withgoogle.com/kickstart/round/000000000019ff43/00000000003381cb

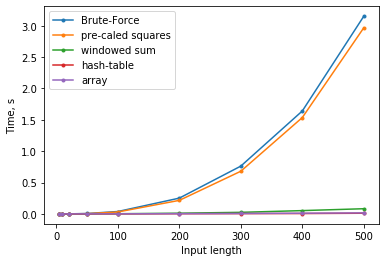
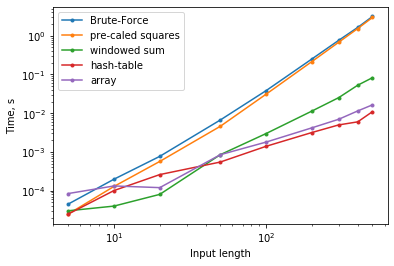
Finally, here are some performance tests for inputs of different length. The left plot (linear scale) makes you appreciate just how bad the brute-force solution is. The right one (log-scale) shows that windowed sum wins for small n, but hashed version wins for large n.

All code in this thread can be found here:

https://github.com/khakhalin/Sketches/blob/master/oldkickstart/2020c/3_perfect_subarray.ipynb

(fin)