Very excited to share #SIGGRAPH2020 paper w/ @rohansawhney1 on "Monte Carlo Geometry Processing"

http://www.cs.cmu.edu/~kmcrane/Projects/MonteCarloGeometryProcessing/index.html

We reimagine geometric algorithms without mesh generation or linear solves. Basically "ray tracing for geometry"—and that analogy goes pretty deep (1/n)

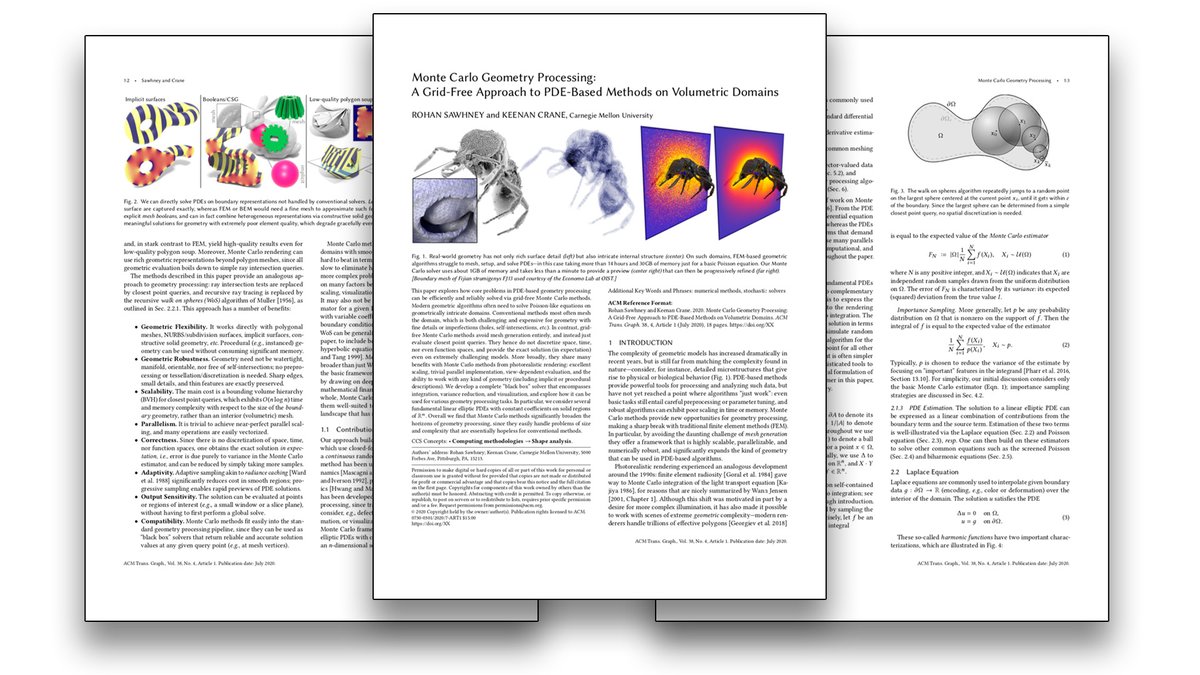
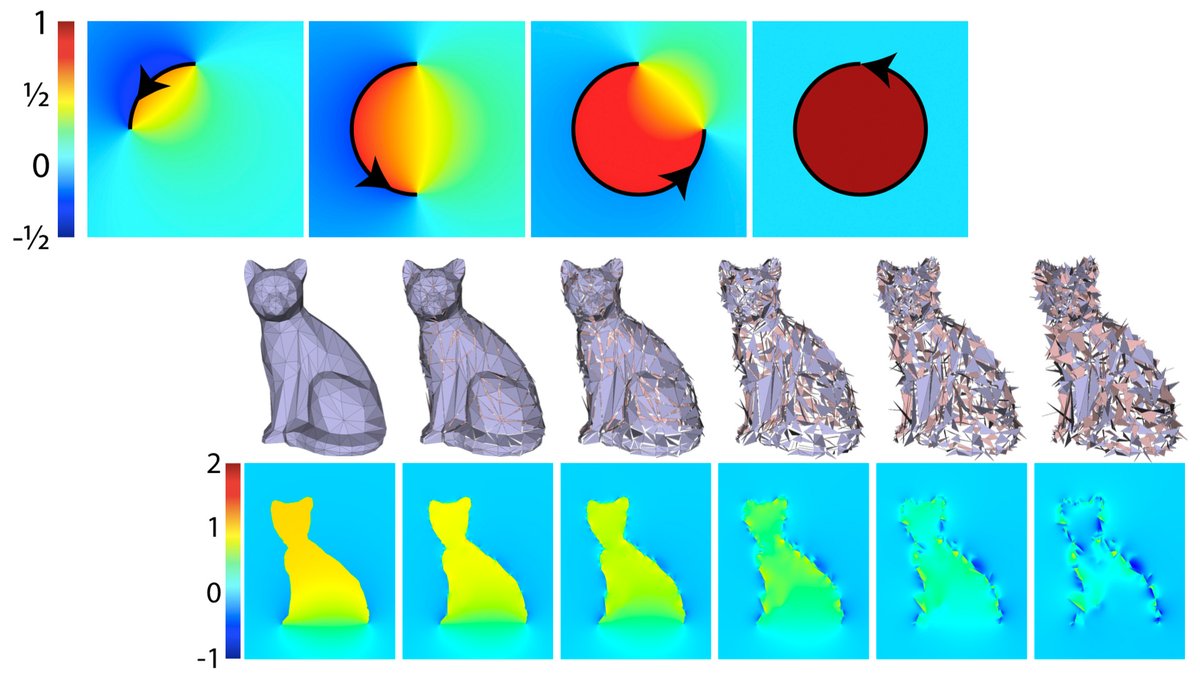
Especially for problems with super complicated geometry, not having to mesh the domain provides a massive reduction in real world end-to-end cost. For instance, this model takes 14 hours to mesh and solve w/ FEM, but less than 1 minute to preview with Monte Carlo: (2/n)

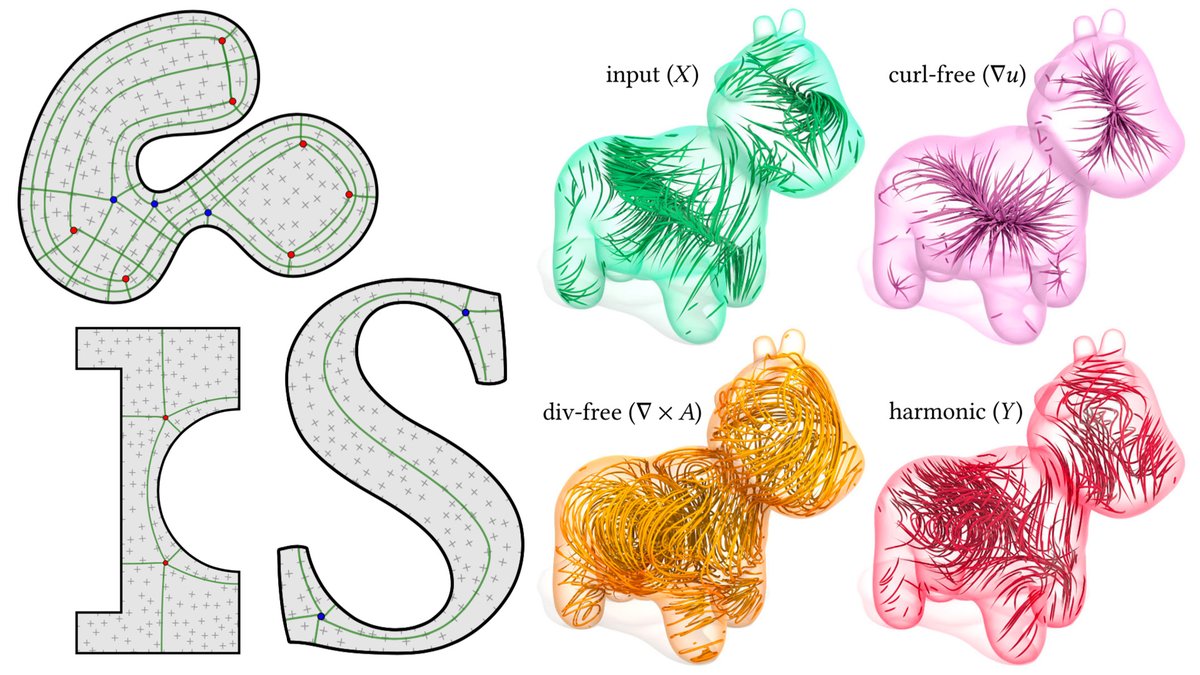
As an added bonus, we can do geometry processing directly on nonmanifold meshes, implicit surfaces, instanced geometry, CSG, Bezier curves, NURBS surfaces, etc., without doing any tessellation, sampling, mesh booleans, etc. So how does this all work? Here's the story. (3/n)

Once upon a time in rendering, finite element radiosity was the cool new thing. It let you compute some really beautiful lighting effects. But with a catch: you had to nicely mesh your domain. This was a pain, because meshing complex geometry was *hard*—and still is! (4/n)

Also, to figure out the illumination, you still had to solve a big global linear system involving every mesh node—even if you only wanted to look at a small region of the scene. (5/n)

Monte Carlo rendering takes a different approach: trace rays from the eye, and let them bounce around until they hit a light. Now, instead of meshing, the only geometric query you need is a ray-scene intersection. And you only have to compute the solution where you need it. (6/n)

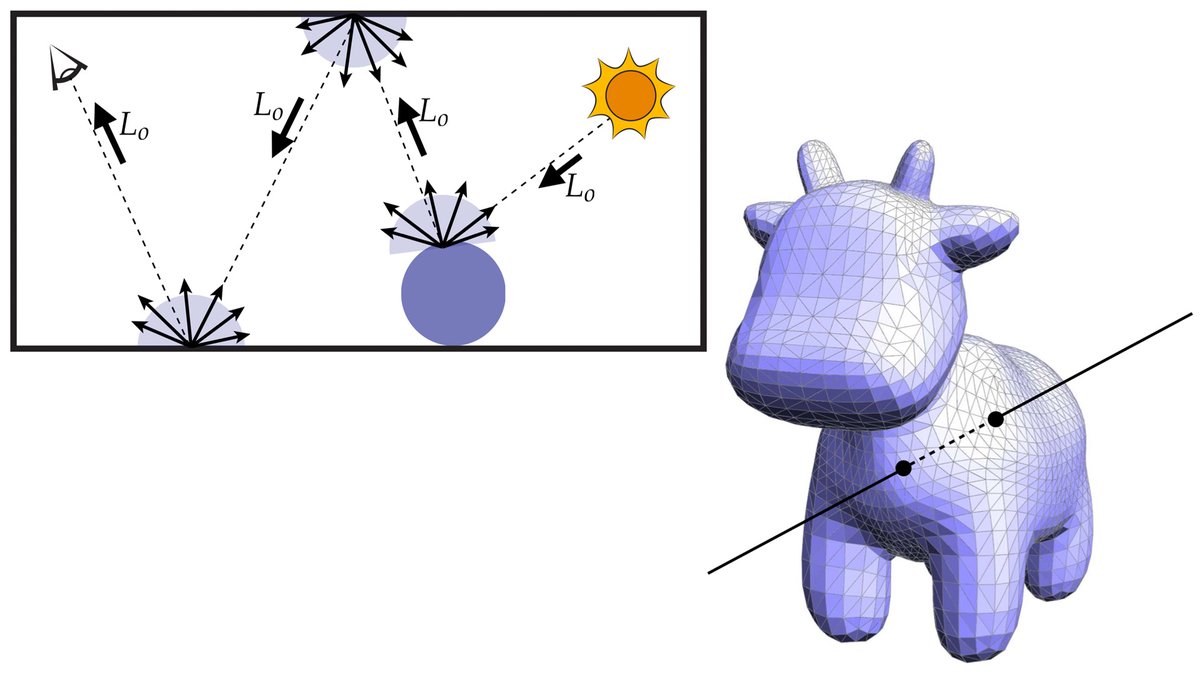
Though a big impetus for Monte Carlo rendering was more sophisticated illumination, it also enabled extremely challenging *geometry*. Even horrible meshes (from an FEM perspective) still produce gorgeous renderings. As a geometry person, this has always made me jealous! (7/n)

Our paper builds on some terrific but little-used work on stochastic PDE solvers to provide the same capabilities for geometry processing. In short: we replace Kajiya's recursive rendering equation with recursive integral equations for common PDEs (Laplace, Poisson, etc.) (8/n)

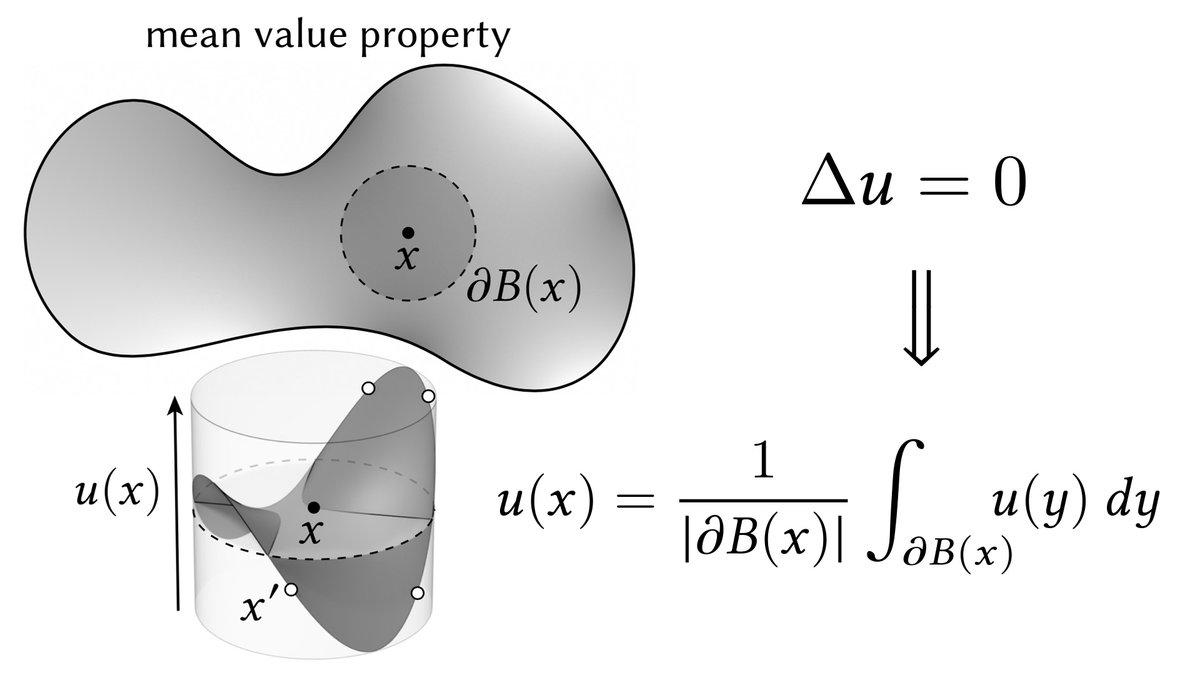
The starting point is Muller's 1956 awesome "Walk on Spheres" algorithm. Say you want to solve a Laplace equation Δu = 0 with fixed (Dirichlet) boundary values g. The mean value property says that u(x₀) equals the average of u over any sphere around x₀. (9/n)

To estimate the average, you can sample a random point x₁ on the biggest sphere around x₀ and evaluate u(x₁). In expectation, this gives *exactly* the right value. Of course, you don't know u at x₁. So, recurse. Eventually you can just grab the boundary value g(xₙ). (10/n)

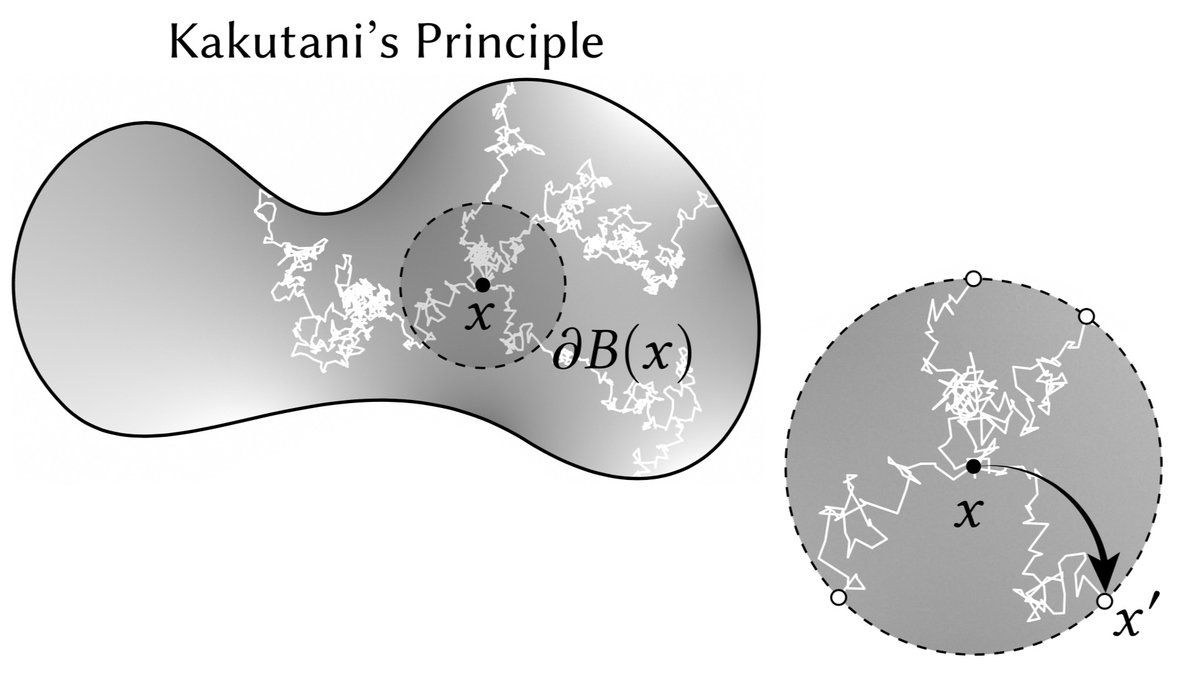
The solution to Δu = 0 is also the expected value where a random walk first hits the boundary (Kakutani's principle). How do you simulate random walks? You could take random steps on a mesh, but then you'd need a mesh! Or you could step in random directions—but how far? (11/n)

But wait: by symmetry, a random walk starting at some point x₀ is equally likely to exit through any point on a sphere around x₀—no matter how long it takes or what it does inside the sphere. So, to perfectly simulate a continuous random walk, take a walk on spheres! (12/n)

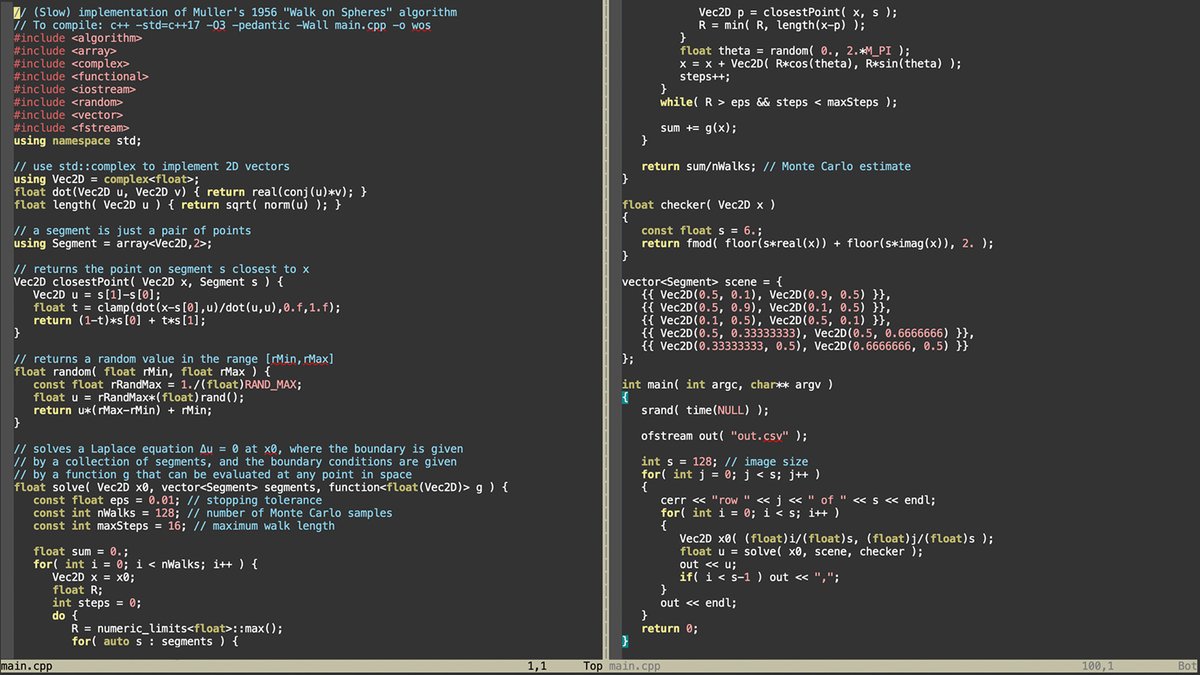
Either way, the only thing you need to know about the geometry is the size of the largest empty sphere, which you can get from a closest point query. No meshing required. Otherwise, the code can fit in a tweet—here's a full 3D Laplace solver in C++: (13/n)

float solve(Vec3D x0,vector<array<Vec3D,3>> tris,function<float(Vec3D)> g,int N){
float sum=0.f;
for(int i=0;i<N;i++){
Vec3D x=x0;
float R;
do{
R=INF;
for(auto t:tris) R=min(R,dist(x,t));
x=x+R*randSphere();
}while(R>1e-3);
sum+=g(x);
}
return sum/nWalks;
}

The only things missing are (i) how to uniformly sample the sphere and (ii) how to compute point-triangle distance. But even real code is short—here's a 2D Laplace solver (that compiles!) in 100 lines of C++: http://www.cs.cmu.edu/~kmcrane/Projects/MonteCarloGeometryProcessing/WoSLaplace2D.cpp.html (15/n)

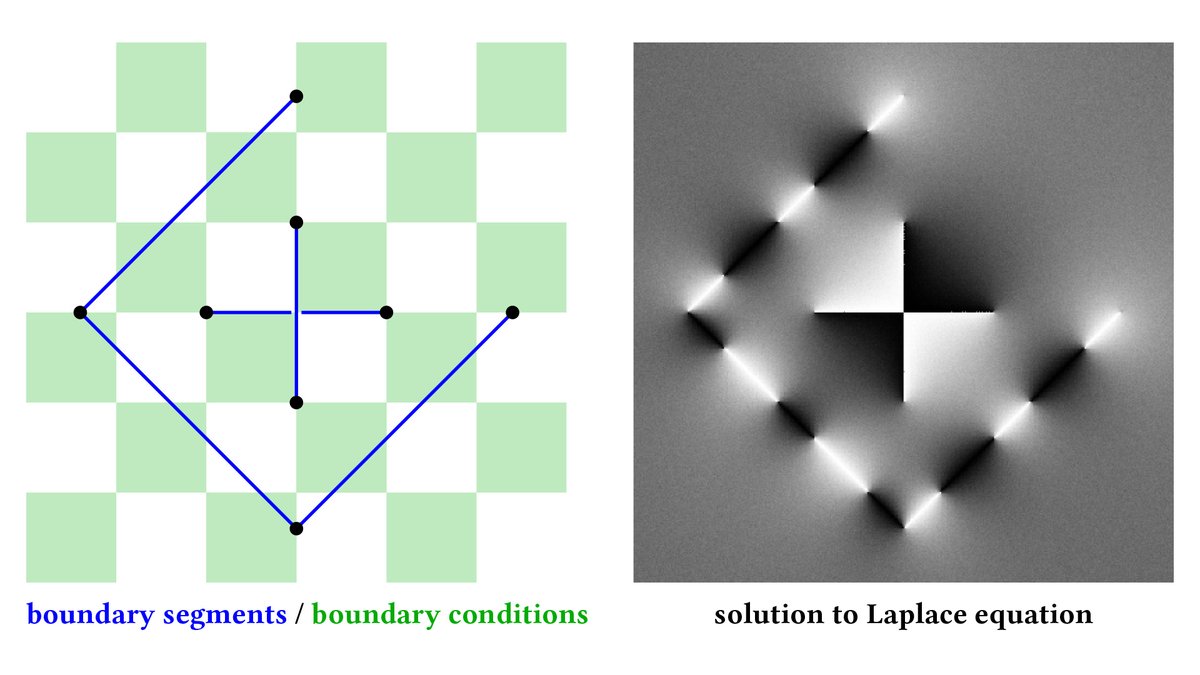
In the 2D code, you can toss in any collection of line segments (which can have intersections, holes, etc.) and a function that gives the boundary values—here, a checkerboard (in homage to rendering). It computes solution values at arbitrary points—here, a pixel grid. (16/n)

There's a nice connection here to @_AlecJacobson's generalized winding numbers https://igl.ethz.ch/projects/winding-number/ which is in essence a grid-free method for a very special PDE—and has enabled super robust mesh booleans, tet meshing, etc. But now we can solve *lots* of PDEs this way! (17/n)

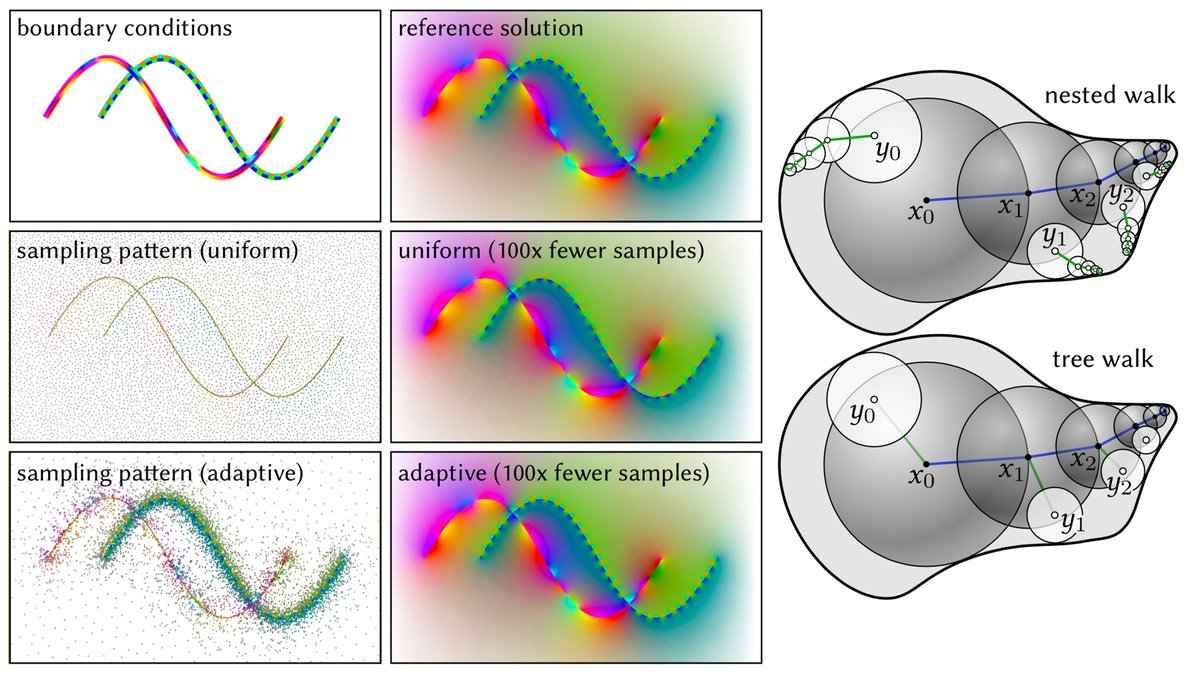
From here you can go crazy, which is what we do in the paper. You can design estimators for other PDEs, do variance reduction, adaptive sampling, etc. And the great thing is that we already have deep knowledge from the rendering community that can turbo-charge this effort. (18/n)

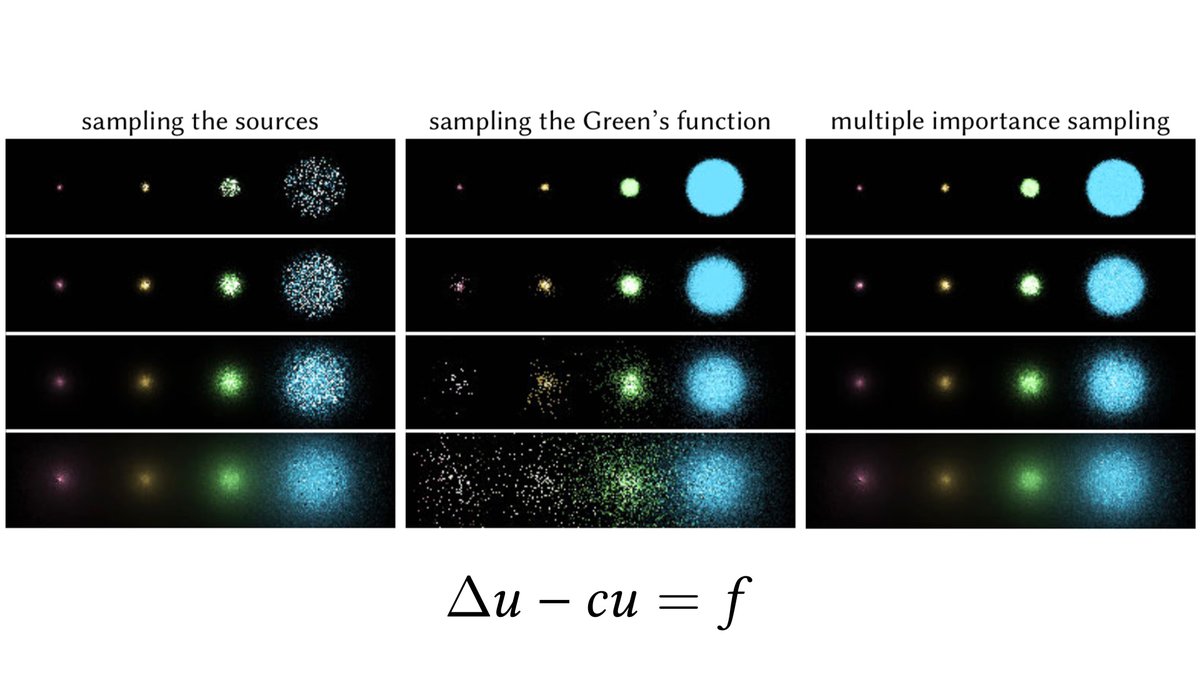
A super cool example, for instance, is that material & light importance sampling strategies from rendering have a direct analogue as Green's function & source term sampling in PDEs. So, we can use multiple importance sampling to reimagine this classic Veach demonstration: (19/n)

Of course, the whole point is to have fun with geometry. E.g., rather than hard booleans, you can blend geometry together a la @iquilezles. E.g., rather than solve PDEs on a mesh then trace streamlines, we can lazily evaluate points needed for an ODE integrator. And so on. (20/n)

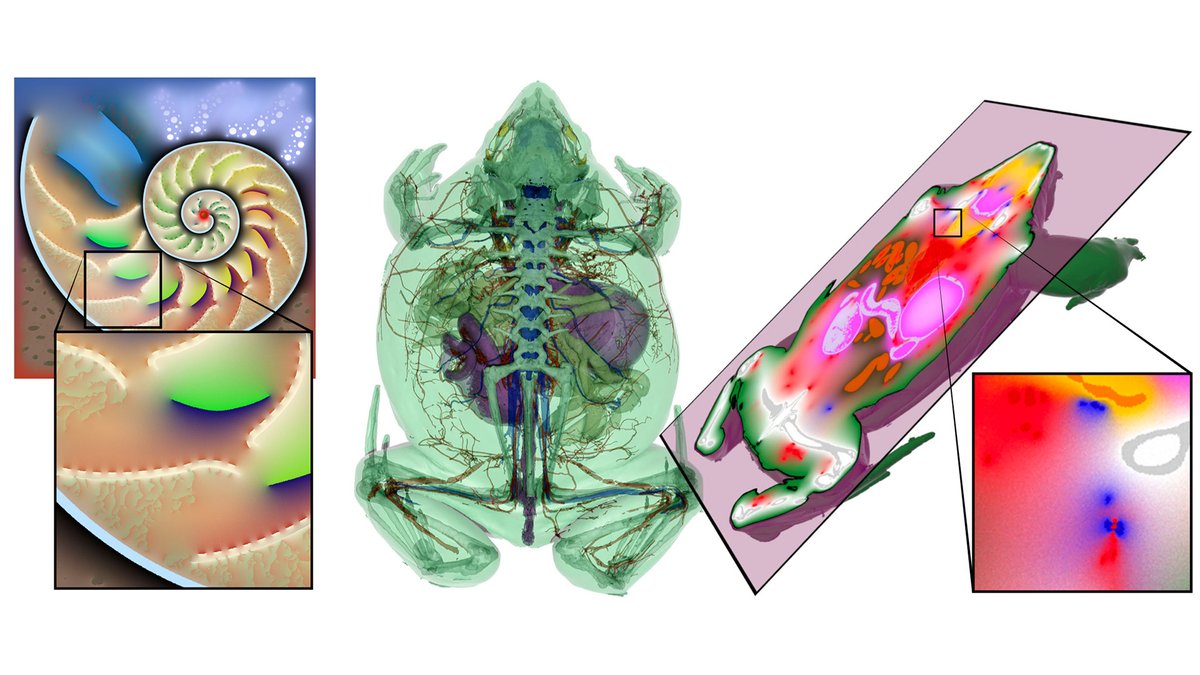
Geometric algorithms built on top of this framework share common benefits: parallel implementation is trivial; the main cost (as in ray tracing) is just doing BVH queries. Like ray tracing, we can also focus computational effort on just a region or slice plane of interest: (21/n)

Finally, this all fits into existing geometry processing pipelines. Need a solution value at a vertex? Run our black-box solver. …Ok, if I say more I'll probably just rewrite the paper here on Twitter! As you can tell, we're really excited about the possibilities. :-) (n/n)