* Disease prevalence = 1/1000
* Test false positive rate of 5%
Q: What is the chance that a random person with a positive test actually has the disease?
A question maybe even more important now 40 years after Harvard Med School docs & students were first asked.
(small thread)
* Test false positive rate of 5%
Q: What is the chance that a random person with a positive test actually has the disease?
A question maybe even more important now 40 years after Harvard Med School docs & students were first asked.
(small thread)
20 house officers, 20 attendings, and 20 4th year students.
Their answers made it in NEJM.
Probably because only 11/60 gave the correct answer.
But that was 1978, surely today medical education is much better?
Their answers made it in NEJM.
Probably because only 11/60 gave the correct answer.
But that was 1978, surely today medical education is much better?
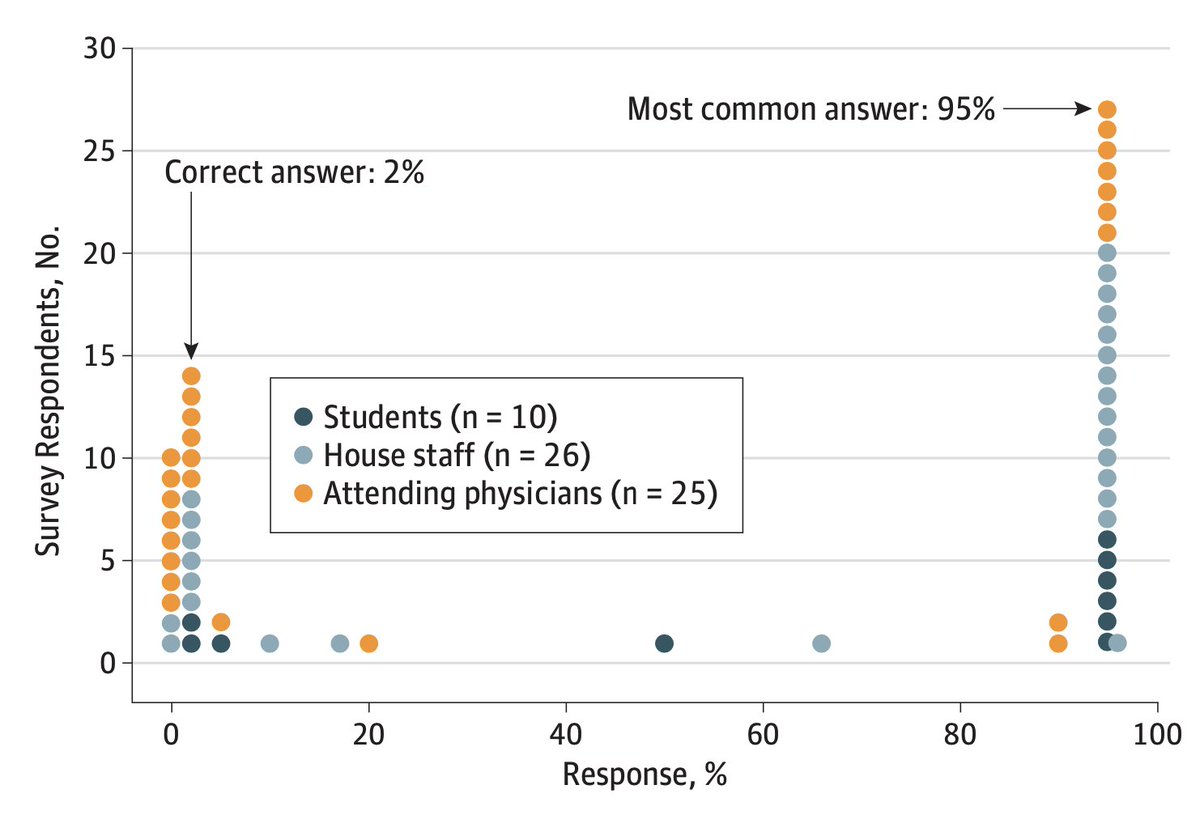
Someone thought of redoing the study in 2014. Harvard + Boston University Med Schools.
14/61 respondents answered correctly.
https://jamanetwork.com/journals/jamainternalmedicine/fullarticle/1861033">https://jamanetwork.com/journals/...
14/61 respondents answered correctly.
https://jamanetwork.com/journals/jamainternalmedicine/fullarticle/1861033">https://jamanetwork.com/journals/...
Q can be answered with epi formulas, and someone will probably objects to something in the next tweet, but a quick intuitive way of approaching it is:
- false positive rate of 5% means we have 50 false positives per 1000
- prevalence 1:1000 = in other words only 1 person in 1000 has a truly positive test
In total we have 51 positive test and only 1 true.
1:51 = 2:102 -> roughly 2%
- prevalence 1:1000 = in other words only 1 person in 1000 has a truly positive test
In total we have 51 positive test and only 1 true.
1:51 = 2:102 -> roughly 2%
Link to original NEJM piece: https://www.nejm.org/doi/full/10.1056/NEJM197811022991808">https://www.nejm.org/doi/full/...

 Read on Twitter
Read on Twitter