Read on Twitter
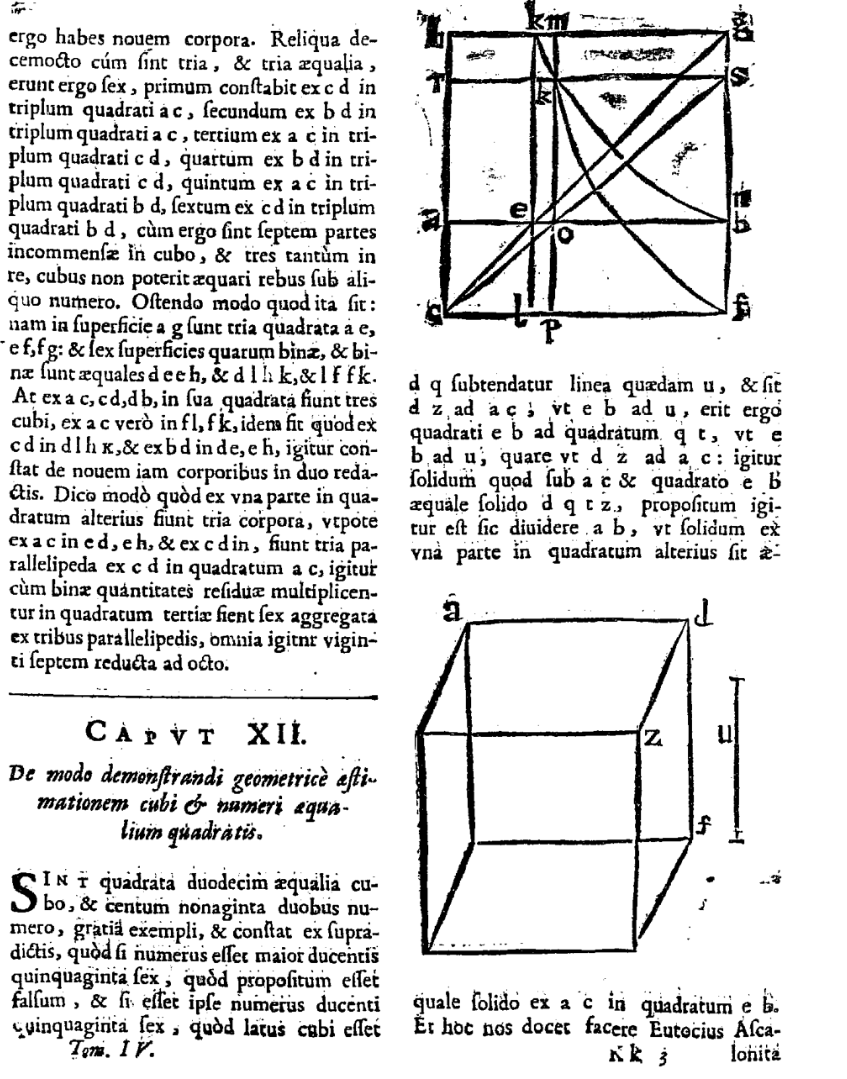
Yeah, this is one of the craziest stories in the history of math, and deserves to be better known!
In the mid-1500s, Cardano (building on del Ferro and Tartaglia, not entirely amicably...) solved the cubic equation. The solution goes something like this. https://twitter.com/3blue1brown/status/1253747012245221376">https://twitter.com/3blue1bro...
In the mid-1500s, Cardano (building on del Ferro and Tartaglia, not entirely amicably...) solved the cubic equation. The solution goes something like this. https://twitter.com/3blue1brown/status/1253747012245221376">https://twitter.com/3blue1bro...
2/ You want to solve ax^3+bx^2+cx+d=0. First make it "monic" (leading coefficient 1) by dividing by "a". Renaming coefficients, we have:
x^3+Bx^2+Cx+D=0.
Now "depress" it (kill off x^2 term) by replacing x=y-B/3. After some algebra, we have:
y^3+my+n=0.
[Aside: when you do...
x^3+Bx^2+Cx+D=0.
Now "depress" it (kill off x^2 term) by replacing x=y-B/3. After some algebra, we have:
y^3+my+n=0.
[Aside: when you do...
3/ the same with a quadratic, ax^2+bx+c=0, divide by "a", and set y=x-B/2, you get y^2+n=0. This recently "rediscovered" method of solving quadratics is what @3blue1brown explained in his last live session. Shows how poorly we teach quad equations that NYT thinks it& #39;s new...]
4/ Back to y^3+my+n=0. By a beautiful method (which I can explain elsewhere), Cardano derives the formula:
y=u-v,
where (crt=cube root)
u=crt[-n/2+sqrt R],
v=crt[n/2+sqrt R],
and
R=n^2/4+m^3/27.
Now, I made two claims in my message to Grant:
y=u-v,
where (crt=cube root)
u=crt[-n/2+sqrt R],
v=crt[n/2+sqrt R],
and
R=n^2/4+m^3/27.
Now, I made two claims in my message to Grant:
5/
(1) That negative numbers did *not* exist at this time,
but shockingly that
(2) Complex numbers were needed as an "abstract tool" to solve "real" problems!
Let me first argue (1). Cardano first solves y^3+my=n, then y^3=my+n, then y^3+n=my, etc. Aren& #39;t these all the same??
(1) That negative numbers did *not* exist at this time,
but shockingly that
(2) Complex numbers were needed as an "abstract tool" to solve "real" problems!
Let me first argue (1). Cardano first solves y^3+my=n, then y^3=my+n, then y^3+n=my, etc. Aren& #39;t these all the same??
6/ No! Because to Cardano (like Euclid!), y^3 literally means a y×y×y cube!
That is, they are not overloading the "-" symbol (as we do today, and confuse poor pre-algebra students!) to mean both subtraction and negation. Negative numbers don& #39;t exist!
So how could complexes???
That is, they are not overloading the "-" symbol (as we do today, and confuse poor pre-algebra students!) to mean both subtraction and negation. Negative numbers don& #39;t exist!
So how could complexes???
7/ Look back at Cardano& #39;s formula. Let& #39;s solve, e.g.,
y^3-15y-4=0.
One can easily stumble on to y=4 as a solution. But what does Cardano& #39;s formula give? y=u-v where:
R=n^2/4+m^3/27 = -121
and
u=crt[-n/2+sqrt R]=crt[2+sqrt(-121)],
v=crt[-2+sqrt(-121)].
Huh? Here& #39;s Bombelli& #39;s
![7/ Look back at Cardano& #39;s formula. Let& #39;s solve, e.g.,y^3-15y-4=0.One can easily stumble on to y=4 as a solution. But what does Cardano& #39;s formula give? y=u-v where:R=n^2/4+m^3/27 = -121andu=crt[-n/2+sqrt R]=crt[2+sqrt(-121)],v=crt[-2+sqrt(-121)].Huh? Here& #39;s Bombelli& #39;s](https://pbs.twimg.com/media/EWZkBV3XQAEC7GB.jpg "7/ Look back at Cardano& #39;s formula. Let& #39;s solve, e.g.,y^3-15y-4=0.One can easily stumble on to y=4 as a solution. But what does Cardano& #39;s formula give? y=u-v where:R=n^2/4+m^3/27 = -121andu=crt[-n/2+sqrt R]=crt[2+sqrt(-121)],v=crt[-2+sqrt(-121)].Huh? Here& #39;s Bombelli& #39;s")
y^3-15y-4=0.
One can easily stumble on to y=4 as a solution. But what does Cardano& #39;s formula give? y=u-v where:
R=n^2/4+m^3/27 = -121
and
u=crt[-n/2+sqrt R]=crt[2+sqrt(-121)],
v=crt[-2+sqrt(-121)].
Huh? Here& #39;s Bombelli& #39;s
8/ workaround: Ok, "imagine" that all of this makes sense, which it doesn& #39;t, and notice (writing i=sqrt(-1)) that:
(2+i)^3=2^3+3*2^2*i+3*2*i^2+i^3=2+sqrt(-121).
So we must have that
u=crt[2+sqrt(-121)]=2+i.
And similarly, v=-2+i. So:
y=u-v=(2+i)-(-2+i) = 4!!!
This nonsense
(2+i)^3=2^3+3*2^2*i+3*2*i^2+i^3=2+sqrt(-121).
So we must have that
u=crt[2+sqrt(-121)]=2+i.
And similarly, v=-2+i. So:
y=u-v=(2+i)-(-2+i) = 4!!!
This nonsense
9/ isn& #39;t "real", but it& #39;s a *useful tool* to get at the real answer. Complex numbers existed in this limbo long before they became "the complex plane" in work of Euler/Argand/Wessel. But there you have it, complex numbers were needed well before negatives!
#mbtos #iteachmath
#mbtos #iteachmath
PS A great exposition of this story, as well as the Cardano/Tartaglia feud, is in Dunham& #39;s fantastic book, "A Journey Through Genius" (which is where I first read about it).
