Tectonic issues raised by the movie “Piranha 3-D” (A. Aja, 2010, Dimension Films): The lockdown-induced geology thread absolutely no one asked for. (1/n)
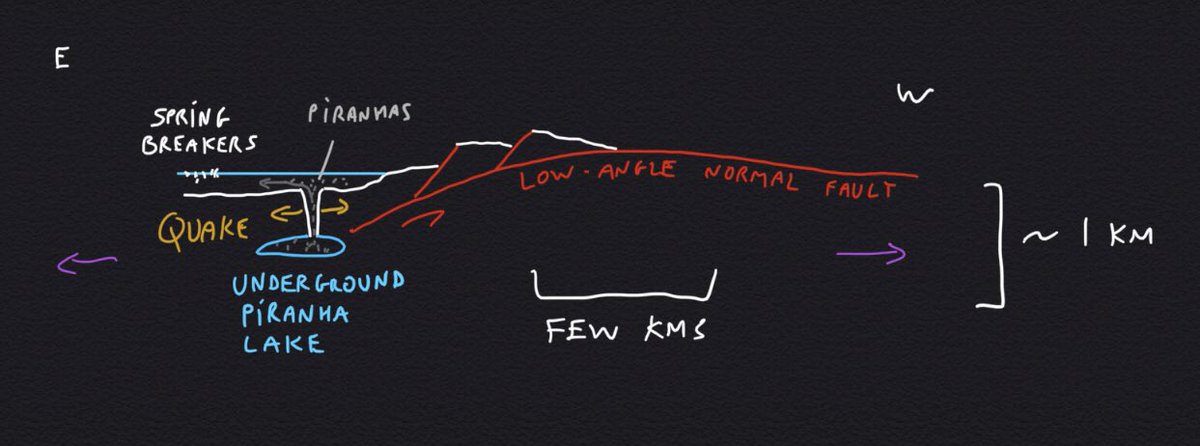
The premise of this cinematic masterpiece is that an earthquake opens a pathway between a subterranean lake full of hungry prehistoric piranhas and Lake Havasu (renamed Lake Victoria). Also, it’s Spring Break. (2/n) https://youtu.be/NdMO51GaTMs ">https://youtu.be/NdMO51GaT...
The earthquake is pictured as a mode-I (tension) crack straight up opening at the bottom of the lake. (3/n)
That’s a staple of bad geology movies (e.g., San Andreas, The Rock et al., 2015): real quakes are dominated by motion parallel, not perpendicular to the fault, because the weight of rocks makes it difficult to open cracks at depth in the crust (we’ll get back to that). (4/n)
But what if in this specific case a tensional earthquake made sense? Hear me out. (5/n)
Lake Havasu (AZ/CA, USA) is located in an area of crustal stretching, right by the Whipple Mountains, a metamorphic core complex formed by slip on a low-angle (<<15 degrees), very-large offset, east-dipping detachment (normal) fault. (6/n)
This is relevant for the tensile-quake-releasing-piranhas story because low-angle normal faulting may indicate a somewhat unusual state of stress in the brittle upper crust. (7/n)
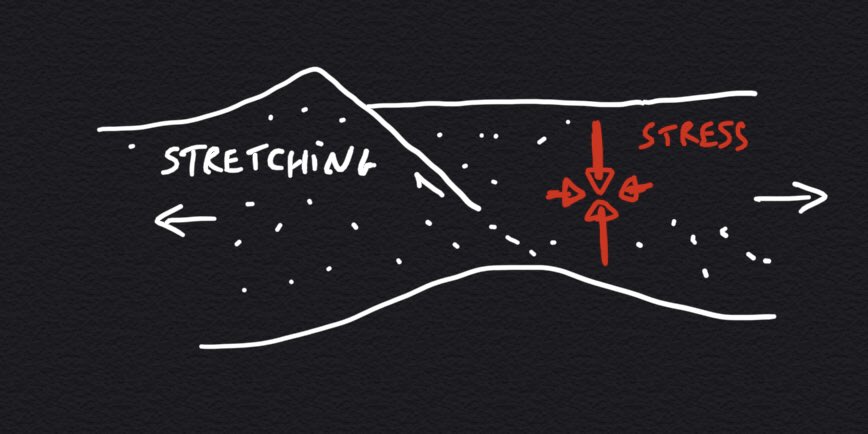
We usually think of stresses in extending crust as the sum of: (1) pressure due to the weight of the rocks above you, (2) perhaps some pressurized fluids in the pores of rocks “pushing outward”, and (3) a horizontal *deviatoric* stress, which drives the stretching. (8/n)
Note that, in the above configuration, the total horizontal stress usually remains compressional, meaning that summing the white, blue and purple horizontal arrows results in arrows that point inward. (9/n)
That’s right: even in regions of crustal stretching stresses are overall compressional, they’re just a bit less compressional along the horizontal than along the vertical direction. (10/n)
There is still a possibility, however, for the total horizontal stress to become tensile, either because fluid pressure is very high, or because the deviatoric stress is large (or both)… allowing vertical hydrofracture, i.e. tensile piranhaquake. (11/n)
So–– is this a plausible situation at Lake Havasu, near the Whipple detachment fault? (12/n)
Slip on a fault requires a shear stress proportional to the normal stress. It’s like putting your hand flat on a table, applying pressure, and trying to slide it sideways. The harder you push (greater normal stress), the harder it is to slide (needs greater shear stress). (13/n)
A quasi-horizontal normal fault like the Whipple detachment feels a LOT of vertical compression, and thus needs a large shear stress to move.
(14/n)
(14/n)
This large shear stress is directly related to the deviatoric tensional stress (purple arrows): if it went away, there would be no shear on the fault, just uniform squeezing. The point is: slip on a low-angle normal fault requires a large deviatoric stress. (15/n)
This last point is why low-angle normal faults are often regarded as a mechanical paradox. Breaking a steep (60º) normal fault requires a much lower deviatoric stress than slipping on a low-angle fault. (16/n)
So why would our lazy Earth (shout out to @geomechCooke) bother to spend all that energy slipping on shallow-dipping faults when it could just break steep new ones? A great question for another thread, we’re supposed to be talking about prehistoric piranhas here. (17/n)
A possible solution to the “paradox” could be that fluids in the pores of the crust (and in the subterranean piranha lake) are pressurized. This happens when pores are not well connected and water is having a hard time moving through them. (18/n)
Fluid pressure can alleviate a large portion of the rock pressure squeezing the fault, in which case the fault no longer needs a large deviatoric stress to move. (19/n)
But it also means that even a small deviatoric stress can push you over the edge and drive net horizontal tension, opening vertical, fish-filled cracks. (20/n)
Many authors have noted, however, that as soon as hydrofracture occurs fluid pressure should drop. This is because fluids and fishes can now move freely through the new cracks. (21/n)
But if cracks end up healing, fluids can become trapped again and build up pressure until the next hydrofracture event. (22/n)
So there you have it. A region of deviatoric horizontal tension coupled with high fluid pressure could enable low-angle normal faulting AND the occasional hydrofracture event, i.e., the timely release of prehistoric piranhas during Spring break. Except… (23/n)
Except the Whipple detachment has not slipped much in the last 10+ million years… and even when it did, it is not clear that the fault surfaces we now see exposed at low angles actually slipped at low angles below ground. (24/n)
In fact, recent work by Gans & Gentry suggests that the Whipple detachment fault actually slipped at steeper angles but experienced rotation as it accumulated offset ( https://agupubs.onlinelibrary.wiley.com/doi/full/10.1002/2016TC004215).">https://agupubs.onlinelibrary.wiley.com/doi/full/... So there may be no need to invoke high fluid pressures in the region. (25/n)
That’s not to say that slip on low-angle normal faults is not a thing ( @GeoNickHayman !). Classic thermochronology studies even suggest that the Chemehuevi detachment just 10 km N of Lake Havasu did slip at 15–30º, ~20 Myrs ago (John & Foster, 1993). (26/n)
But it leads us to conclude that while a tensional piranhaquake seems unlikely today at the AZ/CA border, it plausibly occurred during the early Miocene, while tiny mammals were on Spring Break.
A closer look at the fossil record is thus warranted. (27/27)
A closer look at the fossil record is thus warranted. (27/27)

 Read on Twitter
Read on Twitter