Ever wonder what the heck an Echo State Network (ESN) is, or what the fuss is all about and how it relates to recurrent neural networks (RNNs) more generally? Follow along in this tweet storm. https://abs.twimg.com/emoji/v2/... draggable="false" alt="🐦" title="Bird" aria-label="Emoji: Bird">https://abs.twimg.com/emoji/v2/... draggable="false" alt="⚡️" title="High voltage sign" aria-label="Emoji: High voltage sign">

aka day 93 in quarantine = tweeting about random stuff
Preliminaries - An ESN is an RNN with fixed, random weights in the recurrent and input matrices but the readout matrix is trained. The output weights are trained via linear regression to make the outputs look like desired targets.
In contrast, an RNN used in deep learning applications is trained with back-propagation through time (BPTT), training all the parameters. BPTT allows an error at time t to be combine with activity at a time earlier than t to modify the weights.
The neuroscience community has been interested in ESNs for well over a decade because you can train reasonably complicated input/output relationships without BPTT. Remember that the norm-core consensus opinion is that BPTT is likely not implemented in the brain.
Also, a small community of optics researchers have been using the ESN model to train computers made of light, for similar reasons (they cannot backprop through the optics components).
Another related model is the Liquid State Machine (by Maass and colleagues). This is very similar to ESN except it uses spiking neural networks. I won’t be discussing LSMs any further but it’s good to know this acronym because it comes up (just think spiking ESN).
Here is the equation for the ESN, it’s very similar to a “Vanilla RNN” with a linear readout. r is the hidden state, u the input, and z is the readout (1-D readout for simplicity).
ESNs come in two flavors, those with feedback of the output into the hidden state, and those that do not feed back the output. Adding feedback just augments the original equation. This difference is absolutely critical.
If an ESN does not have output feedback, then it is truly a random “reservoir”, simply nonlinearly filtering the inputs. Study this triangle wave input (red) driving the reservoir. The reservoir creates both phase shifts and nonlinear harmonics of the triangle wave (blue).
If the input stops, then the hidden unit dynamics will go back to doing whatever they were doing before the input came on, for example with spontaneous activity as shown here for a few hidden units (blue).
However, if the ESN has output fed back to the reservoir, then the reservoir is not random. In fact, what you are doing is training a rank-1 (for a 1-d output) outer-product perturbation to J (namely training J+uw& #39;):
Remember that modifying either u or w is sufficient to change every single eigenvalue of (J + uw^T), though not the eigenvectors! Thus, one can change the dynamics (shrinking, stretching, oscillating), but not the spatial arrangement of those dynamics in state-space.
When one trains an ESN, one defines a target function, f(t), and an *instantaneous error*, e(t) = z(t) - f(t). You use linear regression to train w, and voila, you very easily have a system that performs your task. There is no BPTT.
In practice, folks use FORCE learning (my PhD thesis! https://abs.twimg.com/emoji/v2/... draggable="false" alt="😊" title="Smiling face with smiling eyes" aria-label="Emoji: Smiling face with smiling eyes">), a recursive least squares technique, because it stabilizes the network, but that is outside the scope of this tweet storm.
Thus after training, an ESN with feedback can sustain the dynamics it was trained to generate. In this case, now the triangle wave is the output, and the network is able to sustain it indefinitely.
It is often stated that ESNs cannot perform as well as RNNs with BPTT in hard tasks. I suspect this is true, but there is room for caution. First, both ESNs and RNNs are universal approximators.
Second, I haven’t ever seen a head-to-head comparison that is done on a per-parameter basis. Keep in mind that the ESN has only O(ZN) trainable params for an N-dim network with Z-dim output, whereas a Vanilla RNN has O(N^2 + ZN). Doing this correctly is tricky.
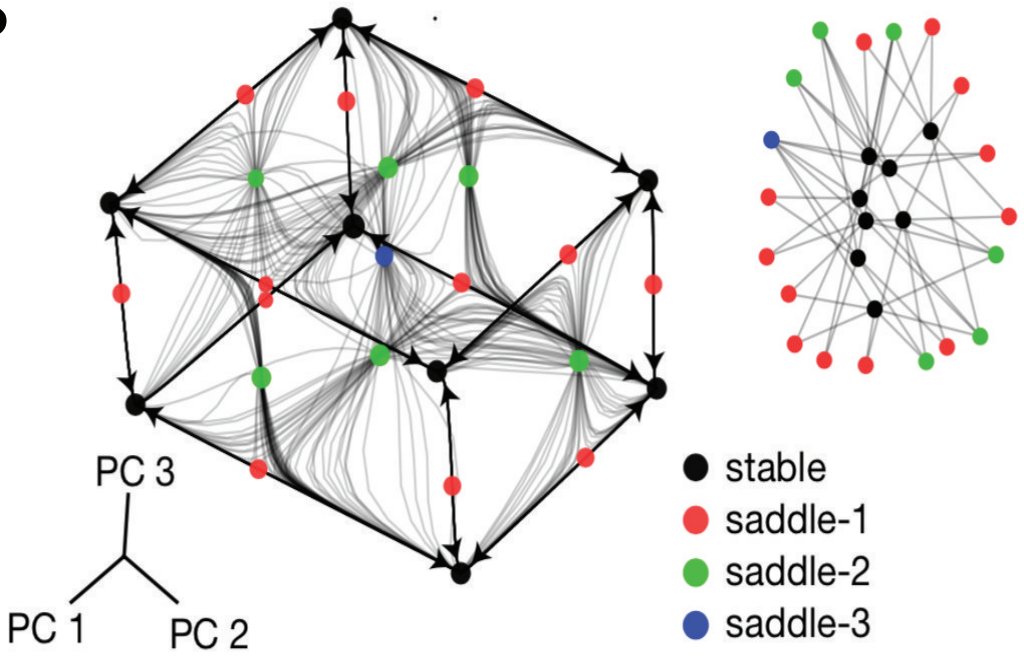
Finally, I want to highlight that ESNs with feedback learn non-random representations! Take the toy 3-bit memory task: there are 3 inputs and 3 outputs. Output a should remember the sign of the last input deflection on input a, and so on for input/output pairs a, b, c.
Here is a PCA plot of the state-space representation for the trained ESN, including what I call the “dynamical skeleton”, which are the fixed points, saddle points and heteroclinic orbits that mediae the nonlinear dynamics. That is representation in RNN land.
Here is a similar PCA plot (different paper but same idea) for an RNN with all parameters trained fully with BPTT. (GRU, LSTM, VRNN all look identical, btw). It looks awfully similar to the ESN whose output weights were trained and fed back.
That’s it! Thanks for reading!
https://abs.twimg.com/emoji/v2/... draggable="false" alt="🤘" title="Sign of the horns" aria-label="Emoji: Sign of the horns">https://abs.twimg.com/emoji/v2/... draggable="false" alt="🤓" title="Nerd face" aria-label="Emoji: Nerd face">https://abs.twimg.com/emoji/v2/... draggable="false" alt="🤘" title="Sign of the horns" aria-label="Emoji: Sign of the horns">
Here are the refs I used:
(Jaeger, Haas 2004) https://pdfs.semanticscholar.org/8922/17bb82c11e6e2263178ed20ac23db6279c7a.pdf

(Sussillo,">https://pdfs.semanticscholar.org/8922/17bb... Abbott 2009) https://www.sciencedirect.com/science/article/pii/S0896627309005479

(Sussillo,">https://www.sciencedirect.com/science/a... Barak 2013) https://www.mitpressjournals.org/doi/full/10.1162/NECO_a_00409

(Maheswaranathan">https://www.mitpressjournals.org/doi/full/... et al, 2019) https://papers.nips.cc/paper/9694-universality-and-individuality-in-neural-dynamics-across-large-populations-of-recurrent-networks.pdf

(Maass">https://papers.nips.cc/paper/969... et al. 2002) https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.183.2874&rep=rep1&type=pdf">https://citeseerx.ist.psu.edu/viewdoc/d...
Opening the Black Box: Low-Dimensional Dynamics in High-Dimensional Recurrent Neural Networks

Opening the Black Box: Low-Dimensional Dynamics in High-Dimensional Recurrent Neural Networks

https://pdfs.semanticscholar.org/8922/17bb82c11e6e2263178ed20ac23db6279c7a.pdf
You can follow @SussilloDavid.
Tip: mention @twtextapp on a Twitter thread with the keyword “unroll” to get a link to it.

Latest Threads Unrolled:
There are a lot of misconceptions about the Turkish diaspora in Germany. Since i just finished writing an essay about this topic I thought it's time to give other people
Read more
Las mejores calculadoras online en 2020A thread http://totumat.com/2020/11/26/las-mejores-calculadoras-online-en-2020/ Cuando se estudian asignaturas que requieren de cålculos complicados, nada mejor que contar con una buena calculadora.
Read more
Mitigating #ClimateChange is as much about taking up new techs as about leaving others behindMost studies focus on #coal's global downfall but another #energy tech decline is loomingRead my new
Read more