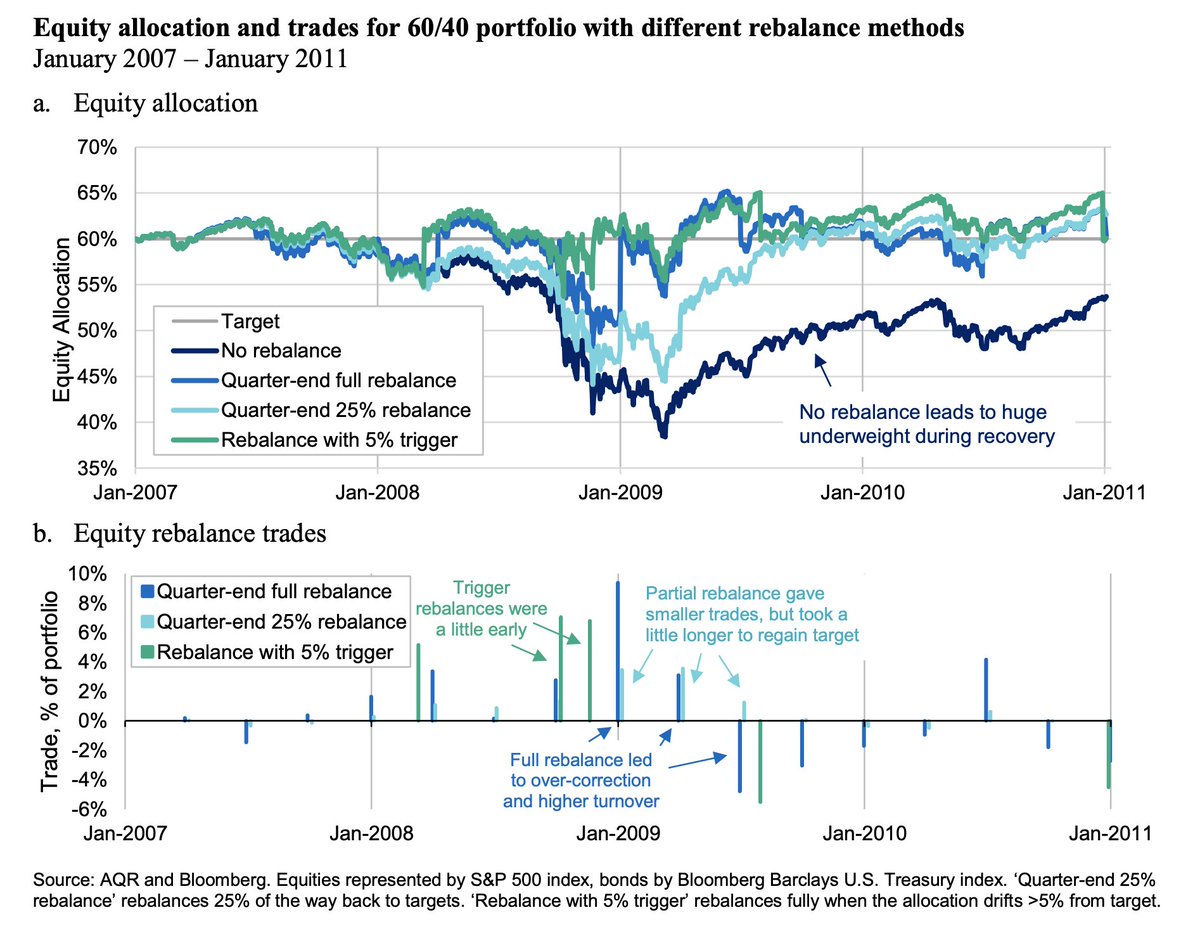
1/ New piece from AQR crossed my desk.
"When to rebalance your portfolio? Little, often, and unswayed by tactical views.”
You know this is my jam.
So a quick thought on tranched rebalancing and fighting the trend...
"When to rebalance your portfolio? Little, often, and unswayed by tactical views.”
You know this is my jam.
So a quick thought on tranched rebalancing and fighting the trend...
2/ It’s been long established that rebalancing is, inherently, a mean-reversionary strategy.
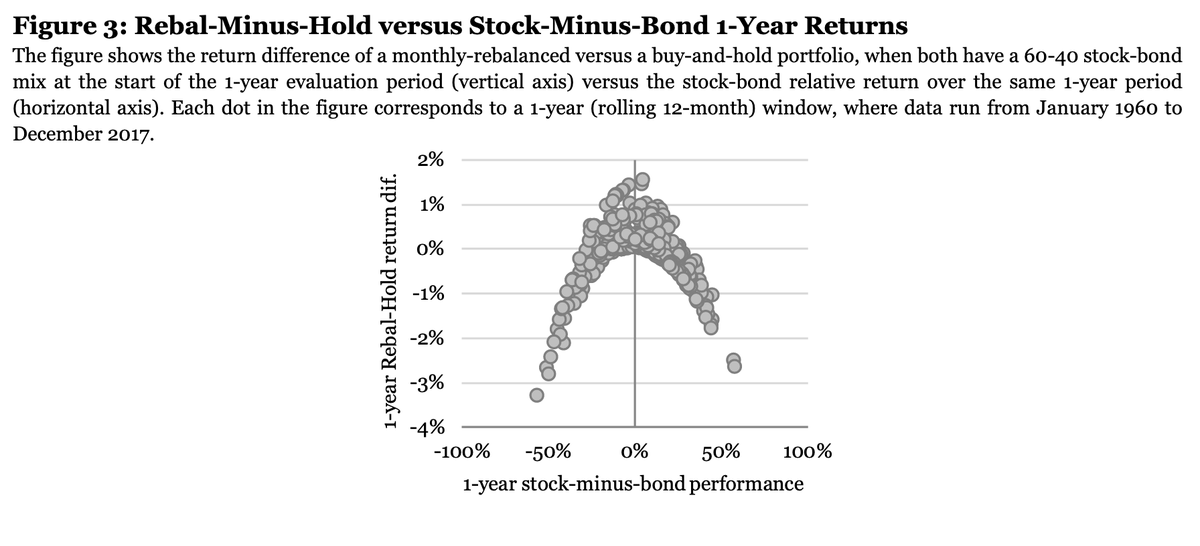
I think this is best captured – at least visually – in the paper Strategic Rebalancing ( https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3330134),">https://papers.ssrn.com/sol3/pape... which plots B&H vs monthly rebalance returns for a 60/40.
I think this is best captured – at least visually – in the paper Strategic Rebalancing ( https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3330134),">https://papers.ssrn.com/sol3/pape... which plots B&H vs monthly rebalance returns for a 60/40.
3/ We clearly see concavity.
Now, most folks I speak to don’t rebalance 100% of their portfolio every month.
What’s more likely is an annual rebalance. Which, as I’ve demonstrated many times ( https://jii.pm-research.com/content/10/1/27.abstract)">https://jii.pm-research.com/content/1... exhibits significant rebalance timing luck.
Now, most folks I speak to don’t rebalance 100% of their portfolio every month.
What’s more likely is an annual rebalance. Which, as I’ve demonstrated many times ( https://jii.pm-research.com/content/10/1/27.abstract)">https://jii.pm-research.com/content/1... exhibits significant rebalance timing luck.
4/ The answer? Tranching.
e.g. instead of an annual rebalance, you rebalance 1/12th of your portfolio every month (basically, you correct for 1/12th of the drift).
e.g. instead of an annual rebalance, you rebalance 1/12th of your portfolio every month (basically, you correct for 1/12th of the drift).
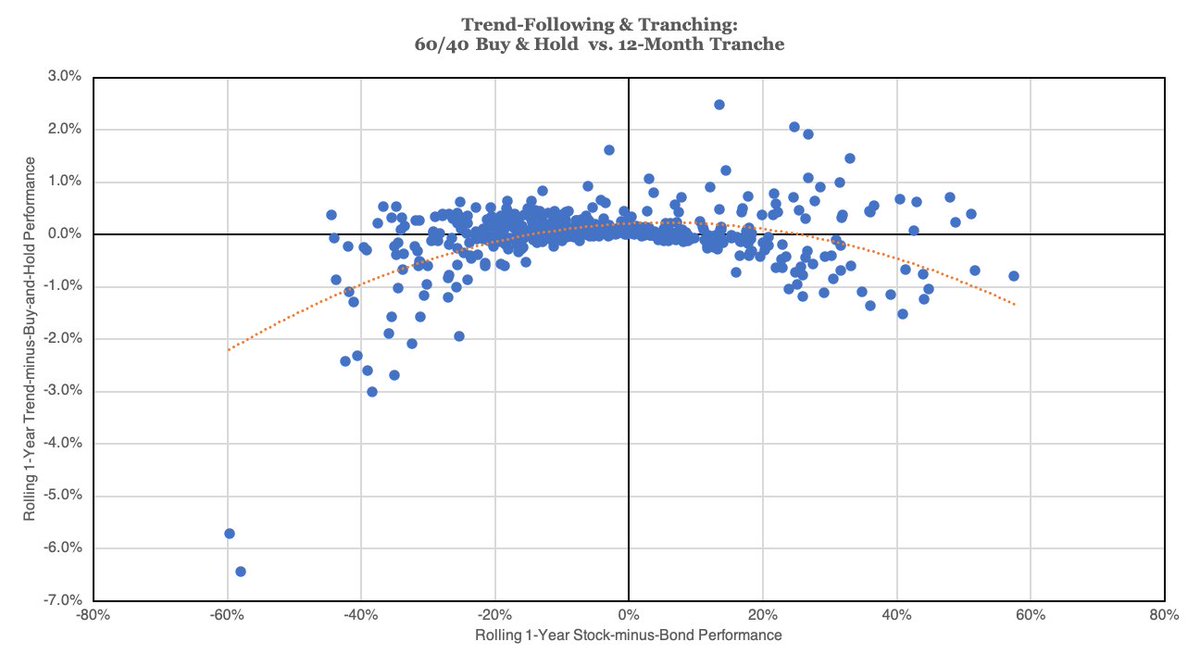
5/ But if you believe in trend (which, I do), then tranching also helps inject a little trend into your life.
Consider the left graph (the payoff profile of a full monthly rebalance) versus the right (the payoff profile of a 1/12th tranche).
Consider the left graph (the payoff profile of a full monthly rebalance) versus the right (the payoff profile of a 1/12th tranche).
6/ The payoff profile flattens because we’re combining a concave payoff (rebalancing) with a convex one (trend / autocorrelation).
This looks almost the same as the result of taking a strategic portfolio and adding a trend sleeve! https://blog.thinknewfound.com/2020/02/payoff-diversification/">https://blog.thinknewfound.com/2020/02/p...
This looks almost the same as the result of taking a strategic portfolio and adding a trend sleeve! https://blog.thinknewfound.com/2020/02/payoff-diversification/">https://blog.thinknewfound.com/2020/02/p...
7/ That’s because the tranche method basically lets each part of the portfolio “run” for the set time.
e.g. a 12-month tranche lets each 12th of the portfolio “run” for 12 months. If you believe trend is exhibited over that period, you might harvest some benefits.
e.g. a 12-month tranche lets each 12th of the portfolio “run” for 12 months. If you believe trend is exhibited over that period, you might harvest some benefits.
8/ Thanks to @millerak42 for inspiring some investigation here.

 Read on Twitter
Read on Twitter