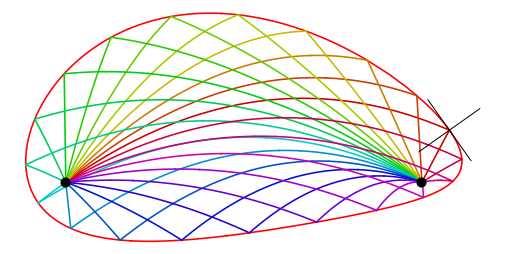
[1/2] It’s well known that an ellipse will reflect any straight line trajectory from one focus so it passes through the other focus, but what about the parabolic trajectories of an object moving under gravity?

Here the red curve will reflect any object leaving the “launch point”

[2/2] with a particular speed into a trajectory that passes through the “target point”.

[Inspired by (though different from) a basketball backboard that renders almost any shot successful. Thanks to @octonion!

https://twitter.com/octonion/status/1251337469347467264 ]

Here’s the complete curve, including upwards bounces (thanks to @TobyBailey for suggesting it).

Here’s a more symmetrical version, where the launching point and the target are at the same height.

Why is this different from the curve you get by letting an ellipse free fall, while particles are reflected between its foci, recording the position of each point on the ellipse when a particle hits it?

Because the normal to *that* curve won’t correctly reflect the trajectories.

Gravity & velocity combined give us a parameter:

β=g/v^2

The highest β allowed is when some trajectory grazes the reflector. For a symmetrical configuration, this is:

β_m = 8z/(16z^2+x^2)

where z is the height of the top of the reflector and x is the distance between foci.

Fine print: in fact, that β_m is a bit higher than the value that can actually be allowed, because it’s the β such that the top of a symmetric parabolic trajectory would touch the top of the reflector. A grazing trajectory occurs at a slightly lower value.