Read on Twitter
Suite aux nombreux graphiques que l& #39;on voit passer pour l& #39;instant, certaines personnes s& #39;interrogent sur l& #39;utilité d& #39;une échelle "pas linéaire" ou "bizarre" ou "qui donne une fausse impression"
petit #thread illustré pour expliquer l& #39;échelle logarithmique 1/7
petit #thread illustré pour expliquer l& #39;échelle logarithmique 1/7
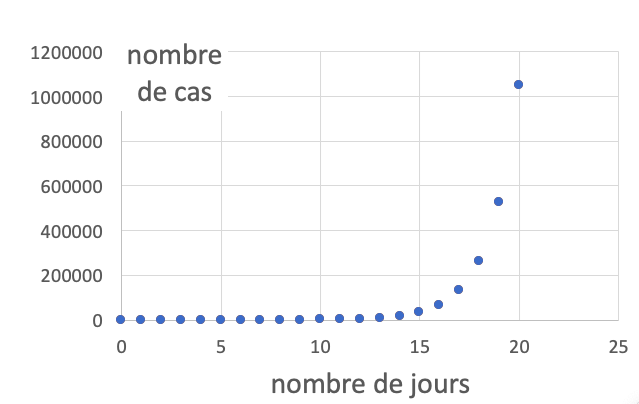
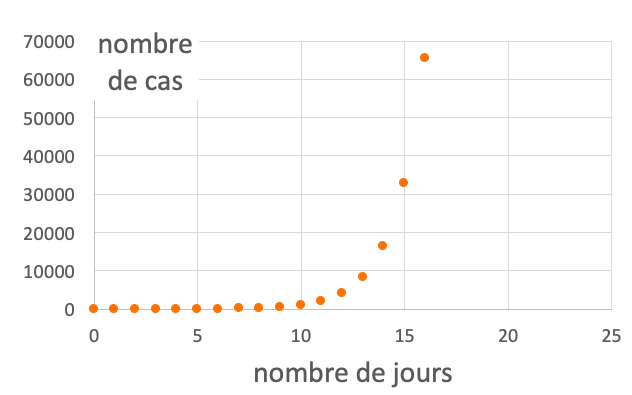
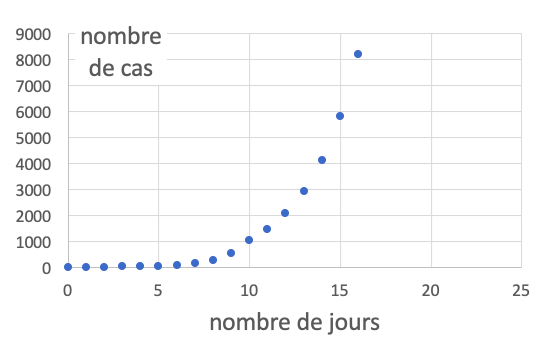
imaginons que l& #39;on cherche à étudier un phénomène qui double tous les jours (ce qui n& #39;est plus le cas de la crise actuelle, hein ! ) 2/7
Chaque nouveau jour rajoute un point sur le graphique beaucoup plus haut que les précédents. Les valeurs sur l& #39;axe vertical (les ordonnées) augmentent énormément et cela "écrase" les premiers points (ils s& #39;emblent être sur une horizontale) 3/7
Une représentation exponentielle de ce type rend toute analyse difficile ! (on voit juste que ça augmente)
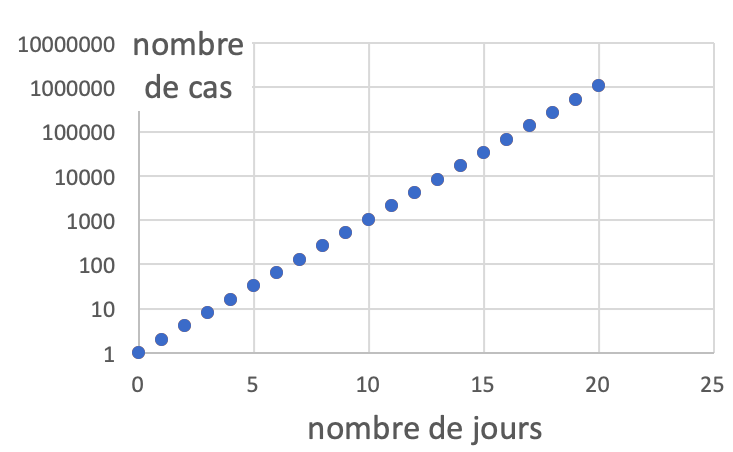
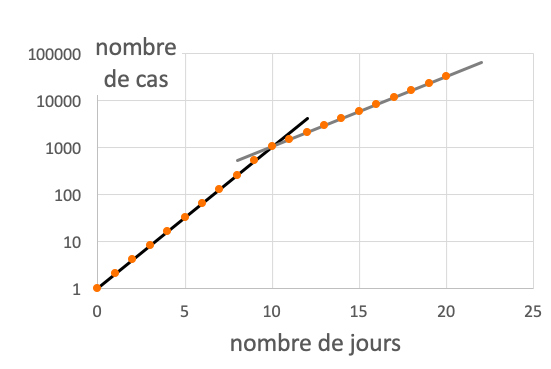
On change donc l& #39;échelle des ordonnées pour une échelle logarithmique 4/7
On change donc l& #39;échelle des ordonnées pour une échelle logarithmique 4/7
Une telle représentation permet de voir l& #39;ensemble des données et (surtout) l& #39;évolution de celles-ci 5/7
