Read on Twitter
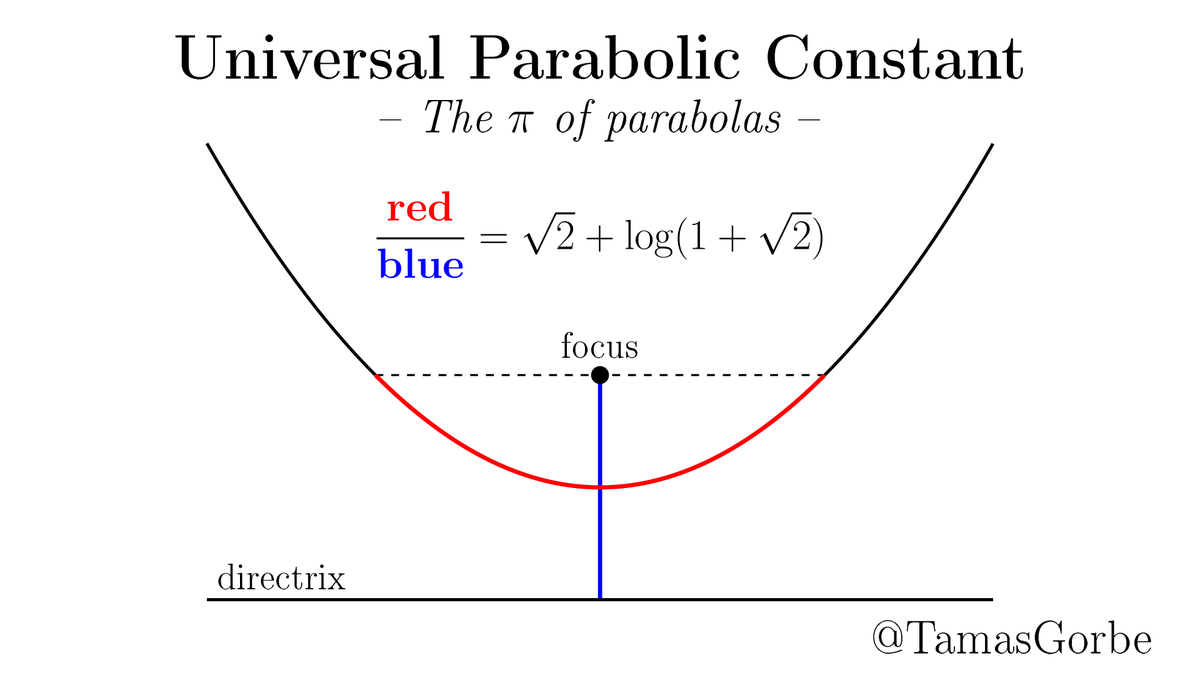
Everyone knows that all circles are similar. But did you know that all parabolas are similar?
The ratio of the red parabolic arc length and the blue focal parameter is
√2 + log(1+√2) = 2.29558...
for any parabola. This is the universal parabolic constant, the “π of parabolas”.
The ratio of the red parabolic arc length and the blue focal parameter is
√2 + log(1+√2) = 2.29558...
for any parabola. This is the universal parabolic constant, the “π of parabolas”.
The fact that “There is only one true parabola” is shown in this @standupmaths video the last 20 seconds of which is pure nightmare fuel 
The universal parabolic constant P = √2 + log(1+√2) is a transcendental number.
Proof. If P was algebraic, then so would P–√2 = log(1+√2) and by the Lindemann-Weierstrass theorem exp(P–√2) = 1+√2 would be transcendental, which it isn't.
Proof. If P was algebraic, then so would P–√2 = log(1+√2) and by the Lindemann-Weierstrass theorem exp(P–√2) = 1+√2 would be transcendental, which it isn't.
And I haven’t even mentioned the craziest connection yet... currently rendering a video demonstrating that.. watch this space
We're randomly dropping points in a 6×6 square with uniform distribution. What's the average distance from the centre?
Corners are furthest from the centre at a distance of 3√2 ≈ 4.2426, so the average must be somewhere between 0 and 3√2. But what is it?
Corners are furthest from the centre at a distance of 3√2 ≈ 4.2426, so the average must be somewhere between 0 and 3√2. But what is it?
I got 2.33 for the average distance from the centre by dropping 1,000 random points into a 6×6 square.
What could the exact value be?
What could the exact value be?
