This is a good curve. There’s a nice elementary proof – originally due to Fermat, I believe – that its only rational points are the trivial ones: https://math.stackexchange.com/q/1786448/49965  https://twitter.com/anton_hilado/status/1200443971836817412

It belongs to the family of curves parameterised by d:

y² = x³ − d²x = (x − d) x (x + d)

The rational points on this curve correspond to length-3 arithmetic progressions of rational numbers with common difference d, whose product is square.

The cool thing is that the *doubled* points (using the elliptic curve group operation) correspond to arithmetic progressions in which *every* term is square: https://mathoverflow.net/q/247407/8217 

A *congruent number* is a positive rational number that is the area of a right-angled triangle whose side lengths are also rational.

Recognising congruent numbers is a famous old problem.

It was basically solved by Jerold Tunnell in 1983, using these elliptic curves.

But the proof that Tunnell’s method works relies on the Birch/Swinnerton-Dyer conjecture, which is still unproven: it’s one of the Clay Institute’s $1m Millennium Problems.

https://en.wikipedia.org/wiki/Tunnell%27s_theorem

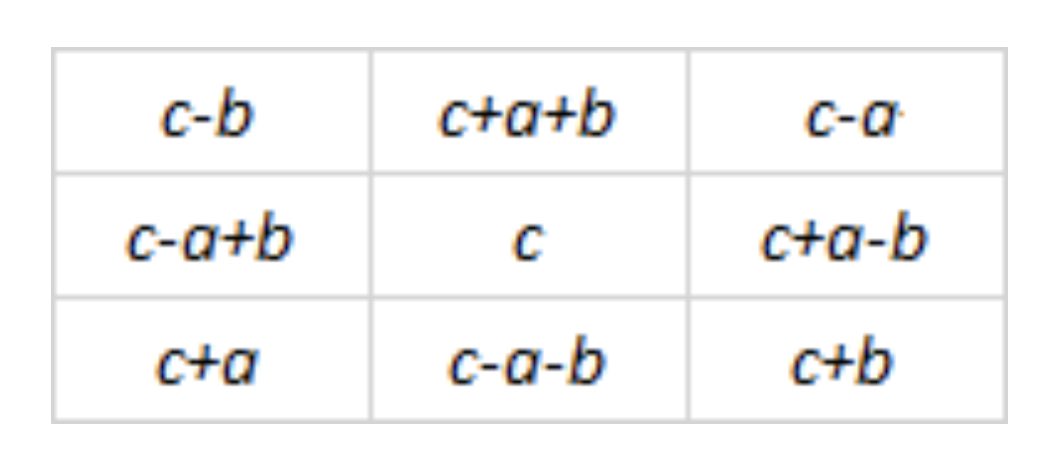
It’s also related to the notorious “Parker Square” problem: is there a 3×3 magic square all of whose entries are square numbers?

The numbers in a 3×3 magic square can be rearranged to form three arithmetic progressions with the same common difference, that are themselves in arithmetic progression.

In other words, every 3×3 magic square has this form. Édouard Lucas discovered this in the 1890s.

So an equivalent question is: can you find a number d, and three doubled rational points on the elliptic curve

y² = x³ − d²x

whose x coordinates are in arithmetic progression?

Obviously no one can, or it wouldn’t be an open problem. My guess is that it’s impossible, but we don’t know how to prove that.

Without the “doubled” part, it’s definitely possible: https://projecteuclid.org/download/pdf_1/euclid.rmjm/1320787690

I’m sure I read a paper proving that it’s impossible on curves of rank 1, using a terrifying height calculation, but I can’t remember the title or the author so I’m having trouble finding it now.

You might think that being able to construct an infinite family of these arithmetic progressions is helpful. Can’t we just construct lots of them, and look for one that consists of doubled points?

Unfortunately they’re constructed in such a way that none of them ever do!

Ah, I’ve found the paper I mentioned.

https://reader.elsevier.com/reader/sd/pii/S0022314X99924307?token=53B5D4342B95095E03CFDA59C6ABBEE0B852DF2F4213CB20F45B4F61977CF22381506D481F7E58C6309C133AC58D0C49

It actually proves something stronger than I said: it proves that no rank-1 subgroup contains an arithmetic progression.