1/ A tweetorial on false positives & transposing the conditional!
Or why interpreting type 1 error can be so confusing.
This is a common topic that overlaps in medical testing, data reporting, and statistical hypothesis tests (NHST).
Or why interpreting type 1 error can be so confusing.
This is a common topic that overlaps in medical testing, data reporting, and statistical hypothesis tests (NHST).
2/ Lets start with some basic terms!
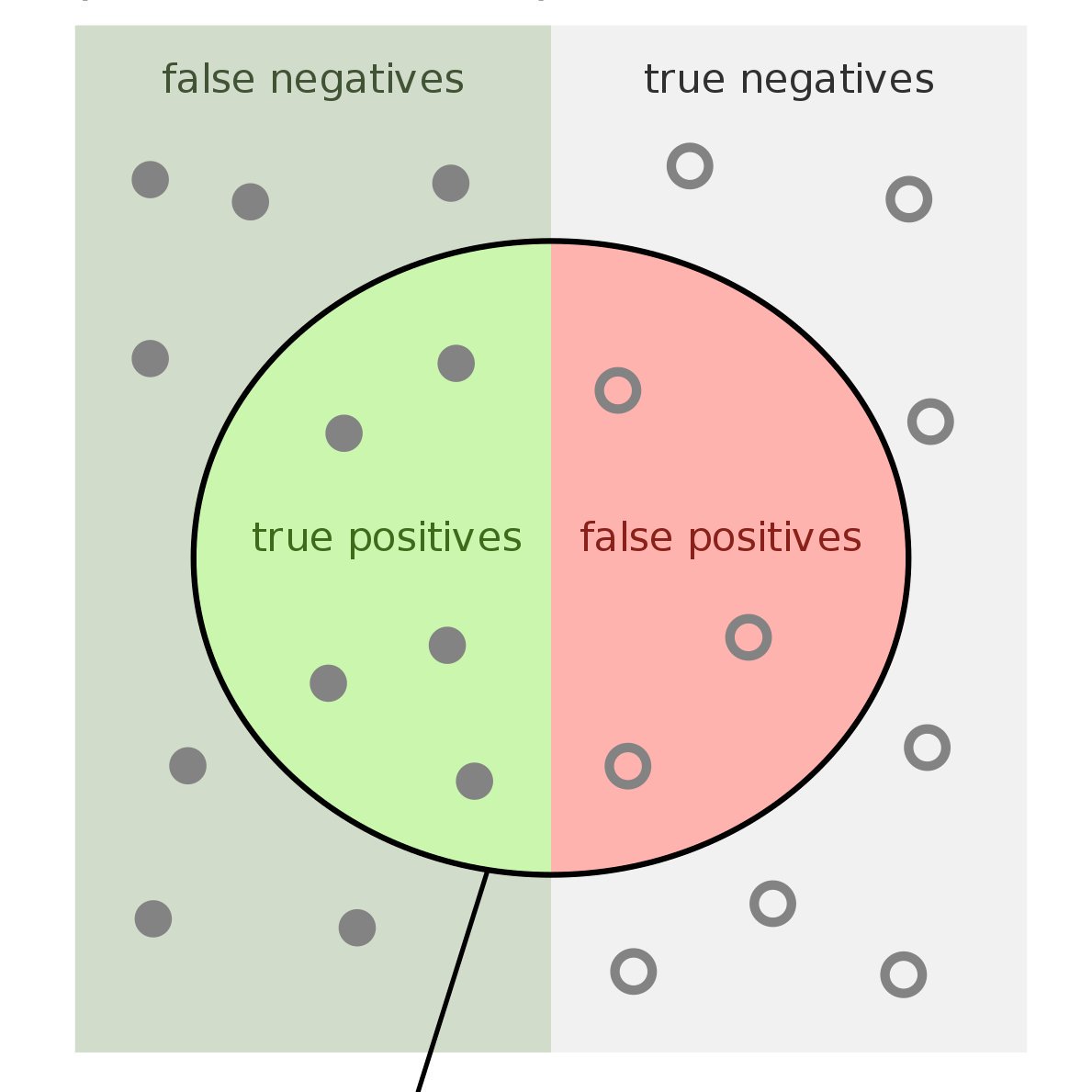
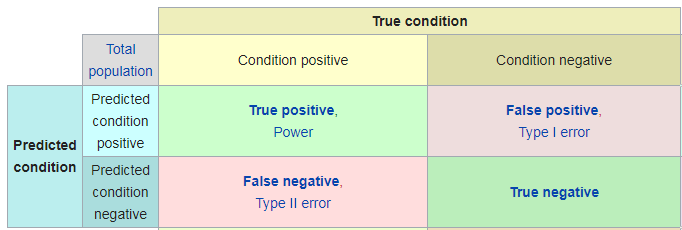
In binary classification, say for medical test results, their are 4 basic categories.
True positive
True negative
False positive
False negative
In binary classification, say for medical test results, their are 4 basic categories.
True positive
True negative
False positive
False negative
3/ We are interested in the False positive.
A false positive medical test result is when a patient DOES NOT have a condition, but the test (predicted condition) is Positive. See the table below.
A false positive medical test result is when a patient DOES NOT have a condition, but the test (predicted condition) is Positive. See the table below.
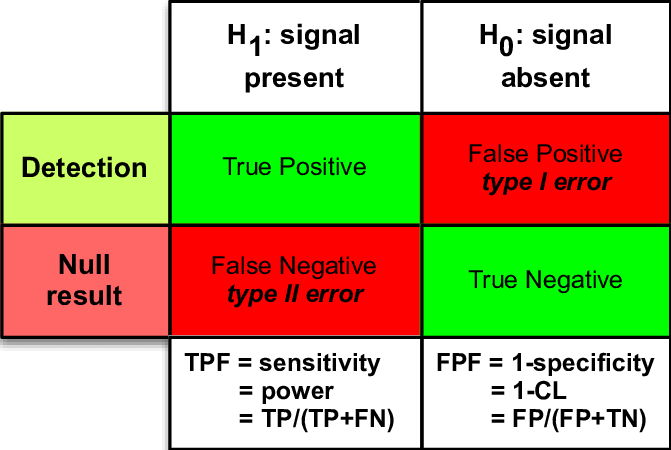
4/ A False Positive in statistical hypothesis testing is when the null hypothesis (H0) is true, but the test has a result compatible with the alternative hypothesis (H1).
In the table below, this is like detecting a signal, when no signal is present.
In the table below, this is like detecting a signal, when no signal is present.
5/ In fairy tales, a False Positive is also known as a False Alarm. Its the story of the boy who cries wolf, when no wolves are present.
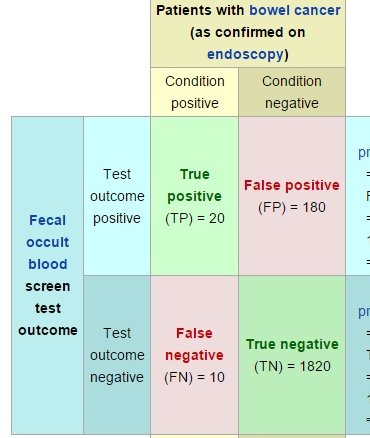
6/ Its important to note the a False Positive is a *category*.
By itself, a False Positive *is not* a fraction, or a probability, or a percentage, or a rate. It is only a count.
Below is an example of a study, where 180 test results were counted as False Positives.
By itself, a False Positive *is not* a fraction, or a probability, or a percentage, or a rate. It is only a count.
Below is an example of a study, where 180 test results were counted as False Positives.
7/ Unsurprisingly, False Positives (FP) & False Negatives (FN) are considered Errors.
In the 1920s, the statisticians Neyman and Pearson identified these possible errors of NHST, and creatively decided to label them as "Type 1 Errors" (FP) and "Type 2 Errors" (FN).
In the 1920s, the statisticians Neyman and Pearson identified these possible errors of NHST, and creatively decided to label them as "Type 1 Errors" (FP) and "Type 2 Errors" (FN).
8/ Mathematically, "Type 1 error rates" are basically a ratio of False Positives divided by the Total # of Negatives:
FP / (FP + TN)
Even though "Type 1 errors" (count) is not same as "Type 1 error rate" (ratio), we often use the terms interchangeably.
Its so confusing!
FP / (FP + TN)
Even though "Type 1 errors" (count) is not same as "Type 1 error rate" (ratio), we often use the terms interchangeably.
Its so confusing!
9/ Type 1 error rate can also be expressed as a probability (α):
Prob(FP | H0 true): If the null hypothesis is true, it& #39;s the probability of falsely rejecting it.
Prob(FP | condition absent): If the condition/disease is absent, it& #39;s the probability of falsely diagnosing it.
Prob(FP | H0 true): If the null hypothesis is true, it& #39;s the probability of falsely rejecting it.
Prob(FP | condition absent): If the condition/disease is absent, it& #39;s the probability of falsely diagnosing it.
10/ OK! Following so far? Hopefully this has set the stage for the fun part of the tweetorial.
Because now we dive into the rabbit hole!
Because now we dive into the rabbit hole!
11/ Scenario 1: Lets say we have a positive medical test result, but are unsure if a disease is truly present. We want to know if the test result is wrong, i.e. a False Positive or Type 1 Error.
How do we determine the chances that this a false positive? What do we calculate?
How do we determine the chances that this a false positive? What do we calculate?
12/ The correct answer is "Other".
We want to know: Given a positive result, what is probability that the condition is absent. Prob(Condition absent | Pos Test).
But Type 1 Error Rate (α) is Prob(FP | Condition absent), the inverse (transposed conditional) of our question!
We want to know: Given a positive result, what is probability that the condition is absent. Prob(Condition absent | Pos Test).
But Type 1 Error Rate (α) is Prob(FP | Condition absent), the inverse (transposed conditional) of our question!
13/ So in our scenario, the "Type 1 error rate" (α) does not help us determine the probability of having a false positive.
Or, to be doubly confusing: in our scenario the "Type 1 Error Rate" (α) does not help us determine the probability of having a "Type 1 Error".
Or, to be doubly confusing: in our scenario the "Type 1 Error Rate" (α) does not help us determine the probability of having a "Type 1 Error".
14/ Now, to be triply confusing: "Type 1 Error" is often used interchangeably with "Type 1 Error Rate". As such, the the "probability of Type 1 error rate" (α), is often defined just as "the probability of type 1 error".
Got that?
Got that?
15/ Yet the (α) defined as "probability of a Type 1 error" is still the conditional inverse of our attempt in the previously stated scenario to calculate the "probability of a false positive" or "probability of a Type 1 error".
Are you confused? Im feeling pretty confused.
Are you confused? Im feeling pretty confused.
16/ What is the solution out of this semantic and transposed conditional quagmire?
The best advice I& #39;ve heard is this:
1) use conditional statements for probability
2) limit usage of the phrase "type 1 error" to study design
3) avoid pos/neg labels for non-binary test results
The best advice I& #39;ve heard is this:
1) use conditional statements for probability
2) limit usage of the phrase "type 1 error" to study design
3) avoid pos/neg labels for non-binary test results
17/ Scenario 1: We have a positive test result, but are unsure if the disease/condition is truly present.
Confusing Q: Is this a false positive or type 1 error?
Good Q: Given the positive test result, what is the probability that the condition is absent?
Confusing Q: Is this a false positive or type 1 error?
Good Q: Given the positive test result, what is the probability that the condition is absent?
18/ Scenario 2: A study has made a new discovery, and we want determine the chances it is wrong.
Wrong Q: What is the chance of type 1 error rate (α)?
Confusing Q: What is the chance of a false positive?
Good Q: Given the study results, what is prob the discovery is false?
Wrong Q: What is the chance of type 1 error rate (α)?
Confusing Q: What is the chance of a false positive?
Good Q: Given the study results, what is prob the discovery is false?
19/ When discussing False Positives, always keep in mind
i) am i discussing the "category" and counts?
ii) am i discussing rates & probability?
iii) for probability questions, what is the conditional order?
i) am i discussing the "category" and counts?
ii) am i discussing rates & probability?
iii) for probability questions, what is the conditional order?
20/ End
I hope this thread has been helpful introduction to the topic. Feel free to post corrections or comments.
I hope this thread has been helpful introduction to the topic. Feel free to post corrections or comments.

 Read on Twitter
Read on Twitter