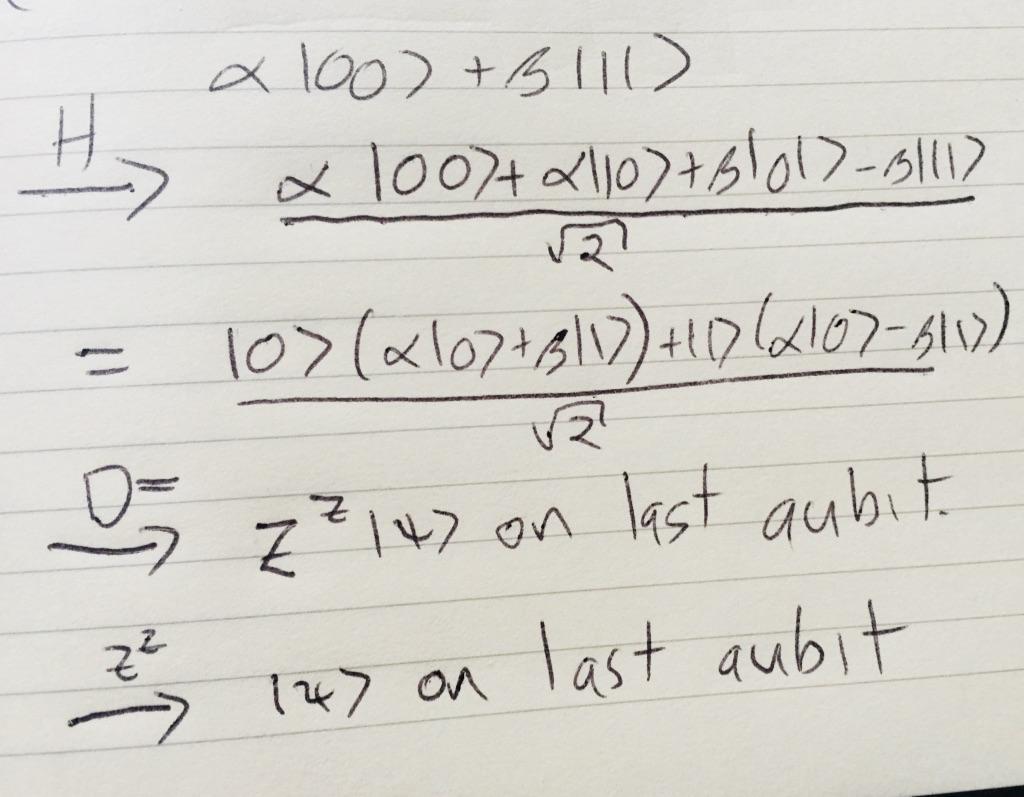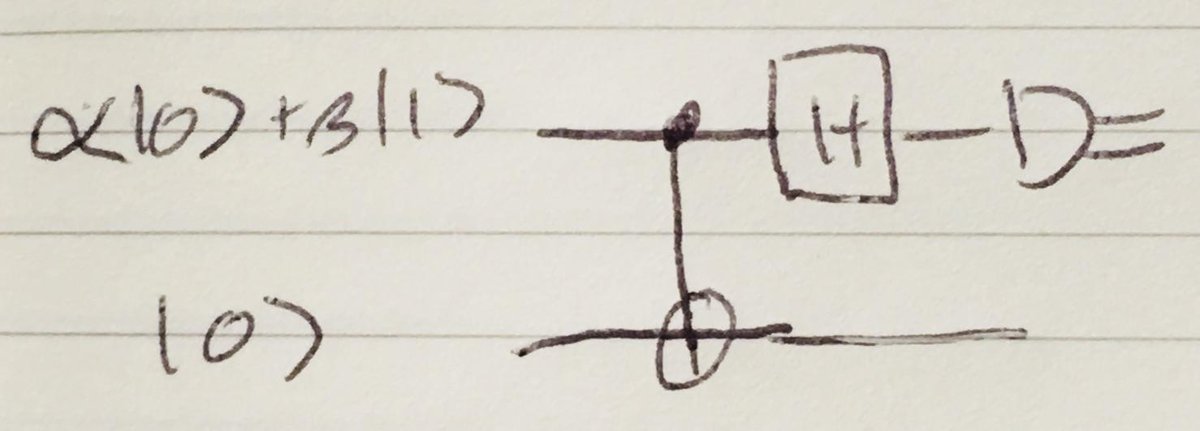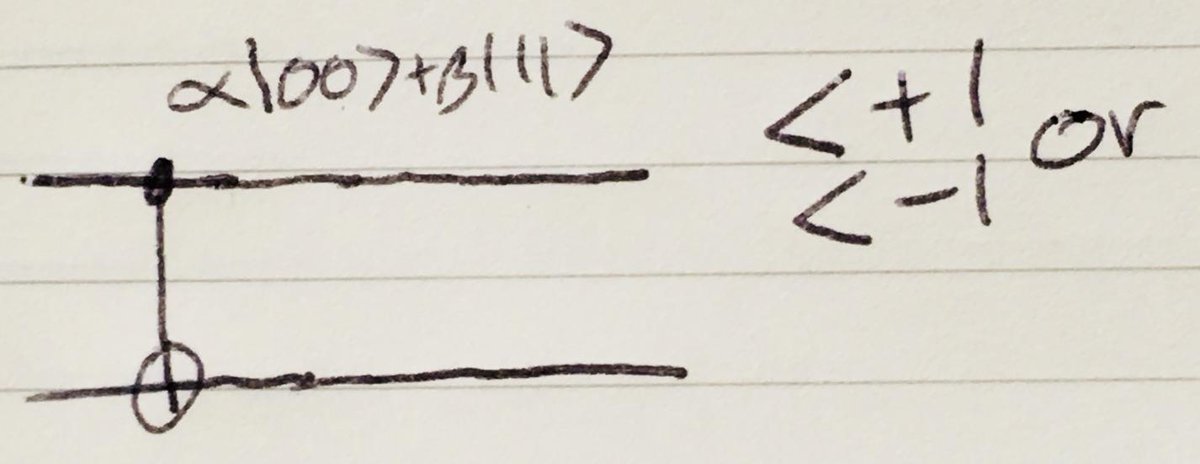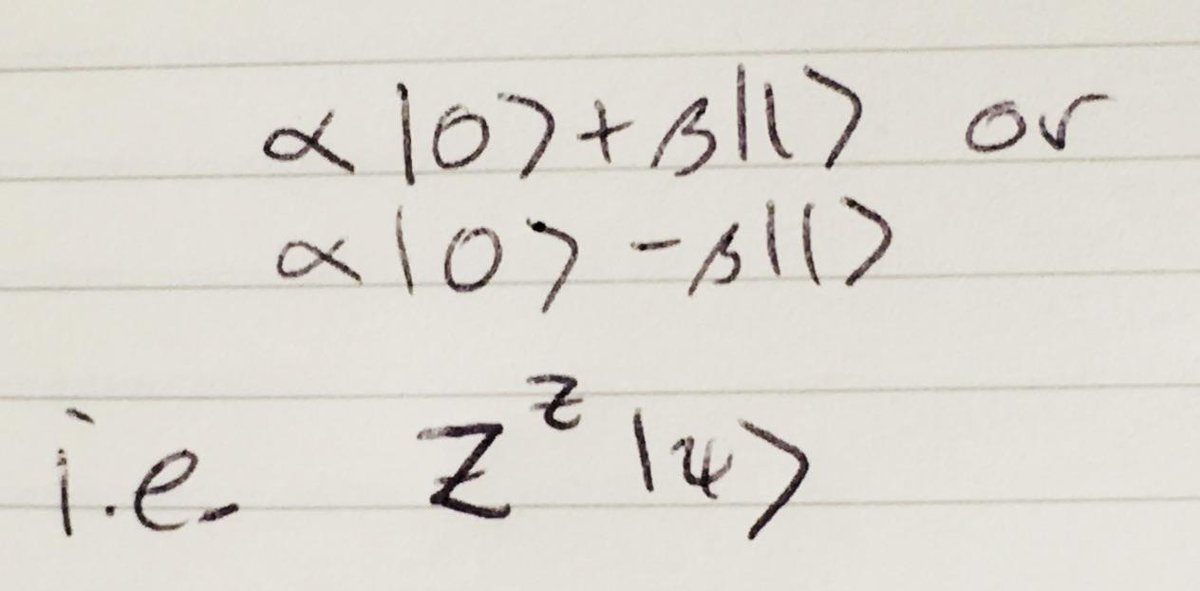Had some fun this afternoon re-analyzing the circuit for quantum teleportation. Here's a proof I found that the circuit works.

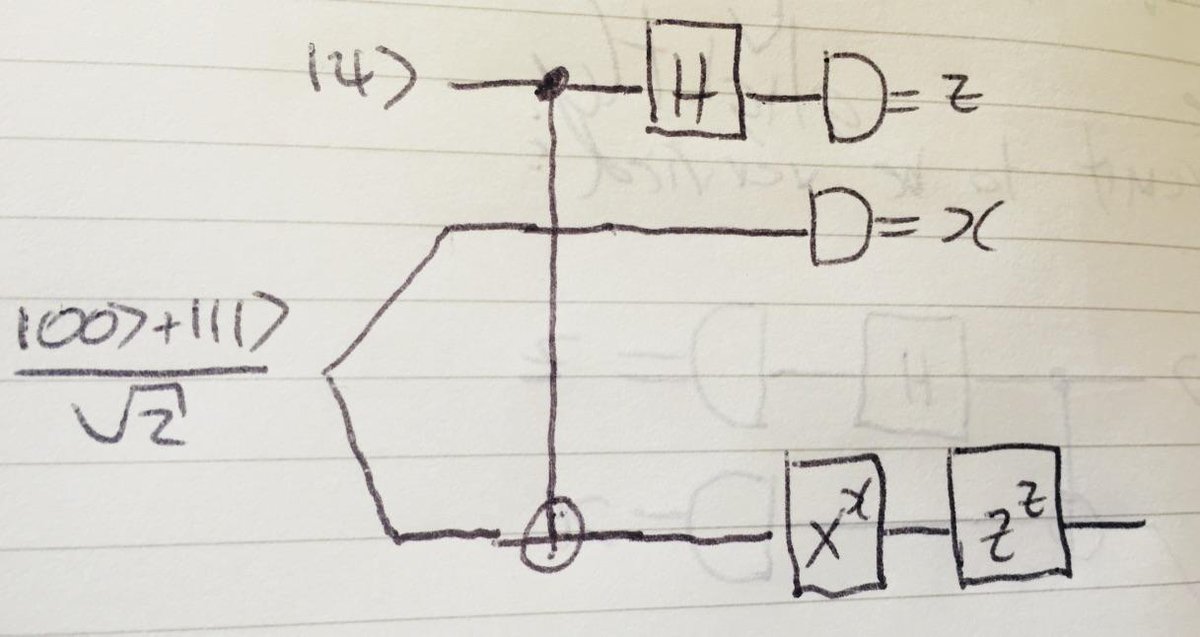
The circuit to be verified: top two qubits are Alice's, including the state psi to be teleported. Bottom qubit is Bob's - want to show it outputs psi.

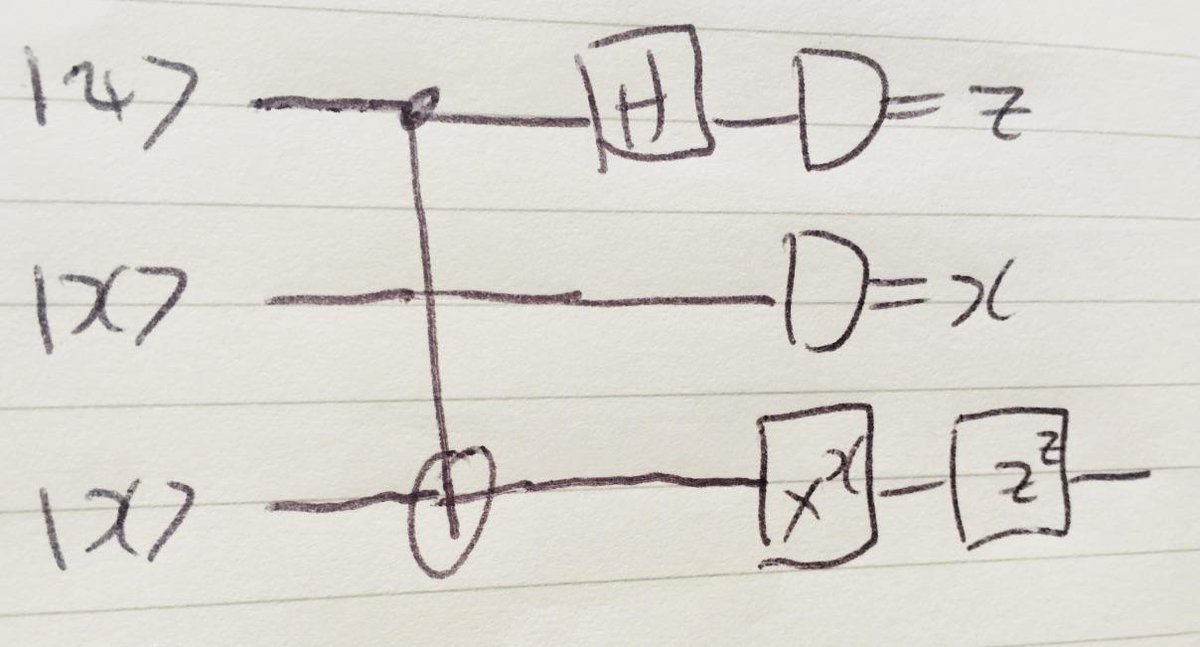
The shared state (|00>+|11>)/sqrt 2 is symmetric, so the original circuit is equivalent to one where we move the CNOT target to the third qubit:

We can measure the second qubit as early as we like, without changing the output from the circuit. In fact, we can do the measurement right at the beginning of the protocol, giving:

We can now ignore the second qubit - it no longer has any impact on the output we're interested in. We can also commute the X^x past the CNOT target, to get:

I don't know of any way of computing the output here, except to do the algebra:

Of course, we could have just done the algebra for the whole 3-qubit system up front. It's really not very complicated, & that's how I've always done it in the past. But I noticed this approach a few hours ago, & rather like it. It's in some sense longer, but more elegant.

No claim that this is new! But it was new & pleasing to me, a slightly new way of seeing an old friend.

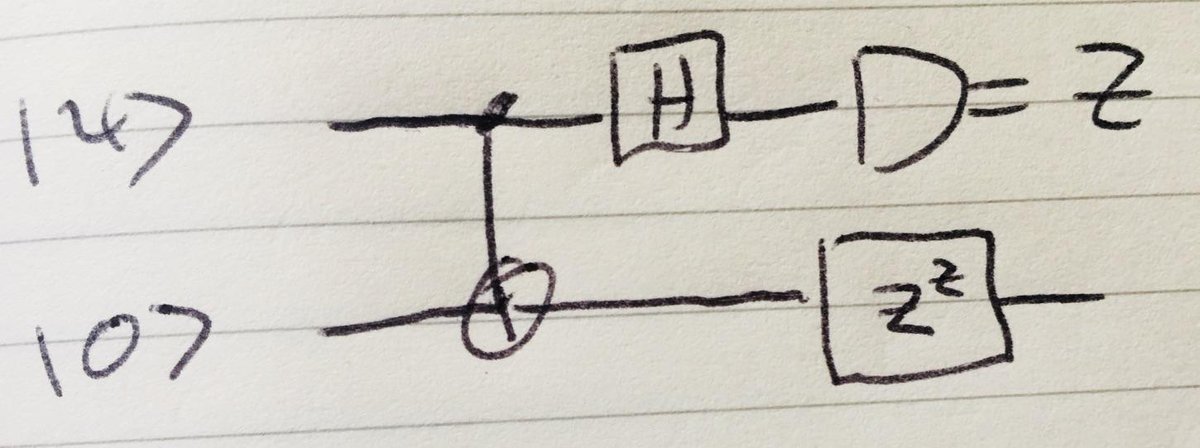
Update: In fact, it is possible to analyze the two-qubit circuit with almost no algebra. Ignoring the final Z^z gate, the main thing to analyze is this circuit:

We run the state through the CNOT, and then Hadamard + measurement is equivalent to measuring in the <+| or <-| basis:

The resulting conditional states are as shown, and we can simply cancel the Z^z term:

I really like the first part of the proof: it's just a quantum one-time pad. I don't quite know how to think about the second part of the proof. Why does measuring in the |+>, |-> basis work? It's easy to prove it does, but I don't have a really good explanation for why.