1/n ) My first grad school paper, "Achieving Stable Dynamics in Neural Circuits" is out today in @PLOSCompBiol. A fun theory project with @LundqvistNeuro, Jean-Jacques Slotine (sadly not on Twitter), & @MillerLabMIT. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1007659
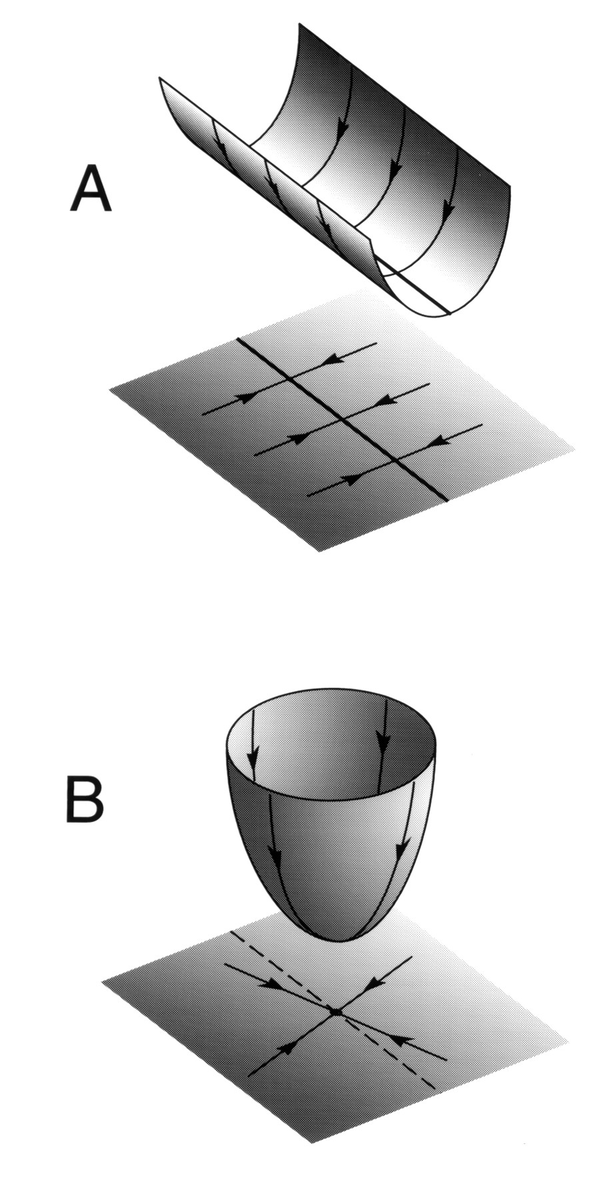
2/n) Stability in neuroscience is usually defined with respect to objects in state space, e.g lines (A) or points (B). Neural trajectories are attracted towards these objects, even in the face of small perturbations--hence, stable. Fig from Seung, 1996 https://www.pnas.org/content/93/23/13339
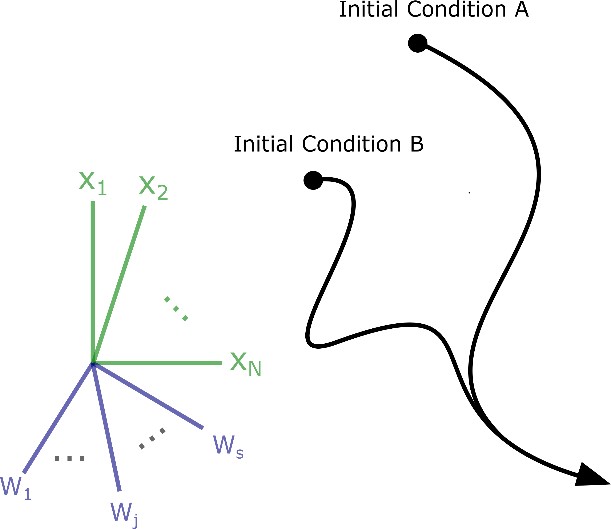
3/n) But this definition of stability doesn't really work for systems receiving external inputs (e.g brains), because there may not be any fixed objects in state space to be attracted towards. So how should stability be defined for systems with time-varying, external input?
4/n) One way to address this question is to ask when neural trajectories will be stable towards each other, even if they are time-varying and complex. In other words, separate the idea of stability from the idea of asymptotic behavior (like sitting on a fixed point or line).
5/n) Contraction analysis (a mathematical framework developed in the control theory literature) gives conditions for achieving these types of stable dynamics. Systems with this property are said to be contracting. http://web.mit.edu/nsl/www/preprints/contraction.pdf
6/n) When we applied contraction analysis to neural networks, we found that a variety of known synaptic mechanisms give rise to overall contracting dynamics, including-but-not-limited-to: inhibitory Hebbian plasticity, excitatory anti-Hebbian plasticity and E-I balance. How?
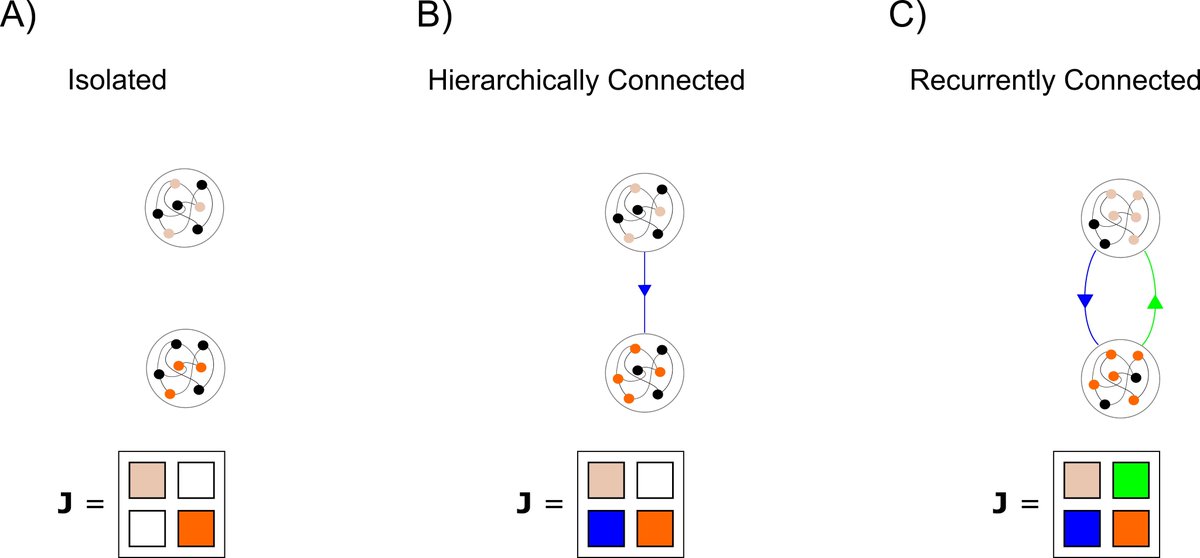
7/n) It turns out that two isolated, contracting systems can be combined in ways that are known to preserve contraction of the overall system. We exploited this 'Lego ™' property to prove our results, by imagining synapses and neurons to be two interacting subsystems...
8/n) ...and then deriving synaptic dynamics that would correspond to these known, stability-preserving combination types. We were surprised and happy to find synaptic dynamics that already had names in the literature!
n-1 /n) One limitation of our work is that it only applies to rate-based networks (for now). Our next steps are figuring out how to apply this framework to spiking neural networks, and also developing techniques for measuring stability in real neural data.
n/n) Finally, thanks to @LundqvistNeuro for being a great collaborator and @MillerLabMIT for being an ever-supportive, awesome advisor. Also thanks to the anonymous reviewers who gave excellent criticisms and helped take this work to the next level.

 Read on Twitter
Read on Twitter